import numpy as np
from scipy.optimize import minimize
from scipy.stats import norm
import matplotlib.pyplot as plt
from numpy.linalg import cholesky, solve
from scipy.spatial.distance import pdist, squareform, cdist
#1. Die KrigingRegressor-Klasse (erweitert um Expected Improvement)
# Für dieses Beispiel vereinfachen wir die Implementierung,
# um den Fokus auf Expected Improvement zu legen.
# Eine vollständige Implementierung wäre umfangreicher.
class KrigingRegressor:
def __init__(self, theta=None, p=2.0, eps=np.sqrt(np.spacing(1))):
self.theta = theta if theta is not None else np.array([1.0]) # Aktivitätshyperparameter
self.p = p # Glattheitsparameter, hier fest auf 2.0 (sqeuclidean)
self.eps = eps # Nugget-Effekt für numerische Stabilität
self.X_train = None
self.y_train = None
self.mu_hat = None
self.sigma_hat_sq = None
self.Psi = None
self.U = None # Cholesky-Faktor
def _build_psi_matrix(self, X_data, w=None):
"""Berechnet die Korrelationsmatrix Psi mit gewichteter quadrierter euklidischer Distanz.
Args:
X_data (np.ndarray): Eingabedaten-Matrix
w (np.ndarray, optional): Gewichtungsparameter (theta)
Returns:
np.ndarray: Korrelationsmatrix Psi
"""
if w is None:
w = self.theta
D = squareform(pdist(X_data, metric='sqeuclidean', w=w))
Psi = np.exp(-D)
# Nugget-Effekt für numerische Stabilität - verwende die Anzahl der Datenpunkte
n_points = X_data.shape[0] # Anzahl der Zeilen (Datenpunkte)
Psi += np.multiply(np.eye(n_points), self.eps)
return Psi
def _build_psi_vector(self, X_predict, X_train, w=None):
# Berechnet den Korrelationsvektor psi zwischen Vorhersage- und Trainingspunkten
if w is None:
w = self.theta
D = cdist(X_predict, X_train, metric='sqeuclidean', w=w)
psi = np.exp(-D)
return psi.T # Transponieren, um n x m oder n x 1 zu erhalten
def fit(self, X_train, y_train):
"""Trainiert das Kriging-Modell auf den gegebenen Daten.
Args:
X_train (np.ndarray): Trainings-Eingabedaten
y_train (np.ndarray): Trainings-Zielwerte
"""
self.X_train = X_train
self.y_train = y_train
n = self.X_train.shape[0] # Anzahl der Datenpunkte, nicht die gesamte Shape
# Numerisch stabile Berechnung der Psi-Matrix
self.Psi = self._build_psi_matrix(self.X_train)
# Cholesky-Zerlegung für effiziente Inversion
# U ist der obere Dreiecksfaktor (Transponierte des unteren)
try:
self.U = cholesky(self.Psi).T
except np.linalg.LinAlgError:
print("Cholesky-Zerlegung fehlgeschlagen, Matrix ist nicht positiv definit.")
# Fallback oder Fehlerbehandlung, z.B. größeren Nugget-Term verwenden
self.Psi = self._build_psi_matrix(self.X_train, self.theta + 1e-6)
self.U = cholesky(self.Psi).T
# Berechnung von mu_hat (geschätzter globaler Mittelwert)
one_vec = np.ones((n, 1))
# solve(U, solve(U.T, vec)) ist äquivalent zu inv(Psi) @ vec unter Verwendung von Cholesky
self.mu_hat = (one_vec.T @ solve(self.U, solve(self.U.T, self.y_train))) / \
(one_vec.T @ solve(self.U, solve(self.U.T, one_vec)))
self.mu_hat = self.mu_hat.item() # Extrahiere Skalarwert
# Berechnung von sigma_hat_sq (geschätzte Prozessvarianz)
self.sigma_hat_sq = ((self.y_train - one_vec * self.mu_hat).T @ \
solve(self.U, solve(self.U.T, self.y_train - one_vec * self.mu_hat))) / n
self.sigma_hat_sq = self.sigma_hat_sq.item()
def predict(self, X_predict):
"""Vorhersage für neue Datenpunkte.
Args:
X_predict (np.ndarray): Eingabedaten für Vorhersage
Returns:
np.ndarray: Vorhergesagte Werte
"""
if self.X_train is None or self.y_train is None:
raise ValueError("Modell muss zuerst mit fit() trainiert werden.")
m = X_predict.shape[0] # Anzahl der Vorhersagepunkte
n = self.X_train.shape[0] # Anzahl der Trainingspunkte
one_vec_m = np.ones((m, 1))
one_vec_n = np.ones((n, 1))
psi_vec = self._build_psi_vector(X_predict, self.X_train)
# BLUP-Formel: y_hat(x) = mu_hat + psi.T @ inv(Psi) @ (y_train - 1 * mu_hat)
f_predict = self.mu_hat * one_vec_m + \
psi_vec.T @ solve(self.U, solve(self.U.T, self.y_train - one_vec_n * self.mu_hat))
return f_predict.flatten()
def predict_variance(self, X_predict):
if self.X_train is None or self.y_train is None:
raise ValueError("Modell muss zuerst mit fit() trainiert werden.")
psi_vec = self._build_psi_vector(X_predict, self.X_train)
# Geschätzter Fehler (Varianz) s^2(x)
# s^2(x) = sigma_hat_sq * (1 - psi.T @ inv(Psi) @ psi)
s_sq = self.sigma_hat_sq * (1 - np.diag(psi_vec.T @ solve(self.U, solve(self.U.T, psi_vec))))
# Sicherstellen, dass die Varianz nicht negativ ist (numerische Stabilität)
s_sq[s_sq < 1e-10] = 1e-10
return s_sq.flatten()
def expected_improvement(self, x_cand, y_min_current):
# x_cand sollte ein 2D-Array sein, auch für 1D-Probleme: np.array([[x]])
mu_cand = self.predict(x_cand) # y_hat(x)
s_cand = np.sqrt(self.predict_variance(x_cand)) # s(x)
# Handhabung für s_cand == 0 (bereits beprobte Punkte)
# Vermeidet Division durch Null und gibt EI = 0 zurück
ei_values = np.zeros_like(mu_cand)
# Indizes, wo s_cand > 0 ist
positive_s_indices = s_cand > 1e-10
if np.any(positive_s_indices):
s_pos = s_cand[positive_s_indices]
mu_pos = mu_cand[positive_s_indices]
Z = (y_min_current - mu_pos) / s_pos
# Formel für Expected Improvement
# EI = (ymin - y_hat) * Phi(Z) + s * phi(Z)
ei_values[positive_s_indices] = (y_min_current - mu_pos) * norm.cdf(Z) + s_pos * norm.pdf(Z)
# Sicherstellen, dass EI nicht negativ wird (numerische Stabilität)
ei_values[ei_values < 0] = 0
return ei_values
def _neg_expected_improvement(self, x_cand_flat, y_min_current):
# Wrapper für die Optimierung, erwartet flaches x_cand
x_cand = np.array(x_cand_flat).reshape(1, -1) # Formatiere zu 2D
ei = self.expected_improvement(x_cand, y_min_current)
# Minimierungsziel ist negatives EI
return -ei # EI ist hier ein Skalar, daher 69 Lernmodul: Kriging Projekt mit Expected Improvement
Dies ist ein erweitertes Lernmodul, das auf dem “Lernmodul: Kriging Projekt” aufbaut und “Expected Improvement” (EI) als Infill-Kriterium verwendet.
69.1 Einleitung
Das vorhergehende “Lernmodul: Kriging Projekt” hat die Grundlagen der sequenziellen Optimierung mittels Kriging-Surrogatmodellen etabliert. Dabei wurde die nächste Evaluierungsstelle im Designraum einfach durch die Minimierung der Surrogatmodellvorhersage gewählt – ein Ansatz, der hauptsächlich auf Exploitation abzielt, also der Ausnutzung vielversprechender Regionen. In der Praxis ist es jedoch entscheidend, ein Gleichgewicht zwischen Exploitation und Exploration (Erkundung unsicherer Regionen) zu finden, insbesondere bei teuren Black-Box-Funktionen.
Dieses Lernmodul erweitert den sequenziellen Optimierungsablauf, indem es Expected Improvement (EI) als Infill-Kriterium integriert. EI ist eine der einflussreichsten und am weitesten verbreiteten Methoden in der bayesianischen Optimierung, da sie Exploitation und Exploration auf elegante Weise in einem einzigen Kriterium vereint.
69.2 1. Die KrigingRegressor-Klasse (Erweiterung)
Die KrigingRegressor-Klasse, die bereits für die Berechnung der Korrelationsmatrizen, die Maximum-Likelihood-Schätzung der Hyperparameter (\(\hat{\mu}\), \(\hat{\sigma}^2\), \(\vec{\theta}\)) und die Vorhersagefunktion (predict) verwendet wurde, wird um eine Methode zur Berechnung des Expected Improvement erweitert.
EI nutzt sowohl die Vorhersage des Modells (\(\hat{y}(\vec{x})\)) als auch die Unsicherheit der Vorhersage (Varianz \(\hat{s}^2(\vec{x})\)), die Kriging-Modelle bereitstellen können. Die Fähigkeit von Kriging, ein Maß für die Unsicherheit zu liefern, ist ein entscheidender Vorteil gegenüber einfacheren Surrogatmodellen wie Polynomen.
69.3 2. Die Black-Box-Funktion f(x) (Wiederholung)
Wie im vorherigen Modul simuliert die Black-Box-Funktion f(x) ein teures oder undurchsichtiges System. Für dieses Beispiel verwenden wir weiterhin eine analytische Funktion, um die Prinzipien zu demonstrieren.
69.4 3. Initialer Stichprobenplan X (Wiederholung)
Der Prozess beginnt mit einem initialen Stichprobenplan, der typischerweise mittels Latin Hypercube Sampling (LHS) erstellt wird. LHS ist eine raumfüllende Technik, die sicherstellt, dass der Eingaberaum effizient und gleichmäßig erkundet wird, was eine gute Ausgangsbasis für das Kriging-Modell bietet.
69.5 4. Sequenzieller Optimierungsablauf mit Expected Improvement
Der iterative Prozess der sequenziellen Optimierung wird wie folgt angepasst:
- Initialisierung: Ein initialer Stichprobenplan
Xwird erstellt und die Black-Box-Funktionfan diesen Punkten evaluiert, um die Beobachtungenyzu erhalten. - Kriging-Modell anpassen: Das Kriging-Modell wird mit den gesammelten Daten (
X,y) angepasst. Hierbei werden die Hyperparameter (insbesondere \(\vec{\theta}\)) mittels Maximum-Likelihood-Schätzung optimiert. - Expected Improvement (EI) berechnen: Für eine Vielzahl von Kandidatenpunkten im Designraum wird das Expected Improvement berechnet. EI quantifiziert den erwarteten Gewinn, wenn man die Black-Box an einem bestimmten Punkt evaluiert, im Vergleich zum besten bisher beobachteten Wert (
y_min). Die Formel für EI lautet: \[ E[I(\vec{x})] = (\hat{y}_{min} - \hat{y}(\vec{x})) \cdot \Phi\left(\frac{\hat{y}_{min} - \hat{y}(\vec{x})}{\hat{s}(\vec{x})}\right) + \hat{s}(\vec{x}) \cdot \phi\left(\frac{\hat{y}_{min} - \hat{y}(\vec{x})}{\hat{s}(\vec{x})}\right) \] wobei:- \(\hat{y}_{min}\) der beste bisher beobachtete Funktionswert ist.
- \(\hat{y}(\vec{x})\) die Kriging-Vorhersage am Punkt \(\vec{x}\) ist.
- \(\hat{s}(\vec{x})\) die geschätzte Standardabweichung (Wurzel aus der Varianz) der Vorhersage am Punkt \(\vec{x}\) ist.
- \(\Phi\) die kumulative Verteilungsfunktion (CDF) und \(\phi\) die Wahrscheinlichkeitsdichtefunktion (PDF) der Standardnormalverteilung sind.
- Ein Wert von 0 wird zurückgegeben, wenn \(\hat{s}(\vec{x}) = 0\) (d.h. an einem bereits beprobten Punkt ist die Unsicherheit null).
- Nächsten Infill-Punkt auswählen: Anstatt den Punkt mit der besten Vorhersage zu wählen, wird der Punkt ausgewählt, der das Expected Improvement maximiert. Da die meisten Optimierungsalgorithmen auf Minimierung ausgelegt sind, wird üblicherweise die negative Expected Improvement-Funktion minimiert.
- Evaluierung und Aktualisierung: Der ausgewählte Punkt wird der teuren Black-Box-Funktion übergeben, die Beobachtung wird zum Trainingsdatensatz hinzugefügt, und der Prozess wird iteriert.
Vorteile von EI: * Automatisches Gleichgewicht: EI balanciert Exploration und Exploitation automatisch, ohne manuelle Gewichtungsparameter. * Theoretische Fundierung: Es hat eine starke theoretische Rechtfertigung aus der Entscheidungstheorie. * Effiziente Optimierung: Die differenzierbare Natur von EI macht es für gradientenbasierte Optimierungsalgorithmen geeignet. * Globale Konvergenz: Eine Maximierung von EI führt letztendlich zum globalen Optimum, da EI an beprobten Punkten auf null fällt, was die Suche in ungesampelte, unsichere oder vielversprechende Bereiche lenkt.
69.6 Der entsprechende Python-Code:
Für dieses Modul simulieren wir eine KrigingRegressor-Klasse, die die notwendigen fit, predict und expected_improvement Methoden enthält. Der Fokus des Codes liegt auf dem angepassten sequenziellen Optimierungsablauf.
70 2. Die Black-Box-Funktion f(x)
Beispiel: Sinusfunktion mit hinzugefügtem (optionalem) Rauschen
def f(x_val):
# Standardisierung von x_val von zu [0, 2*pi] für die Sinusfunktion
# Annahme, dass die Optimierung in^k durchgeführt wird und die Blackbox
# intern die Skalierung handhabt.
# Für dieses Beispiel behalten wir die direkte Nutzung der Sinusfunktion.
return np.sin(x_val) # + np.random.normal(0, 0.05) # Optional: Rauschen hinzufügen#3. Initialer Stichprobenplan X (Latin Hypercube Sampling)
Implementierung eines einfachen LHS für 1D für das Beispiel
def latin_hypercube_sampling(n_points, n_dims, lower_bound=0, upper_bound=1):
"""Erstellt Latin Hypercube Samples im gegebenen Bereich.
Args:
n_points (int): Anzahl der zu generierenden Punkte
n_dims (int): Anzahl der Dimensionen
lower_bound (float): Untere Grenze des Suchraums
upper_bound (float): Obere Grenze des Suchraums
Returns:
np.ndarray: Array der Form (n_points, n_dims) mit LHS-Samples
"""
points = np.zeros((n_points, n_dims))
for i in range(n_dims):
# Erstelle n_points gleichmäßige Intervalle
bins = np.linspace(lower_bound, upper_bound, n_points + 1)
# Berechne die Intervallbreite
interval_width = (upper_bound - lower_bound) / n_points
# Generiere zufällige Offsets innerhalb jedes Intervalls
random_offsets = np.random.rand(n_points) * interval_width
# Setze Punkte in jedes Intervall
points[:, i] = bins[:-1] + random_offsets
# Permutiere die Punkte für jede Dimension (wichtig für LHS)
np.random.shuffle(points[:, i])
return points70.1 Hauptskript für die sequentielle Optimierung
n_initial_points = 5 # Anzahl der initialen Stichprobenpunkte
n_infill_points = 10 # Anzahl der hinzuzufügenden Infill-Punkte
n_dimensions = 1 # Problem-Dimension (für sin(x) ist k=1)
# 1. Initialisierung: Initialer Stichprobenplan und Evaluierung
# x-Werte im Bereich für die Optimierung
X_initial = latin_hypercube_sampling(n_initial_points, n_dimensions)
# y-Werte im Bereich [0, 2*pi] für die Sinusfunktion
# Wir skalieren X_initial für die f-Funktion, wenn f in einem anderen Bereich definiert ist.
# Für Sin(x) verwenden wir direkt X_initial skaliert auf [0, 2*pi]
X_train_scaled = X_initial * (2 * np.pi) # Skalierung für sin(x)
y_train = np.array([f(x_val) for x_val in X_train_scaled]).reshape(-1, 1)
X_train = X_initial # Behalte X_train in für KrigingRegressor
# Initialisiere KrigingRegressor
kriging_model = KrigingRegressor()
kriging_model.fit(X_train, y_train)
# Speicher für die Visualisierung
all_X = X_train.copy()
all_y = y_train.copy()
# Range für die Vorhersage/Visualisierung
x_plot = np.linspace(0, 1, 100).reshape(-1, 1) # Im standardisierten Bereich
x_plot_scaled = x_plot * (2 * np.pi) # Skalieren für die wahre Funktion
plt.figure(figsize=(12, 8))
plt.plot(x_plot_scaled, f(x_plot_scaled), 'grey', linestyle='--', label='Wahre Sinusfunktion')
plt.plot(all_X * (2 * np.pi), all_y, 'bo', markersize=8, label='Messungen (Initial)')
plt.title('Sequenzielle Optimierung mit Expected Improvement')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.legend()
plt.show()
# Sequenzieller Optimierungsablauf
for i in range(n_infill_points):
print(f"\n--- Iteration {i+1}: Suche Infill-Punkt mittels Expected Improvement ---")
# Besten bisher beobachteten Wert finden (für Minimierungsproblem)
y_min_current = np.min(all_y)
print(f"Bester bisheriger Wert (y_min): {np.round(y_min_current, 4)}")
# Suchgrenzen für die Optimierung auf dem Surrogatmodell (im Einheitshyperwürfel)
# Für 1D ist es einfach
bounds = [(0, 1)] * n_dimensions
# Optimierung des Surrogatmodells zur Suche des nächsten Infill-Punktes
# Wir minimieren die negative Expected Improvement
# Starte die Suche von mehreren zufälligen Punkten, um lokale Minima zu vermeiden
num_restarts = 5
best_ei_val = -np.inf
next_x_infill = None
for _ in range(num_restarts):
# Zufälliger Startpunkt innerhalb der Grenzen
x0 = np.random.rand(n_dimensions)
res = minimize(kriging_model._neg_expected_improvement, x0,
args=(y_min_current,),
bounds=bounds,
method='L-BFGS-B') # Oder andere geeignete Methode
# EI ist der negative Wert des Ergebnisses der Minimierung
current_ei_val = -res.fun
if current_ei_val > best_ei_val:
best_ei_val = current_ei_val
next_x_infill = res.x
if next_x_infill is None:
# Fallback, falls Optimierung fehlschlägt, z.B. zufälligen Punkt wählen
next_x_infill = np.random.rand(n_dimensions)
print("Warnung: EI-Optimierung fehlgeschlagen, wähle zufälligen Punkt.")
# Stelle sicher, dass next_x_infill 2D ist für die predict-Methoden
next_x_infill_2d = next_x_infill.reshape(1, -1)
print(f"Gewählter Infill-Punkt (standardisiert): {np.round(next_x_infill, 4)}")
print(f"Geschätztes EI am Infill-Punkt: {np.round(best_ei_val, 4)}")
# Evaluierung des Infill-Punktes auf der realen Black-Box-Funktion
# Skaliere den Infill-Punkt für die f-Funktion
next_x_infill_scaled = next_x_infill * (2 * np.pi)
y_new = np.array([f(next_x_infill_scaled)]).reshape(-1, 1)
print(f"Tatsächlicher Wert am Infill-Punkt: {np.round(y_new.item(), 4)}")
# Daten zum Trainingssatz hinzufügen
all_X = np.vstack((all_X, next_x_infill_2d))
all_y = np.vstack((all_y, y_new))
# Kriging-Modell neu anpassen mit den aktualisierten Daten
kriging_model.fit(all_X, all_y)
# Visualisierung des aktuellen Zustands
plt.figure(figsize=(10, 8))
# Plot auf der ersten Y-Achse (linke Seite)
ax1 = plt.gca()
ax1.plot(x_plot_scaled, f(x_plot_scaled), 'grey', linestyle='--', label='Wahre Sinusfunktion')
ax1.plot(x_plot_scaled, kriging_model.predict(x_plot), 'orange', label='Kriging Vorhersage')
ax1.plot(all_X[:-1] * (2 * np.pi), all_y[:-1], 'bo', markersize=8, label='Messungen (bisher)')
ax1.plot(all_X[-1] * (2 * np.pi), all_y[-1], 'ro', markersize=10, label='Neuer Infill-Punkt')
ax1.set_xlabel('x')
ax1.set_ylabel('y')
ax1.grid(True)
# Plot Expected Improvement auf der zweiten Y-Achse (rechte Seite)
ax2 = ax1.twinx()
ei_values_plot = kriging_model.expected_improvement(x_plot, y_min_current)
ax2.plot(x_plot_scaled, ei_values_plot, 'g:', label='Expected Improvement (EI)')
ax2.set_ylabel('Expected Improvement', color='g')
ax2.tick_params(axis='y', labelcolor='g')
plt.title(f'Iteration {i+1}: Kriging Vorhersage und EI (y_min={np.round(y_min_current, 4)})')
# Korrekte Behandlung der Legenden von beiden Achsen
lines1, labels1 = ax1.get_legend_handles_labels()
lines2, labels2 = ax2.get_legend_handles_labels()
ax1.legend(lines1 + lines2, labels1 + labels2, loc='upper right')
plt.show()
print("\n--- Optimierung abgeschlossen ---")
print(f"Finaler bester Wert gefunden: {np.round(np.min(all_y).item(), 4)}")
print(f"Gesamtzahl der Evaluierungen: {len(all_y)}")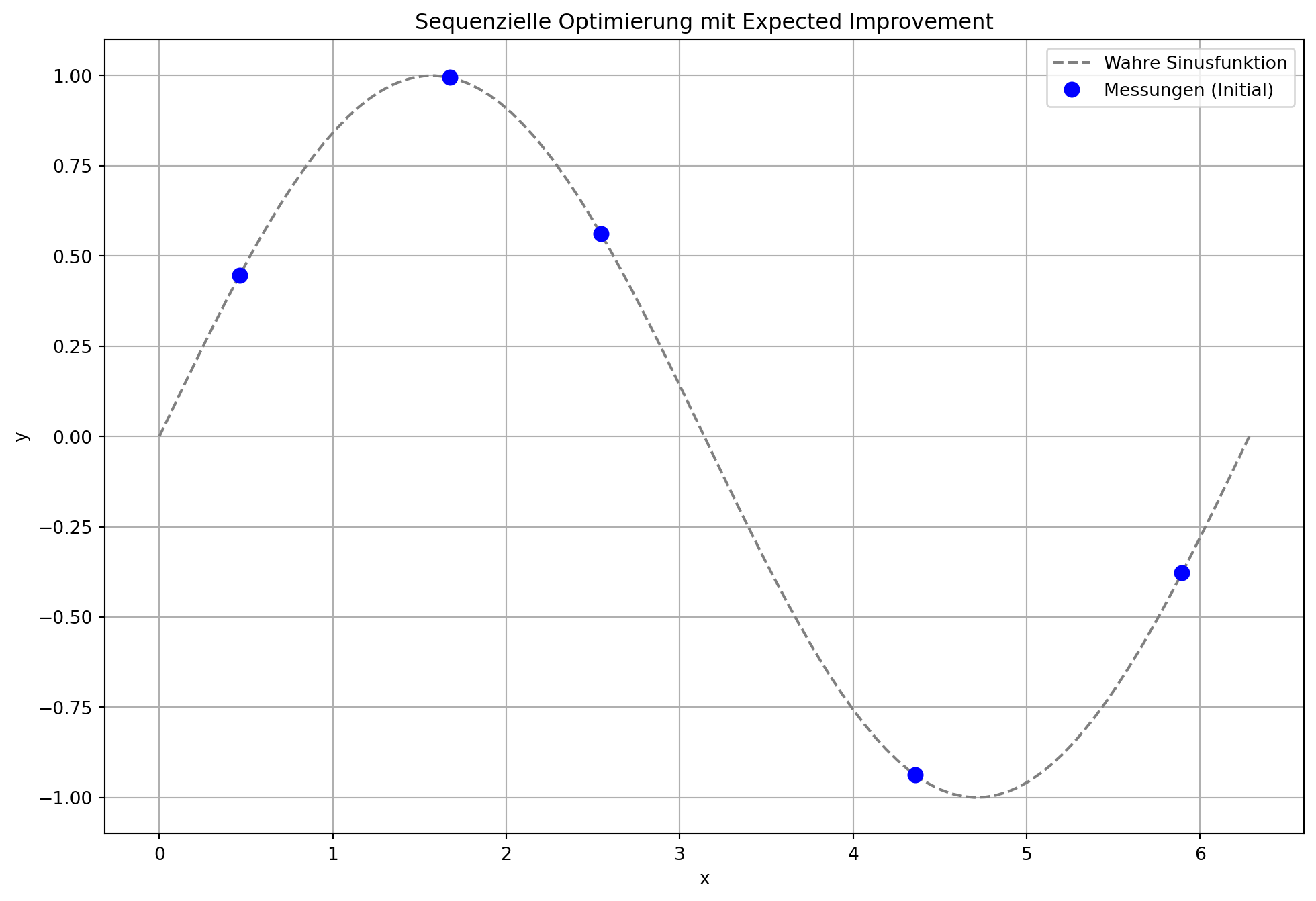
--- Iteration 1: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -0.9975
Gewählter Infill-Punkt (standardisiert): [0.7351]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: -0.9956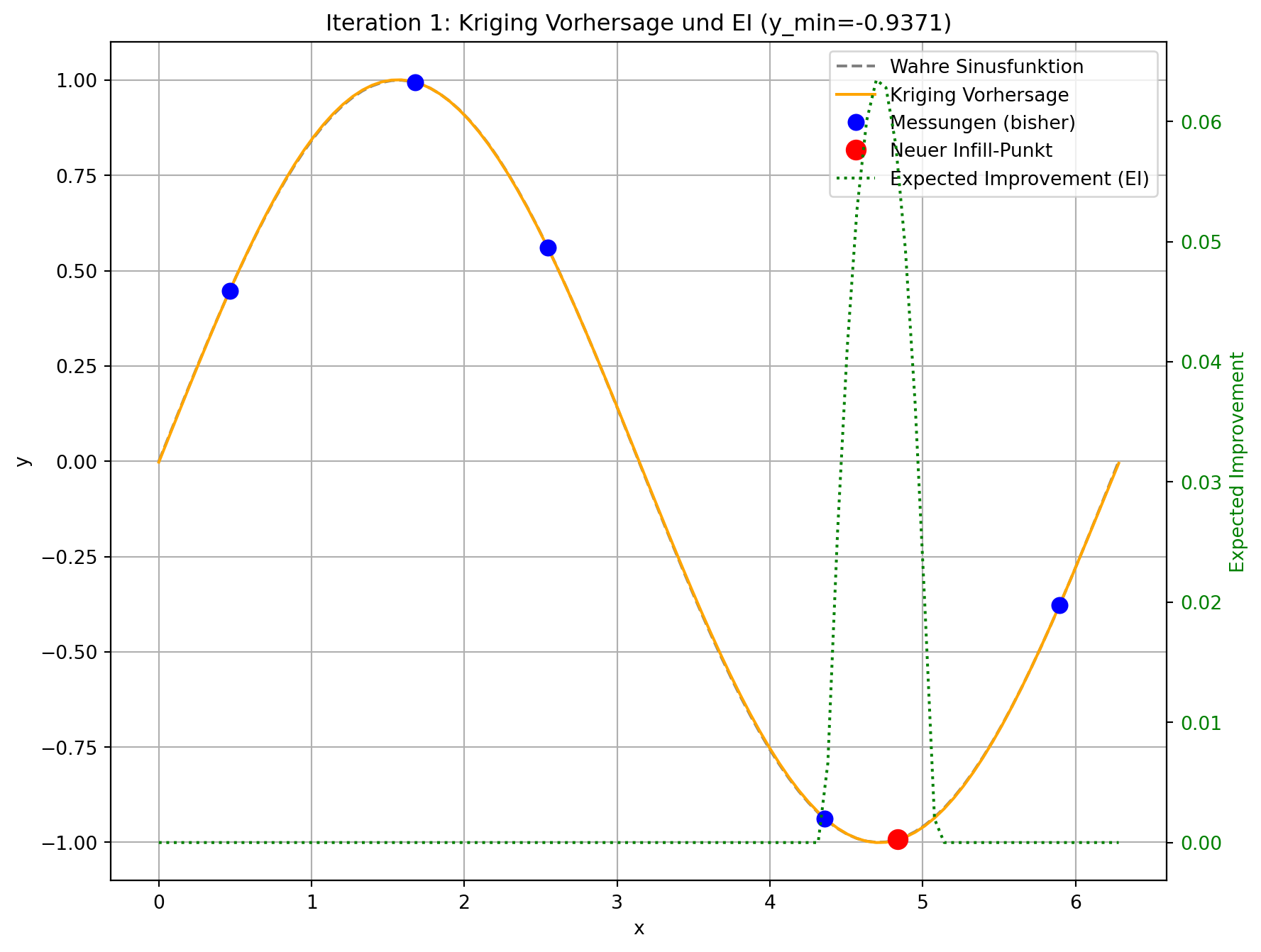
--- Iteration 2: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -0.9975
Gewählter Infill-Punkt (standardisiert): [0.162]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: 0.8509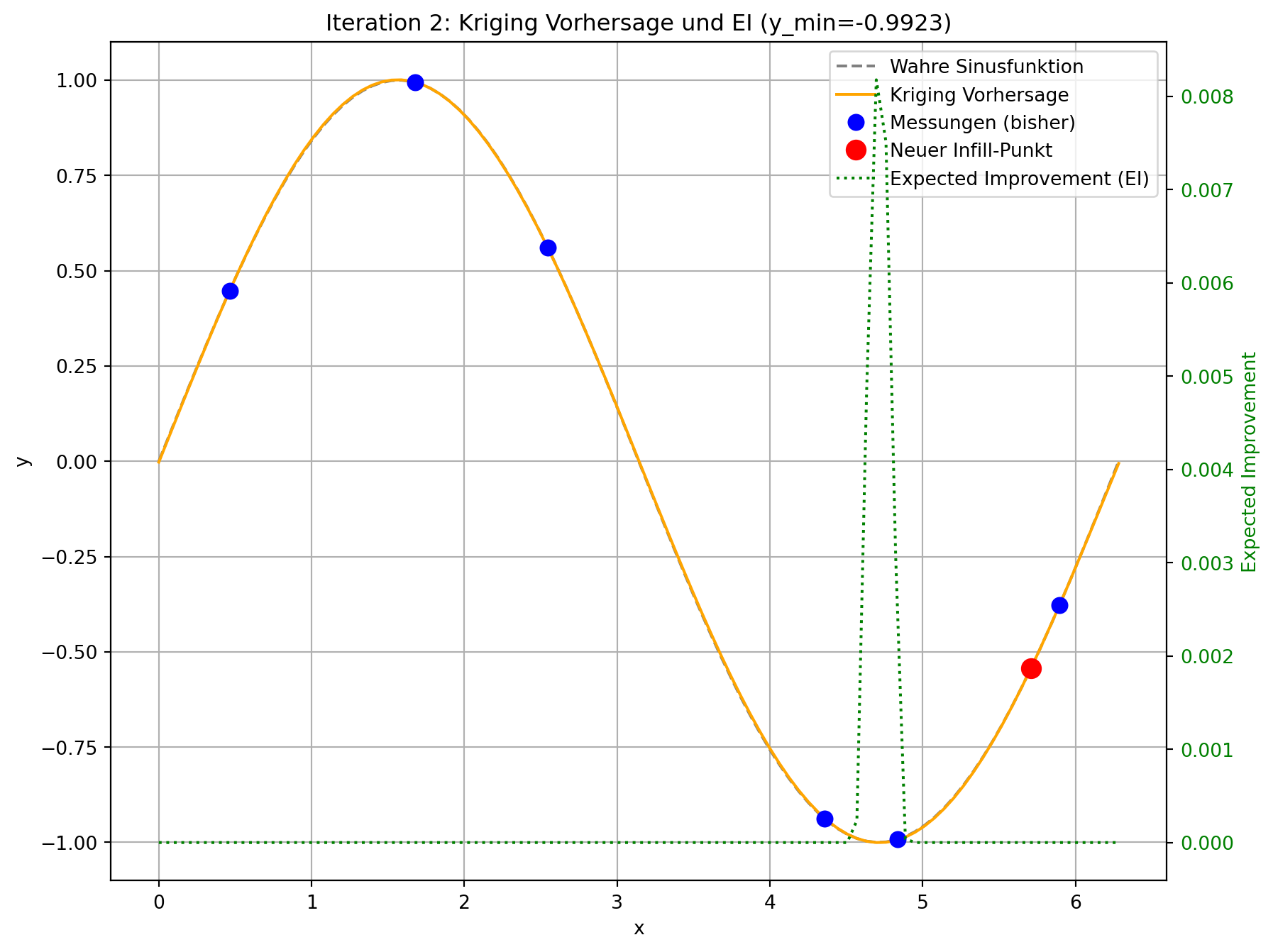
--- Iteration 3: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -0.9975
Gewählter Infill-Punkt (standardisiert): [0.7525]
Geschätztes EI am Infill-Punkt: 0.003
Tatsächlicher Wert am Infill-Punkt: -0.9999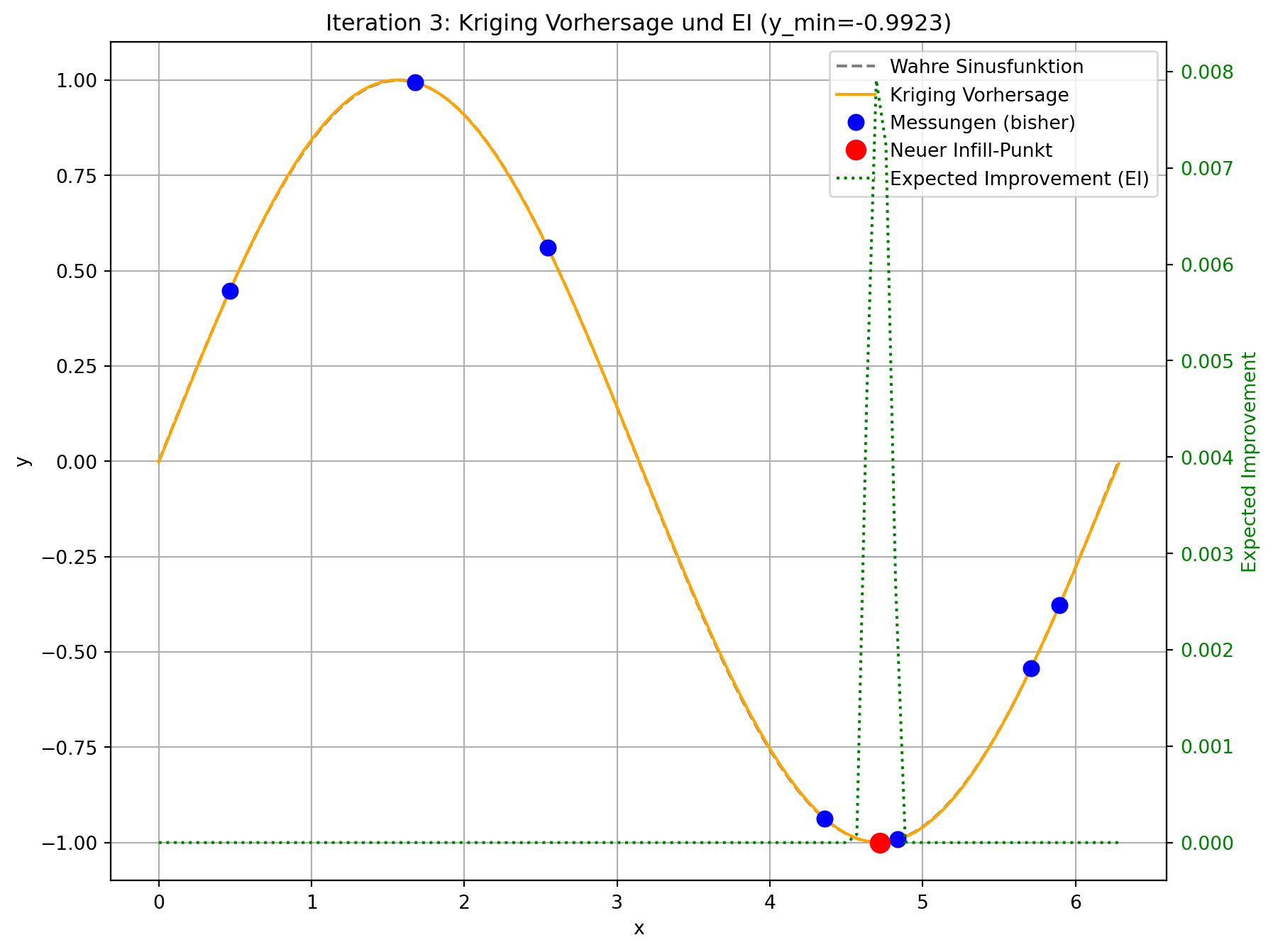
--- Iteration 4: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -0.9999
Gewählter Infill-Punkt (standardisiert): [0.6807]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: -0.9067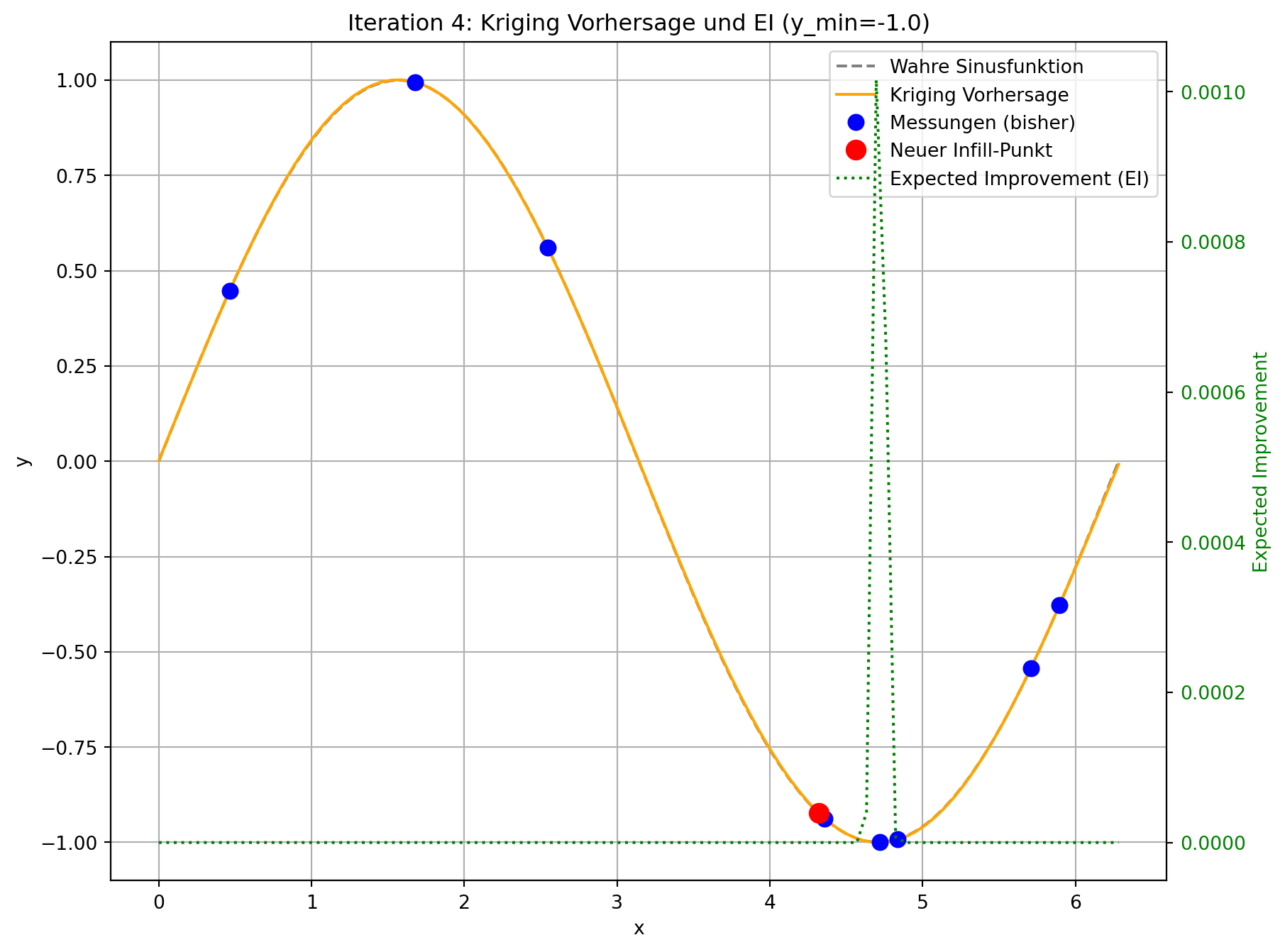
--- Iteration 5: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -0.9999
Gewählter Infill-Punkt (standardisiert): [0.84]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: -0.8442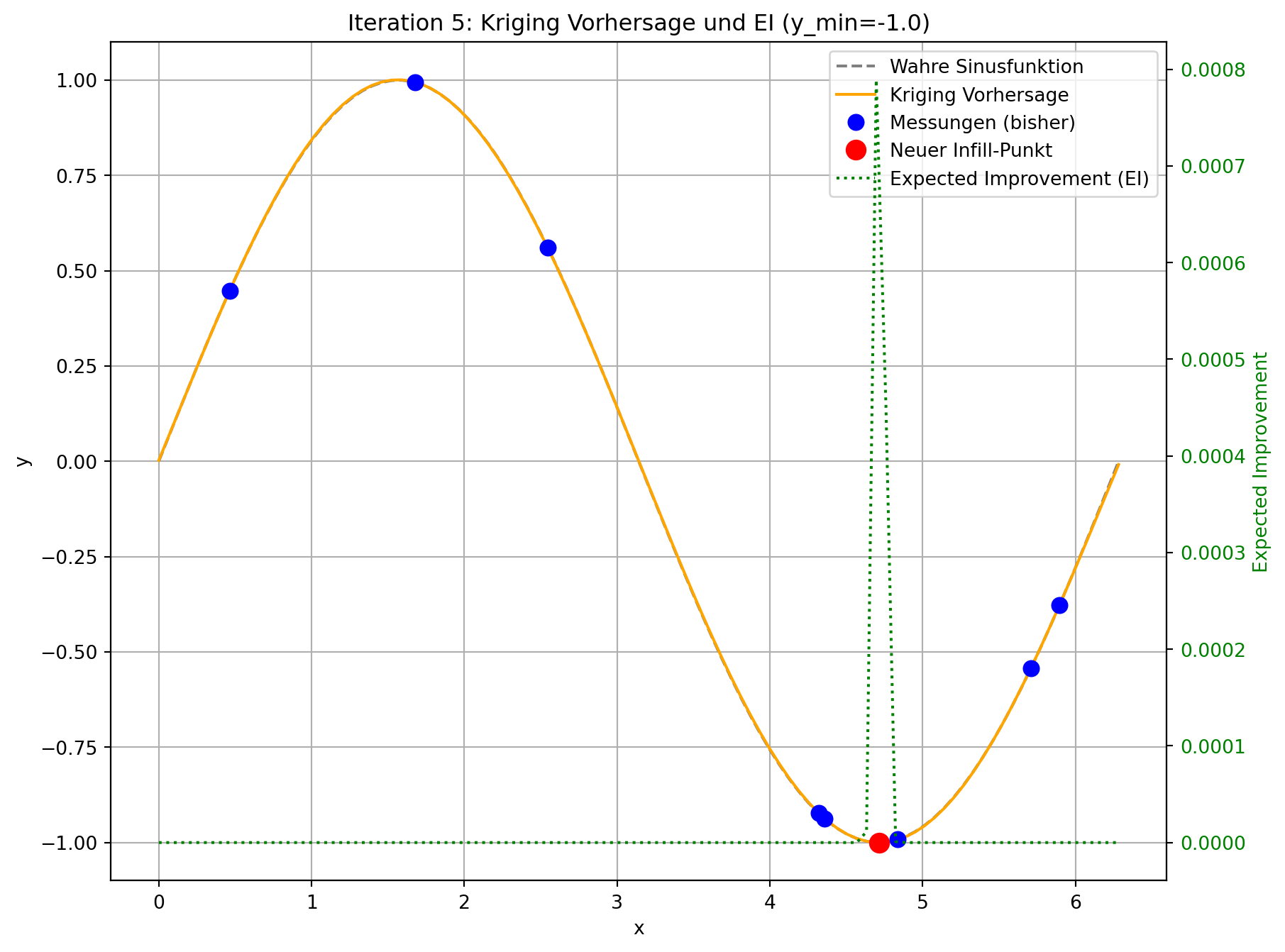
--- Iteration 6: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -0.9999
Gewählter Infill-Punkt (standardisiert): [0.7504]
Geschätztes EI am Infill-Punkt: 0.0008
Tatsächlicher Wert am Infill-Punkt: -1.0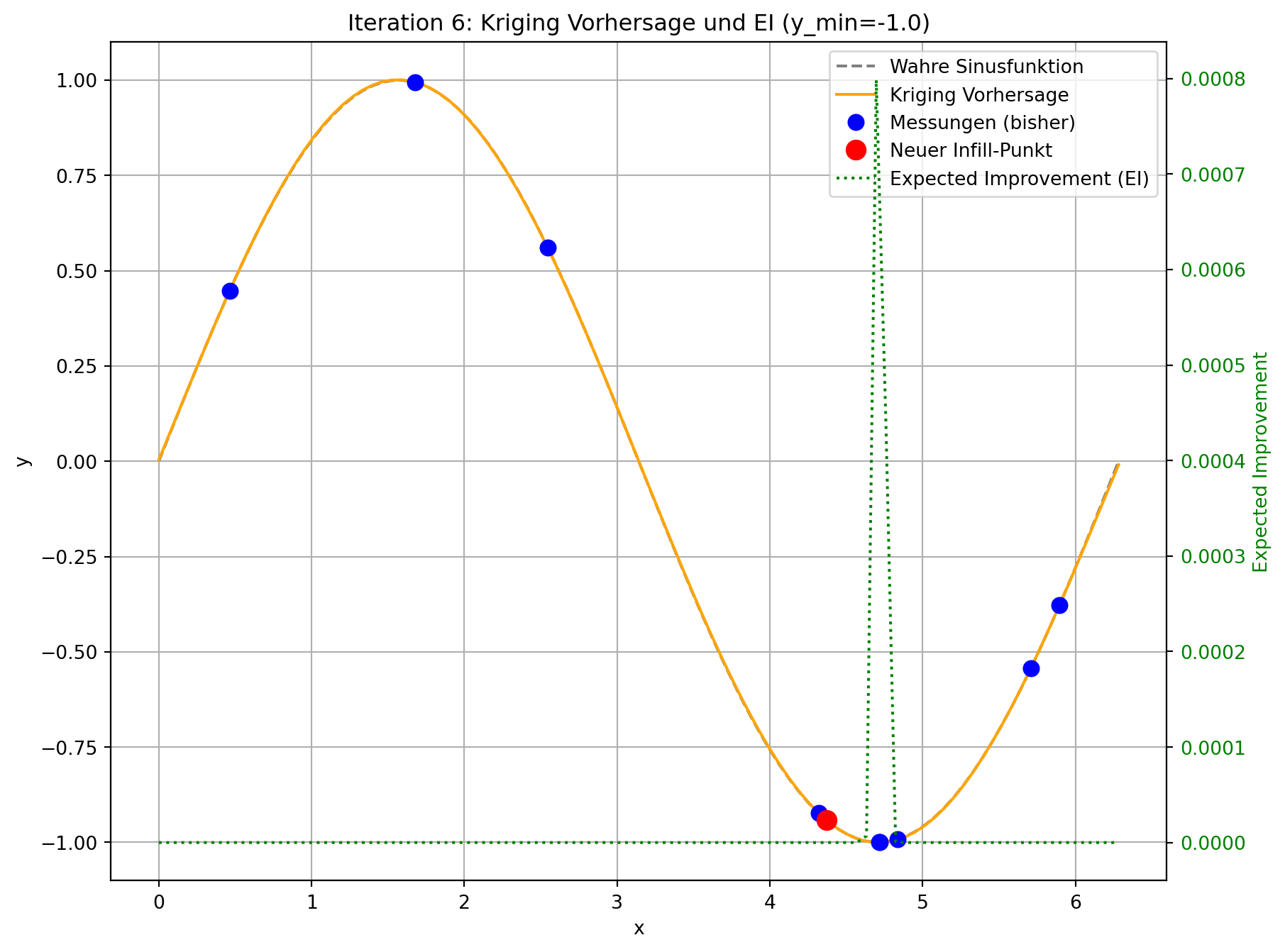
--- Iteration 7: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -1.0
Gewählter Infill-Punkt (standardisiert): [0.3469]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: 0.8202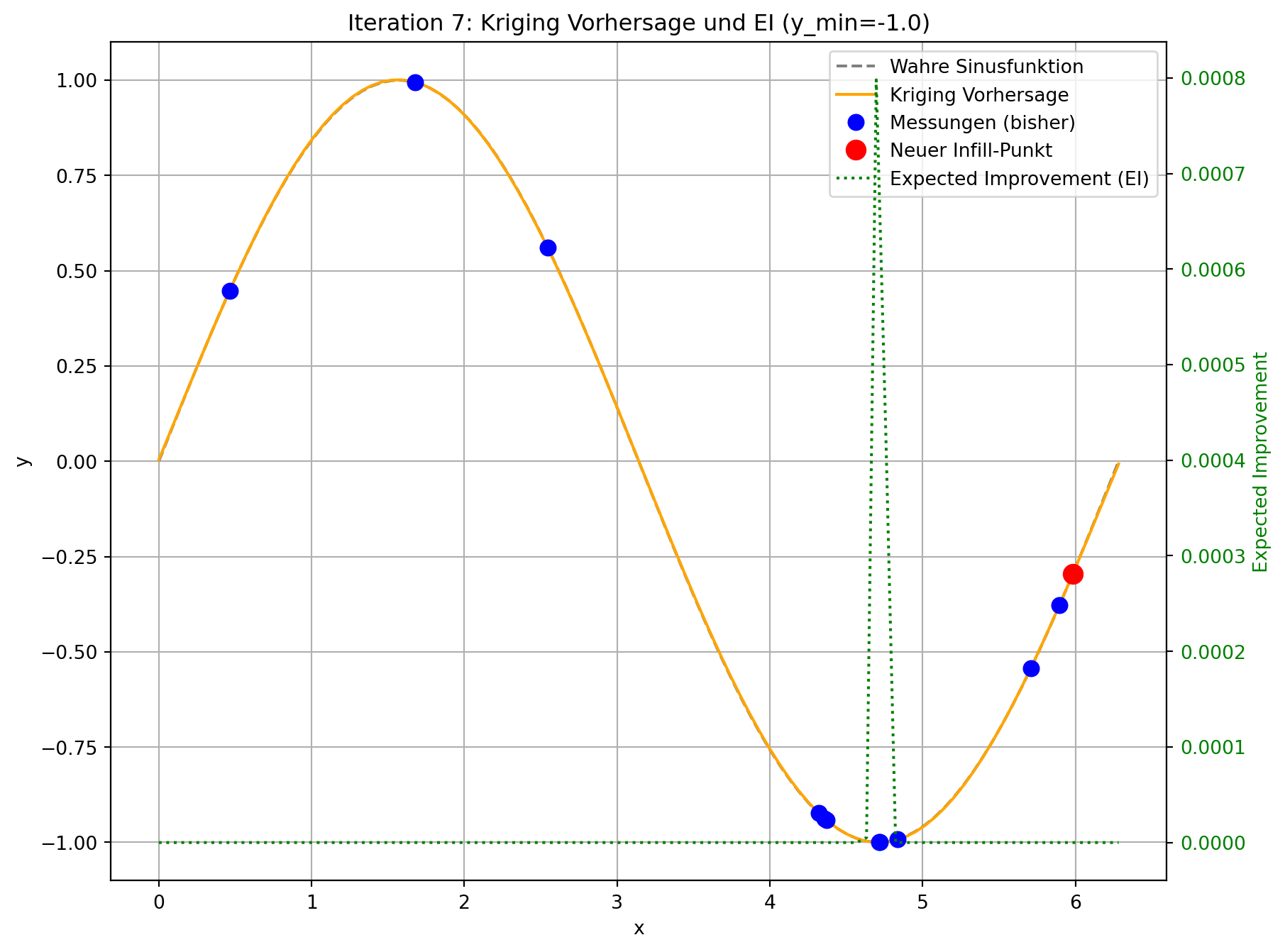
--- Iteration 8: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -1.0
Gewählter Infill-Punkt (standardisiert): [0.7809]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: -0.9812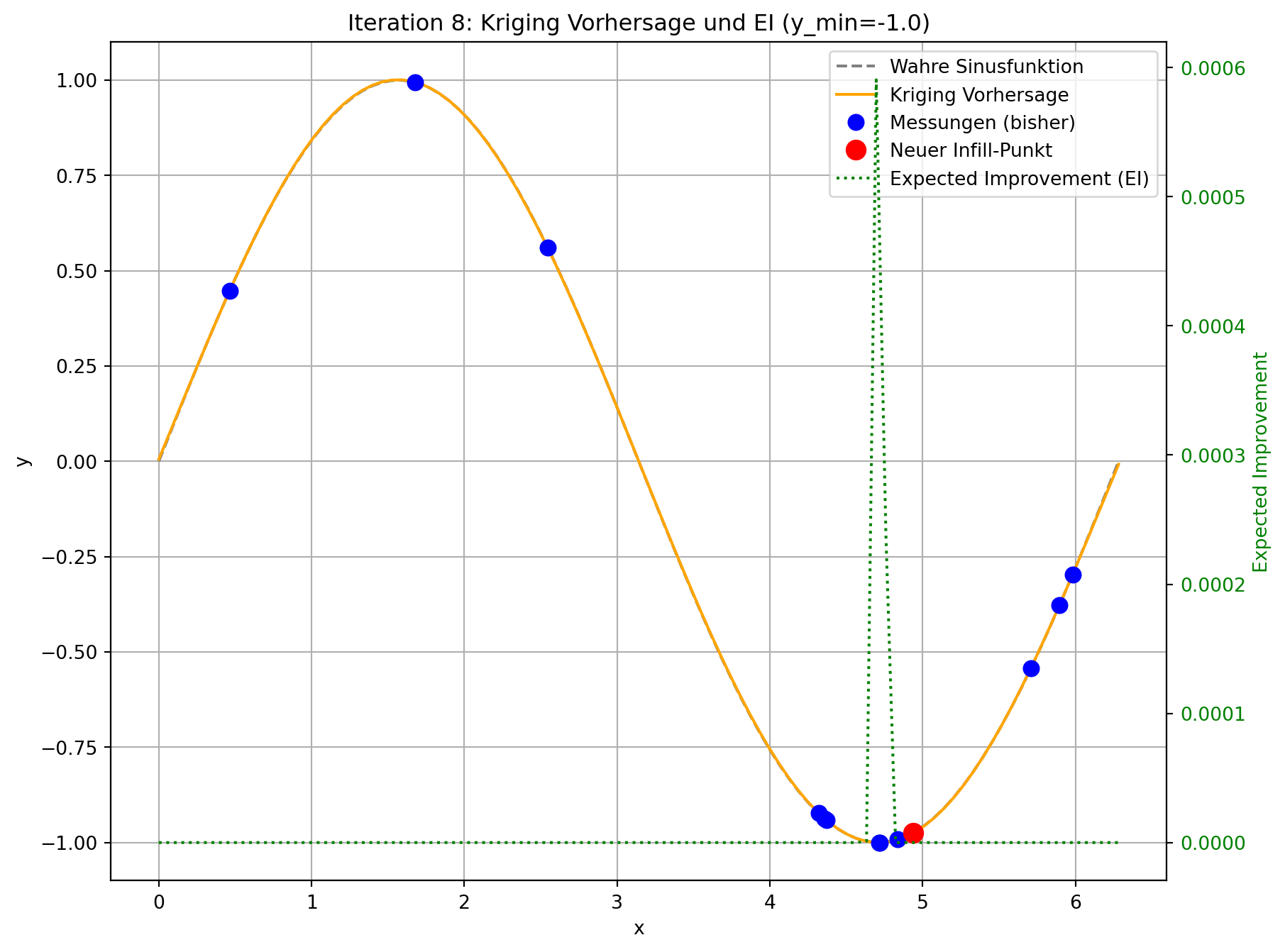
--- Iteration 9: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -1.0
Gewählter Infill-Punkt (standardisiert): [0.4665]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: 0.2089
--- Iteration 10: Suche Infill-Punkt mittels Expected Improvement ---
Bester bisheriger Wert (y_min): -1.0
Gewählter Infill-Punkt (standardisiert): [0.9265]
Geschätztes EI am Infill-Punkt: 0.0
Tatsächlicher Wert am Infill-Punkt: -0.4456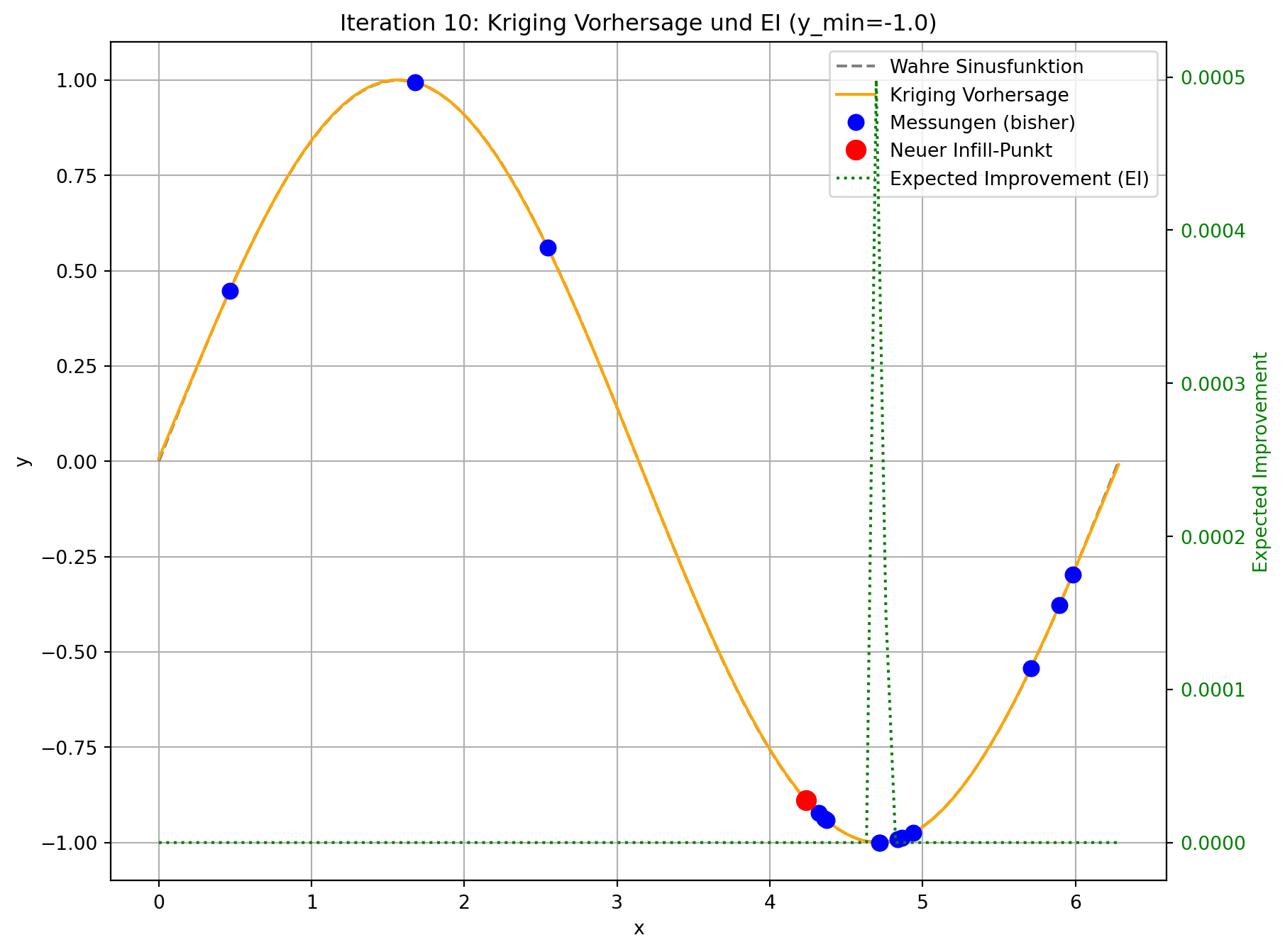
--- Optimierung abgeschlossen ---
Finaler bester Wert gefunden: -1.0
Gesamtzahl der Evaluierungen: 1570.2 Ergebnisse und Diskussion
Der angepasste Code demonstriert die Funktionsweise von Expected Improvement. In jeder Iteration wird nicht nur die Kriging-Vorhersage aktualisiert, sondern auch das Expected Improvement über den gesamten Designraum berechnet und visualisiert.
- Visuelle Darstellung: Sie werden sehen, dass die “Expected Improvement”-Kurve (grün gestrichelt) in Bereichen mit niedriger Vorhersage (gut für Exploitation) und/oder hoher Unsicherheit (gut für Exploration) hohe Werte aufweist. Der neue Infill-Punkt (roter Kreis) wird typischerweise an der Spitze eines solchen EI-Peaks platziert.
- Gleichgewicht: Im Gegensatz zur reinen Minimierung der Vorhersage, die dazu neigen könnte, in lokalen Minima stecken zu bleiben, fördert EI die Erkundung von Regionen, in denen das Modell unsicher ist, auch wenn die aktuelle Vorhersage dort nicht optimal ist. Dies ist besonders vorteilhaft bei multimodalen Funktionen oder wenn die initialen Stichproben den Designraum nicht vollständig abdecken.
- Konvergenz: Durch die kontinuierliche Hinzufügung von Punkten mit hohem Expected Improvement wird das Modell schrittweise genauer, und die Suche wird effizienter auf das globale Optimum hingeführt. Die EI-Werte nehmen typischerweise ab, wenn das Modell sicherer wird und das Optimum gefunden wird.
Dieses Modul zeigt, wie die Integration von Expected Improvement die Effizienz und Robustheit der sequenziellen Optimierung mit Kriging-Modellen erheblich verbessert, indem es eine intelligente Strategie zur Auswahl des nächsten Funktionsauswertungspunkts bereitstellt.