[54]{.chapter-number}  [Explainable AI with SpotPython and Pytorch]{.chapter-title}

doi:10.48550/arXiv.2307.10262

54 Explainable AI with SpotPython and Pytorch

Note, the divergence_threshold is set to 3,000, which is based on some pre-experiments with the user data set.

from spotpython.data.diabetes import Diabetes
from spotpython.hyperdict.light_hyper_dict import LightHyperDict
from spotpython.fun.hyperlight import HyperLight
from spotpython.utils.init import (fun_control_init, surrogate_control_init, design_control_init)
from spotpython.spot import Spot
from spotpython.utils.file import get_experiment_filename
from spotpython.hyperparameters.values import set_hyperparameter
from math import inf

PREFIX="602_12_1"

data_set = Diabetes()

fun_control = fun_control_init(
    save_experiment=True,
    PREFIX=PREFIX,
    fun_evals=inf,
    max_time=1,
    data_set = data_set,
    core_model_name="light.regression.NNLinearRegressor",
    hyperdict=LightHyperDict,
    divergence_threshold=3_000,
    _L_in=10,
    _L_out=1)

fun = HyperLight().fun


set_hyperparameter(fun_control, "optimizer", [ "Adadelta", "Adam", "Adamax"])
set_hyperparameter(fun_control, "l1", [3,7])
set_hyperparameter(fun_control, "epochs", [10,12])
set_hyperparameter(fun_control, "batch_size", [4,11])
set_hyperparameter(fun_control, "dropout_prob", [0.0, 0.025])
set_hyperparameter(fun_control, "patience", [2,9])

design_control = design_control_init(init_size=7)

S = Spot(fun=fun,fun_control=fun_control, design_control=design_control)

module_name: light
submodule_name: regression
model_name: NNLinearRegressor
Experiment saved to 602_12_1_exp.pkl

54.1 Running the Hyperparameter Tuning or Loading the Existing Model

S.run()

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 51.6 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.6 M

train_model result: {'val_loss': 24008.5703125, 'hp_metric': 24008.5703125}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  3.2 M │ train │ 816 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 3.2 M                                                                                            
Non-trainable params: 0                                                                                            
Total params: 3.2 M                                                                                                
Total estimated model params size (MB): 12                                                                         
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 816 M

train_model result: {'val_loss': 25638.1328125, 'hp_metric': 25638.1328125}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 4298.646484375, 'hp_metric': 4298.646484375}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃   In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  802 K │ train │ 1.6 B │ [1024, 10] │ [1024, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴────────────┴───────────┘

Trainable params: 802 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 802 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 1.6 B

train_model result: {'val_loss': 23521.087890625, 'hp_metric': 23521.087890625}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃   In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 12.7 M │ train │ 52.1 B │ [2048, 10] │ [2048, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴────────────┴───────────┘

Trainable params: 12.7 M                                                                                           
Non-trainable params: 0                                                                                            
Total params: 12.7 M                                                                                               
Total estimated model params size (MB): 50                                                                         
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 52.1 B

train_model result: {'val_loss': 234333.578125, 'hp_metric': 234333.578125}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 53.2 K │ train │ 52.5 M │ [512, 10] │  [512, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 53.2 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 53.2 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 52.5 M

train_model result: {'val_loss': 24054.228515625, 'hp_metric': 24054.228515625}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 24212.8515625, 'hp_metric': 24212.8515625}

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 25.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.6 M

train_model result: {'val_loss': 15141.951171875, 'hp_metric': 15141.951171875}
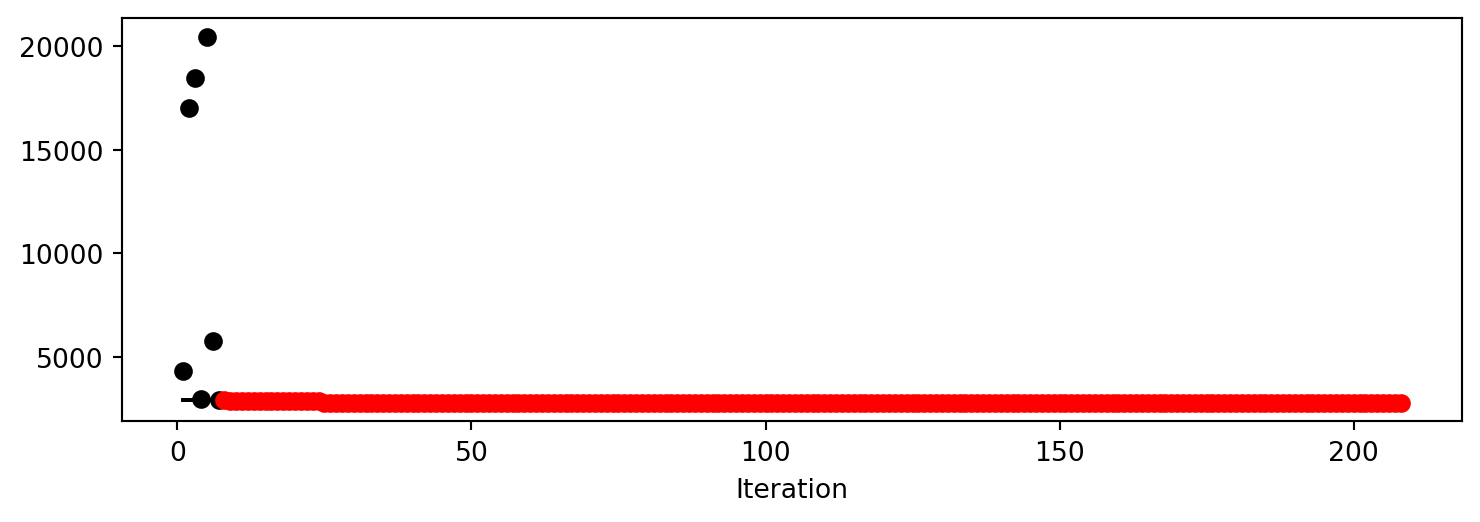
spotpython tuning: 4298.646484375 [----------] 1.25%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 25.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.6 M

train_model result: {'val_loss': 10541.05859375, 'hp_metric': 10541.05859375}
spotpython tuning: 4298.646484375 [----------] 2.89%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 6.5 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 6.5 M

train_model result: {'val_loss': 22962.96484375, 'hp_metric': 22962.96484375}
spotpython tuning: 4298.646484375 [----------] 4.47%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 12.7 M │ train │ 814 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 12.7 M                                                                                           
Non-trainable params: 0                                                                                            
Total params: 12.7 M                                                                                               
Total estimated model params size (MB): 50                                                                         
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 814 M

train_model result: {'val_loss': 77827.0234375, 'hp_metric': 77827.0234375}
spotpython tuning: 4298.646484375 [#---------] 6.53%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 23592.322265625, 'hp_metric': 23592.322265625}
spotpython tuning: 4298.646484375 [#---------] 7.10%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 3.3 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 3.3 M

train_model result: {'val_loss': 6308.0634765625, 'hp_metric': 6308.0634765625}
spotpython tuning: 4298.646484375 [#---------] 8.08%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 3.3 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 3.3 M

train_model result: {'val_loss': 24040.986328125, 'hp_metric': 24040.986328125}
spotpython tuning: 4298.646484375 [#---------] 9.34%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 3.3 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 3.3 M

train_model result: {'val_loss': 20776.10546875, 'hp_metric': 20776.10546875}
spotpython tuning: 4298.646484375 [#---------] 10.97%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 25.8 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.8 M

train_model result: {'val_loss': 23944.212890625, 'hp_metric': 23944.212890625}
spotpython tuning: 4298.646484375 [#---------] 11.92%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 103 M │ [256, 10] │  [256, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 103 M

train_model result: {'val_loss': 24245.560546875, 'hp_metric': 24245.560546875}
spotpython tuning: 4298.646484375 [#---------] 13.00%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  802 K │ train │ 102 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 802 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 802 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 102 M

train_model result: {'val_loss': 23191.6796875, 'hp_metric': 23191.6796875}
spotpython tuning: 4298.646484375 [#---------] 14.49%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 6.5 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 6.5 M

train_model result: {'val_loss': 22550.796875, 'hp_metric': 22550.796875}
spotpython tuning: 4298.646484375 [##--------] 16.05%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 25.8 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.8 M

train_model result: {'val_loss': 23998.98046875, 'hp_metric': 23998.98046875}
spotpython tuning: 4298.646484375 [##--------] 17.95%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 7605.974609375, 'hp_metric': 7605.974609375}
spotpython tuning: 4298.646484375 [##--------] 19.39%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 53.2 K │ train │ 6.6 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 53.2 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 53.2 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 6.6 M

train_model result: {'val_loss': 24050.08984375, 'hp_metric': 24050.08984375}
spotpython tuning: 4298.646484375 [##--------] 21.45%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 13179.0244140625, 'hp_metric': 13179.0244140625}
spotpython tuning: 4298.646484375 [##--------] 22.72%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 3.0394979793716095e+24, 'hp_metric': 3.0394979793716095e+24}
spotpython tuning: 4298.646484375 [##--------] 23.63%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 53.2 K │ train │ 52.5 M │ [512, 10] │  [512, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 53.2 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 53.2 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 52.5 M

train_model result: {'val_loss': 24071.0078125, 'hp_metric': 24071.0078125}
spotpython tuning: 4298.646484375 [###-------] 26.13%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 22922.708984375, 'hp_metric': 22922.708984375}
spotpython tuning: 4298.646484375 [###-------] 26.88%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 21665.01953125, 'hp_metric': 21665.01953125}
spotpython tuning: 4298.646484375 [###-------] 31.33%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 24376.826171875, 'hp_metric': 24376.826171875}
spotpython tuning: 4298.646484375 [###-------] 34.39%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 52.5 M │ [512, 10] │  [512, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 52.5 M

train_model result: {'val_loss': 23619.865234375, 'hp_metric': 23619.865234375}
spotpython tuning: 4298.646484375 [####------] 36.29%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  802 K │ train │ 819 M │ [512, 10] │  [512, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 802 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 802 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 819 M

train_model result: {'val_loss': 23855.919921875, 'hp_metric': 23855.919921875}
spotpython tuning: 4298.646484375 [####------] 39.63%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  802 K │ train │ 204 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 802 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 802 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 204 M

train_model result: {'val_loss': 18489.638671875, 'hp_metric': 18489.638671875}
spotpython tuning: 4298.646484375 [####------] 42.13%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 53.2 K │ train │ 6.6 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 53.2 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 53.2 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 6.6 M

train_model result: {'val_loss': 24000.38671875, 'hp_metric': 24000.38671875}
spotpython tuning: 4298.646484375 [####------] 44.69%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 23436.99609375, 'hp_metric': 23436.99609375}
spotpython tuning: 4298.646484375 [#####-----] 49.02%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 103 M │ [256, 10] │  [256, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 103 M

train_model result: {'val_loss': 24025.77734375, 'hp_metric': 24025.77734375}
spotpython tuning: 4298.646484375 [#####-----] 50.85%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 51.6 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.6 M

train_model result: {'val_loss': 24050.146484375, 'hp_metric': 24050.146484375}
spotpython tuning: 4298.646484375 [#####-----] 53.32%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 25.8 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.8 M

train_model result: {'val_loss': 23898.478515625, 'hp_metric': 23898.478515625}
spotpython tuning: 4298.646484375 [######----] 55.86%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 51.2 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.2 M

train_model result: {'val_loss': 20080.798828125, 'hp_metric': 20080.798828125}
spotpython tuning: 4298.646484375 [######----] 57.54%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 53.2 K │ train │ 13.1 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 53.2 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 53.2 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 13.1 M

train_model result: {'val_loss': 24015.955078125, 'hp_metric': 24015.955078125}
spotpython tuning: 4298.646484375 [######----] 60.36%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 51.6 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 51.6 M

train_model result: {'val_loss': 24050.486328125, 'hp_metric': 24050.486328125}
spotpython tuning: 4298.646484375 [######----] 64.32%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  3.2 M │ train │ 102 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 3.2 M                                                                                            
Non-trainable params: 0                                                                                            
Total params: 3.2 M                                                                                                
Total estimated model params size (MB): 12                                                                         
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 102 M

train_model result: {'val_loss': 17813.669921875, 'hp_metric': 17813.669921875}
spotpython tuning: 4298.646484375 [#######---] 67.94%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 3.3 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 3.3 M

train_model result: {'val_loss': 22139.86328125, 'hp_metric': 22139.86328125}
spotpython tuning: 4298.646484375 [#######---] 71.39%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 6.5 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 6.5 M

train_model result: {'val_loss': 24036.263671875, 'hp_metric': 24036.263671875}
spotpython tuning: 4298.646484375 [########--] 75.07%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 1.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 1.6 M

train_model result: {'val_loss': 21281.712890625, 'hp_metric': 21281.712890625}
spotpython tuning: 4298.646484375 [########--] 78.08%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 1.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 1.6 M

train_model result: {'val_loss': 5334.50048828125, 'hp_metric': 5334.50048828125}
spotpython tuning: 4298.646484375 [########--] 81.38%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 6.5 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 6.5 M

train_model result: {'val_loss': 24019.35546875, 'hp_metric': 24019.35546875}
spotpython tuning: 4298.646484375 [#########-] 85.05%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 51.9 K │ train │ 1.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴──────────┴───────────┘

Trainable params: 51.9 K                                                                                           
Non-trainable params: 0                                                                                            
Total params: 51.9 K                                                                                               
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 1.6 M

train_model result: {'val_loss': 5027.46240234375, 'hp_metric': 5027.46240234375}
spotpython tuning: 4298.646484375 [#########-] 88.36%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  3.2 M │ train │ 816 M │ [128, 10] │  [128, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 3.2 M                                                                                            
Non-trainable params: 0                                                                                            
Total params: 3.2 M                                                                                                
Total estimated model params size (MB): 12                                                                         
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 816 M

train_model result: {'val_loss': 724579.1875, 'hp_metric': 724579.1875}
spotpython tuning: 4298.646484375 [#########-] 89.59%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  807 K │ train │ 25.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 807 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 807 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.6 M

train_model result: {'val_loss': 24025.4453125, 'hp_metric': 24025.4453125}
spotpython tuning: 4298.646484375 [#########-] 92.27%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 103 M │ [256, 10] │  [256, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 103 M

train_model result: {'val_loss': 23999.83203125, 'hp_metric': 23999.83203125}
spotpython tuning: 4298.646484375 [#########-] 93.96%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  802 K │ train │ 25.6 M │ [16, 10] │   [16, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 802 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 802 K                                                                                                
Total estimated model params size (MB): 3                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.6 M

train_model result: {'val_loss': 19088.296875, 'hp_metric': 19088.296875}
spotpython tuning: 4298.646484375 [##########] 95.92%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  205 K │ train │ 25.8 M │ [64, 10] │   [64, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 205 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 205 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 24                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 25.8 M

train_model result: {'val_loss': 24011.466796875, 'hp_metric': 24011.466796875}
spotpython tuning: 4298.646484375 [##########] 97.75%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃ FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  3.2 M │ train │ 3.3 B │ [512, 10] │  [512, 1] │
└───┴────────┴────────────┴────────┴───────┴───────┴───────────┴───────────┘

Trainable params: 3.2 M                                                                                            
Non-trainable params: 0                                                                                            
Total params: 3.2 M                                                                                                
Total estimated model params size (MB): 12                                                                         
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 3.3 B

train_model result: {'val_loss': 13796.8359375, 'hp_metric': 13796.8359375}
spotpython tuning: 4298.646484375 [##########] 98.57%. Success rate: 0.00%

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃  In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │ 12.7 M │ train │ 13.0 B │ [512, 10] │  [512, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴───────────┴───────────┘

Trainable params: 12.7 M                                                                                           
Non-trainable params: 0                                                                                            
Total params: 12.7 M                                                                                               
Total estimated model params size (MB): 50                                                                         
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 13.0 B

train_model result: {'val_loss': 76184.4921875, 'hp_metric': 76184.4921875}
spotpython tuning: 4298.646484375 [##########] 100.00%. Success rate: 0.00% Done...

Experiment saved to 602_12_1_res.pkl

<spotpython.spot.spot.Spot at 0x1533ec830>

54.2 Results from the Hyperparameter Tuning Experiment

After the hyperparameter tuning is finished, the following information is available:
- the S object and the associated
- fun_control dictionary

S.print_results(print_screen=True)

min y: 4298.646484375
l1: 4.0
epochs: 12.0
batch_size: 5.0
act_fn: 2.0
optimizer: 1.0
dropout_prob: 0.0035182324401420283
lr_mult: 5.090825861997777
patience: 2.0
batch_norm: 0.0
initialization: 1.0

[['l1', np.float64(4.0)],
 ['epochs', np.float64(12.0)],
 ['batch_size', np.float64(5.0)],
 ['act_fn', np.float64(2.0)],
 ['optimizer', np.float64(1.0)],
 ['dropout_prob', np.float64(0.0035182324401420283)],
 ['lr_mult', np.float64(5.090825861997777)],
 ['patience', np.float64(2.0)],
 ['batch_norm', np.float64(0.0)],
 ['initialization', np.float64(1.0)]]

S.plot_progress()

54.2.1 Getting the Best Model, i.e, the Tuned Architecture

The method get_tuned_architecture [DOC] returns the best model architecture found during the hyperparameter tuning.
It returns the transformed values, i.e., batch_size = 2^x if the hyperparameter batch_size was transformed with the transform_power_2_int function.

from spotpython.hyperparameters.values import get_tuned_architecture
import pprint
config = get_tuned_architecture(S)
pprint.pprint(config)

{'act_fn': ReLU(),
 'batch_norm': False,
 'batch_size': 32,
 'dropout_prob': 0.0035182324401420283,
 'epochs': 4096,
 'initialization': 'kaiming_uniform',
 'l1': 16,
 'lr_mult': 5.090825861997777,
 'optimizer': 'Adam',
 'patience': 4}

Note: get_tuned_architecture has the option force_minX which does not have any effect in this case.

from spotpython.hyperparameters.values import get_tuned_architecture
config = get_tuned_architecture(S, force_minX=True)
pprint.pprint(config)

{'act_fn': ReLU(),
 'batch_norm': False,
 'batch_size': 32,
 'dropout_prob': 0.0035182324401420283,
 'epochs': 4096,
 'initialization': 'kaiming_uniform',
 'l1': 16,
 'lr_mult': 5.090825861997777,
 'optimizer': 'Adam',
 'patience': 4}

54.3 Training the Tuned Architecture on the Test Data

Since we are interested in the explainability of the model, we will train the tuned architecture on the test data.
spotpythons’s test_model function [DOC] is used to train the model on the test data.
Note: Until now, we do not use any information about the NN’s weights and biases. Only the architecture, which is available as the config, is used.
spotpython used the TensorBoard logger to save the training process in the ./runs directory. Therefore, we have to enable the TensorBoard logger in the fun_control dictionary. To get a clean start, we remove an existing runs folder.

from spotpython.light.testmodel import test_model
from spotpython.light.loadmodel import load_light_from_checkpoint
fun_control.update({"tensorboard_log": True})
test_model(config, fun_control)

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

┏━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━┓
┃        Test metric        ┃       DataLoader 0        ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━┩
│         hp_metric         │     3018.216064453125     │
│         val_loss          │     3018.216064453125     │
└───────────────────────────┴───────────────────────────┘

test_model result: {'val_loss': 3018.216064453125, 'hp_metric': 3018.216064453125}

(3018.216064453125, 3018.216064453125)

model = load_light_from_checkpoint(config, fun_control)

config: {'l1': 16, 'epochs': 4096, 'batch_size': 32, 'act_fn': ReLU(), 'optimizer': 'Adam', 'dropout_prob': 0.0035182324401420283, 'lr_mult': 5.090825861997777, 'patience': 4, 'batch_norm': False, 'initialization': 'kaiming_uniform'}
Loading model with 16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TEST from runs/saved_models/16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TEST/last.ckpt
Model: NNLinearRegressor(
  (layers): Sequential(
    (0): Linear(in_features=10, out_features=320, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.0035182324401420283, inplace=False)
    (3): Linear(in_features=320, out_features=160, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.0035182324401420283, inplace=False)
    (6): Linear(in_features=160, out_features=320, bias=True)
    (7): ReLU()
    (8): Dropout(p=0.0035182324401420283, inplace=False)
    (9): Linear(in_features=320, out_features=160, bias=True)
    (10): ReLU()
    (11): Dropout(p=0.0035182324401420283, inplace=False)
    (12): Linear(in_features=160, out_features=160, bias=True)
    (13): ReLU()
    (14): Dropout(p=0.0035182324401420283, inplace=False)
    (15): Linear(in_features=160, out_features=80, bias=True)
    (16): ReLU()
    (17): Dropout(p=0.0035182324401420283, inplace=False)
    (18): Linear(in_features=80, out_features=80, bias=True)
    (19): ReLU()
    (20): Dropout(p=0.0035182324401420283, inplace=False)
    (21): Linear(in_features=80, out_features=1, bias=True)
  )
)

54.3.0.1 Details of the Training Process on the Test Data

The test_model method initializes the model with the tuned architecture as follows:

model = fun_control["core_model"](**config, _L_in=_L_in, _L_out=_L_out, _torchmetric=_torchmetric)

Then, the Lightning Trainer is initialized with the fun_control dictionary and the model as follows:

    trainer = L.Trainer(
    default_root_dir=os.path.join(fun_control["CHECKPOINT_PATH"], config_id),
    max_epochs=model.hparams.epochs,
    accelerator=fun_control["accelerator"],
    devices=fun_control["devices"],
    logger=TensorBoardLogger(
        save_dir=fun_control["TENSORBOARD_PATH"],
        version=config_id,
        default_hp_metric=True,
        log_graph=fun_control["log_graph"],
    ),
    callbacks=[
        EarlyStopping(monitor="val_loss", patience=config["patience"], mode="min", strict=False, verbose=False),
        ModelCheckpoint(
            dirpath=os.path.join(fun_control["CHECKPOINT_PATH"], config_id), save_last=True
        ), 
    ],
    enable_progress_bar=enable_progress_bar,
)
trainer.fit(model=model, datamodule=dm)    
test_result = trainer.test(datamodule=dm, ckpt_path="last")

As shown in the code above, the last checkpoint ist saved.
spotpython’s method load_light_from_checkpoint is used to load the last checkpoint and to get the model’s weights and biases. It requires the fun_control dictionary and the config_id as input to find the correct checkpoint.
Now, the model is trained and the weights and biases are available.

54.4 Visualizing the Neural Network Architecture

# get the device
from spotpython.utils.device import getDevice
device = getDevice()

from spotpython.plot.xai import viz_net
viz_net(model, device=device)

54.5 XAI Methods

spotpython provides methods to explain the model’s predictions. The following neural network elements can be analyzed:

54.5.1 Weights

Weights are the parameters of the neural network that are learned from the data during training. They connect neurons between layers and determine the strength and direction of the signal sent from one neuron to another. The network adjusts the weights during training to minimize the error between the predicted output and the actual output.
Interpretation of the weights: A high weight value indicates a strong influence of the input neuron on the output. Positive weights suggest a positive correlation, whereas negative weights suggest an inverse relationship between neurons.

54.5.2 Activations

Activations are the outputs produced by neurons after applying an activation function to the weighted sum of inputs. The activation function (e.g., ReLU, sigmoid, tanh) adds non-linearity to the model, allowing it to learn more complex relationships.
Interpretation of the activations: The value of activations indicates the intensity of the signal passed to the next layer. Certain activation patterns can highlight which features or parts of the data the network is focusing on.

54.5.3 Gradients

Gradients are the partial derivatives of the loss function with respect to different parameters (weights) of the network. During backpropagation, gradients are used to update the weights in the direction that reduces the loss by methods like gradient descent.
Interpretation of the gradients: The magnitude of the gradient indicates how much a parameter should change to reduce the error. A large gradient implies a steeper slope and a bigger update, while a small gradient suggests that the parameter is near an optimal point. If gradients are too small (vanishing gradient problem), the network may learn slowly or stop learning. If they are too large (exploding gradient problem), the updates may be unstable.
sptpython provides the method get_gradients to get the gradients of the model.

from spotpython.plot.xai import (get_activations, get_gradients, get_weights, visualize_weights, visualize_gradients, visualize_mean_activations, visualize_gradient_distributions, visualize_weights_distributions, visualize_activations_distributions)
batch_size = config["batch_size"]

54.5.4 Getting the Weights

from spotpython.plot.xai import sort_layers
weights, _ = get_weights(model)
# sort_layers(weights)

visualize_weights(model, absolute=True, cmap="GreenYellowRed", figsize=(6, 6))

3200 values in Layer Layer 0. Geometry: (320, 10)

51200 values in Layer Layer 3. Geometry: (160, 320)

51200 values in Layer Layer 6. Geometry: (320, 160)

51200 values in Layer Layer 9. Geometry: (160, 320)

25600 values in Layer Layer 12. Geometry: (160, 160)

12800 values in Layer Layer 15. Geometry: (80, 160)

6400 values in Layer Layer 18. Geometry: (80, 80)

80 values in Layer Layer 21. Geometry: (1, 80)

visualize_weights_distributions(model, color=f"C{0}", columns=4)

n:8

54.5.5 Getting the Activations

from spotpython.plot.xai import get_activations
activations, mean_activations, layer_sizes = get_activations(net=model, fun_control=fun_control, batch_size=batch_size, device=device)

train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting train & val data.
train samples: 160, val samples: 106 generated for train & val data.
LightDataModule.train_dataloader(). data_train size: 160

visualize_mean_activations(mean_activations, layer_sizes=layer_sizes, absolute=True, cmap="GreenYellowRed", figsize=(6, 6))

320 values in Layer 0. Geometry: (1, 320)

160 values in Layer 3. Geometry: (1, 160)

320 values in Layer 6. Geometry: (1, 320)

160 values in Layer 9. Geometry: (1, 160)

160 values in Layer 12. Geometry: (1, 160)

80 values in Layer 15. Geometry: (1, 80)

80 values in Layer 18. Geometry: (1, 80)

visualize_activations_distributions(activations=activations,
                                    net=model, color="C0", columns=4)

54.5.6 Getting the Gradients

gradients, _ = get_gradients(net=model, fun_control=fun_control, batch_size=batch_size, device=device)

train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting train & val data.
train samples: 160, val samples: 106 generated for train & val data.
LightDataModule.train_dataloader(). data_train size: 160

visualize_gradients(model, fun_control, batch_size, absolute=True, cmap="GreenYellowRed", figsize=(6, 6), device=device)

train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting train & val data.
train samples: 160, val samples: 106 generated for train & val data.
LightDataModule.train_dataloader(). data_train size: 160
3200 values in Layer layers.0.weight. Geometry: (320, 10)

51200 values in Layer layers.3.weight. Geometry: (160, 320)

51200 values in Layer layers.6.weight. Geometry: (320, 160)

51200 values in Layer layers.9.weight. Geometry: (160, 320)

25600 values in Layer layers.12.weight. Geometry: (160, 160)

12800 values in Layer layers.15.weight. Geometry: (80, 160)

6400 values in Layer layers.18.weight. Geometry: (80, 80)

80 values in Layer layers.21.weight. Geometry: (1, 80)

visualize_gradient_distributions(model, fun_control, batch_size=batch_size, color=f"C{0}", device=device, columns=3)

train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting train & val data.
train samples: 160, val samples: 106 generated for train & val data.
LightDataModule.train_dataloader(). data_train size: 160
n:8

54.6 Feature Attributions

54.6.1 Integrated Gradients

from spotpython.plot.xai import get_attributions, plot_attributions
df_att = get_attributions(S, fun_control, attr_method="IntegratedGradients", n_rel=10)
plot_attributions(df_att, attr_method="IntegratedGradients")

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 4339.142578125, 'hp_metric': 4339.142578125}
config: {'l1': 16, 'epochs': 4096, 'batch_size': 32, 'act_fn': ReLU(), 'optimizer': 'Adam', 'dropout_prob': 0.0035182324401420283, 'lr_mult': 5.090825861997777, 'patience': 4, 'batch_norm': False, 'initialization': 'kaiming_uniform'}
Loading model with 16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN from runs/saved_models/16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN/last.ckpt
Model: NNLinearRegressor(
  (layers): Sequential(
    (0): Linear(in_features=10, out_features=320, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.0035182324401420283, inplace=False)
    (3): Linear(in_features=320, out_features=160, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.0035182324401420283, inplace=False)
    (6): Linear(in_features=160, out_features=320, bias=True)
    (7): ReLU()
    (8): Dropout(p=0.0035182324401420283, inplace=False)
    (9): Linear(in_features=320, out_features=160, bias=True)
    (10): ReLU()
    (11): Dropout(p=0.0035182324401420283, inplace=False)
    (12): Linear(in_features=160, out_features=160, bias=True)
    (13): ReLU()
    (14): Dropout(p=0.0035182324401420283, inplace=False)
    (15): Linear(in_features=160, out_features=80, bias=True)
    (16): ReLU()
    (17): Dropout(p=0.0035182324401420283, inplace=False)
    (18): Linear(in_features=80, out_features=80, bias=True)
    (19): ReLU()
    (20): Dropout(p=0.0035182324401420283, inplace=False)
    (21): Linear(in_features=80, out_features=1, bias=True)
  )
)
train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting test data.
test samples: 177 generated for test data.
LightDataModule.test_dataloader(). Test set size: 177

54.6.2 Deep Lift

df_lift = get_attributions(S, fun_control, attr_method="DeepLift",n_rel=10)
print(df_lift)
plot_attributions(df_lift,  attr_method="DeepLift")

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 4411.060546875, 'hp_metric': 4411.060546875}
config: {'l1': 16, 'epochs': 4096, 'batch_size': 32, 'act_fn': ReLU(), 'optimizer': 'Adam', 'dropout_prob': 0.0035182324401420283, 'lr_mult': 5.090825861997777, 'patience': 4, 'batch_norm': False, 'initialization': 'kaiming_uniform'}
Loading model with 16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN from runs/saved_models/16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN/last.ckpt
Model: NNLinearRegressor(
  (layers): Sequential(
    (0): Linear(in_features=10, out_features=320, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.0035182324401420283, inplace=False)
    (3): Linear(in_features=320, out_features=160, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.0035182324401420283, inplace=False)
    (6): Linear(in_features=160, out_features=320, bias=True)
    (7): ReLU()
    (8): Dropout(p=0.0035182324401420283, inplace=False)
    (9): Linear(in_features=320, out_features=160, bias=True)
    (10): ReLU()
    (11): Dropout(p=0.0035182324401420283, inplace=False)
    (12): Linear(in_features=160, out_features=160, bias=True)
    (13): ReLU()
    (14): Dropout(p=0.0035182324401420283, inplace=False)
    (15): Linear(in_features=160, out_features=80, bias=True)
    (16): ReLU()
    (17): Dropout(p=0.0035182324401420283, inplace=False)
    (18): Linear(in_features=80, out_features=80, bias=True)
    (19): ReLU()
    (20): Dropout(p=0.0035182324401420283, inplace=False)
    (21): Linear(in_features=80, out_features=1, bias=True)
  )
)
train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting test data.
test samples: 177 generated for test data.
LightDataModule.test_dataloader(). Test set size: 177
   Feature Index Feature  DeepLiftAttribution
0              1     sex          1026.236694
1              9  s6_glu          1026.086426
2              0     age          1012.324463
3              6  s3_hdl           988.167114
4              3      bp           953.655762
5              4   s1_tc           916.110718
6              8  s5_ltg           913.878418
7              7  s4_tch           854.368530
8              5  s2_ldl           848.338867
9              2     bmi           782.169434

54.6.3 Feature Ablation

df_fl = get_attributions(S, fun_control, attr_method="FeatureAblation",n_rel=10)

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 7301.94921875, 'hp_metric': 7301.94921875}
config: {'l1': 16, 'epochs': 4096, 'batch_size': 32, 'act_fn': ReLU(), 'optimizer': 'Adam', 'dropout_prob': 0.0035182324401420283, 'lr_mult': 5.090825861997777, 'patience': 4, 'batch_norm': False, 'initialization': 'kaiming_uniform'}
Loading model with 16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN from runs/saved_models/16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN/last.ckpt
Model: NNLinearRegressor(
  (layers): Sequential(
    (0): Linear(in_features=10, out_features=320, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.0035182324401420283, inplace=False)
    (3): Linear(in_features=320, out_features=160, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.0035182324401420283, inplace=False)
    (6): Linear(in_features=160, out_features=320, bias=True)
    (7): ReLU()
    (8): Dropout(p=0.0035182324401420283, inplace=False)
    (9): Linear(in_features=320, out_features=160, bias=True)
    (10): ReLU()
    (11): Dropout(p=0.0035182324401420283, inplace=False)
    (12): Linear(in_features=160, out_features=160, bias=True)
    (13): ReLU()
    (14): Dropout(p=0.0035182324401420283, inplace=False)
    (15): Linear(in_features=160, out_features=80, bias=True)
    (16): ReLU()
    (17): Dropout(p=0.0035182324401420283, inplace=False)
    (18): Linear(in_features=80, out_features=80, bias=True)
    (19): ReLU()
    (20): Dropout(p=0.0035182324401420283, inplace=False)
    (21): Linear(in_features=80, out_features=1, bias=True)
  )
)
train_size: 0.36, val_size: 0.24, test_sie: 0.4 for splitting test data.
test samples: 177 generated for test data.
LightDataModule.test_dataloader(). Test set size: 177

print(df_fl)
plot_attributions(df_fl, attr_method="FeatureAblation")

   Feature Index Feature  FeatureAblationAttribution
0              9  s6_glu                  577.062134
1              0     age                  556.625305
2              6  s3_hdl                  554.604370
3              3      bp                  528.497559
4              8  s5_ltg                  527.454163
5              4   s1_tc                  523.947937
6              1     sex                  519.197693
7              5  s2_ldl                  463.207764
8              7  s4_tch                  440.091187
9              2     bmi                  371.574615

54.7 Conductance

from spotpython.plot.xai import plot_conductance_last_layer, get_weights_conductance_last_layer
weights_last, layer_conductance_last = get_weights_conductance_last_layer(S, fun_control)
plot_conductance_last_layer(weights_last, layer_conductance_last, figsize=(6, 6))

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 10892.2080078125, 'hp_metric': 10892.2080078125}
config: {'l1': 16, 'epochs': 4096, 'batch_size': 32, 'act_fn': ReLU(), 'optimizer': 'Adam', 'dropout_prob': 0.0035182324401420283, 'lr_mult': 5.090825861997777, 'patience': 4, 'batch_norm': False, 'initialization': 'kaiming_uniform'}
Loading model with 16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN from runs/saved_models/16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN/last.ckpt

Model: NNLinearRegressor(
  (layers): Sequential(
    (0): Linear(in_features=10, out_features=320, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.0035182324401420283, inplace=False)
    (3): Linear(in_features=320, out_features=160, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.0035182324401420283, inplace=False)
    (6): Linear(in_features=160, out_features=320, bias=True)
    (7): ReLU()
    (8): Dropout(p=0.0035182324401420283, inplace=False)
    (9): Linear(in_features=320, out_features=160, bias=True)
    (10): ReLU()
    (11): Dropout(p=0.0035182324401420283, inplace=False)
    (12): Linear(in_features=160, out_features=160, bias=True)
    (13): ReLU()
    (14): Dropout(p=0.0035182324401420283, inplace=False)
    (15): Linear(in_features=160, out_features=80, bias=True)
    (16): ReLU()
    (17): Dropout(p=0.0035182324401420283, inplace=False)
    (18): Linear(in_features=80, out_features=80, bias=True)
    (19): ReLU()
    (20): Dropout(p=0.0035182324401420283, inplace=False)
    (21): Linear(in_features=80, out_features=1, bias=True)
  )
)

┏━━━┳━━━━━━━━┳━━━━━━━━━━━━┳━━━━━━━━┳━━━━━━━┳━━━━━━━━┳━━━━━━━━━━┳━━━━━━━━━━━┓
┃   ┃ Name   ┃ Type       ┃ Params ┃ Mode  ┃  FLOPs ┃ In sizes ┃ Out sizes ┃
┡━━━╇━━━━━━━━╇━━━━━━━━━━━━╇━━━━━━━━╇━━━━━━━╇━━━━━━━━╇━━━━━━━━━━╇━━━━━━━━━━━┩
│ 0 │ layers │ Sequential │  202 K │ train │ 12.9 M │ [32, 10] │   [32, 1] │
└───┴────────┴────────────┴────────┴───────┴────────┴──────────┴───────────┘

Trainable params: 202 K                                                                                            
Non-trainable params: 0                                                                                            
Total params: 202 K                                                                                                
Total estimated model params size (MB): 0                                                                          
Modules in train mode: 17                                                                                          
Modules in eval mode: 0                                                                                            
Total FLOPs: 12.9 M

train_model result: {'val_loss': 11865.244140625, 'hp_metric': 11865.244140625}
config: {'l1': 16, 'epochs': 4096, 'batch_size': 32, 'act_fn': ReLU(), 'optimizer': 'Adam', 'dropout_prob': 0.0035182324401420283, 'lr_mult': 5.090825861997777, 'patience': 4, 'batch_norm': False, 'initialization': 'kaiming_uniform'}
Loading model with 16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN from runs/saved_models/16_4096_32_ReLU_Adam_0.0035_5.0908_4_False_kaiming_uniform_TRAIN/last.ckpt
Model: NNLinearRegressor(
  (layers): Sequential(
    (0): Linear(in_features=10, out_features=320, bias=True)
    (1): ReLU()
    (2): Dropout(p=0.0035182324401420283, inplace=False)
    (3): Linear(in_features=320, out_features=160, bias=True)
    (4): ReLU()
    (5): Dropout(p=0.0035182324401420283, inplace=False)
    (6): Linear(in_features=160, out_features=320, bias=True)
    (7): ReLU()
    (8): Dropout(p=0.0035182324401420283, inplace=False)
    (9): Linear(in_features=320, out_features=160, bias=True)
    (10): ReLU()
    (11): Dropout(p=0.0035182324401420283, inplace=False)
    (12): Linear(in_features=160, out_features=160, bias=True)
    (13): ReLU()
    (14): Dropout(p=0.0035182324401420283, inplace=False)
    (15): Linear(in_features=160, out_features=80, bias=True)
    (16): ReLU()
    (17): Dropout(p=0.0035182324401420283, inplace=False)
    (18): Linear(in_features=80, out_features=80, bias=True)
    (19): ReLU()
    (20): Dropout(p=0.0035182324401420283, inplace=False)
    (21): Linear(in_features=80, out_features=1, bias=True)
  )
)
Conductance analysis for layer:  Linear(in_features=80, out_features=1, bias=True)