14  Isotropic and Anisotropic Kriging

This chapter illustrates the difference between isotropic and anisotropic Kriging models. The difference is illustrated with the help of the spotpython package. Isotropic Kriging models use the same theta value for every dimension. Anisotropic Kriging models use different theta values for each dimension.

14.1 Example: Isotropic Spot Surrogate and the 2-dim Sphere Function

import numpy as np
from math import inf
from spotpython.fun.objectivefunctions import Analytical
from spotpython.spot import Spot
from spotpython.utils.init import fun_control_init, surrogate_control_init
PREFIX="003"

14.1.1 The Objective Function: 2-dim Sphere

The spotpython package provides several classes of objective functions. We will use an analytical objective function, i.e., a function that can be described by a (closed) formula:

\[ f(x, y) = x^2 + y^2 \] The size of the lower bound vector determines the problem dimension. Here we will use np.array([-1, -1]), i.e., a two-dimensional function.

fun = Analytical().fun_sphere
fun_control = fun_control_init(PREFIX=PREFIX,
                               lower = np.array([-1, -1]),
                               upper = np.array([1, 1]))

The default Spot surrogate model is an anisotropic Kriging model. We will explicitly set the isotropic parameter to a value of False, so that the same theta value is used for both dimensions. This is done to illustrate the difference between isotropic and anisotropic Kriging models.

surrogate_control=surrogate_control_init(isotropic=True)
spot_2 = Spot(fun=fun,
                   fun_control=fun_control,
                   surrogate_control=surrogate_control)

spot_2.run()
Isotropic model: n_theta set to 1
Isotropic model: n_theta set to 1
spotpython tuning: 0.0025690787279226534 [#######---] 73.33% 
Isotropic model: n_theta set to 1
spotpython tuning: 0.0025690787279226534 [########--] 80.00% 
Isotropic model: n_theta set to 1
spotpython tuning: 0.0025690787279226534 [#########-] 86.67% 
Isotropic model: n_theta set to 1
spotpython tuning: 0.0025690787279226534 [#########-] 93.33% 
Isotropic model: n_theta set to 1
spotpython tuning: 0.0025690787279226534 [##########] 100.00% Done...

Experiment saved to 003_res.pkl
<spotpython.spot.spot.Spot at 0x104428050>

14.1.2 Results

spot_2.print_results()
min y: 0.0025690787279226534
x0: 0.031663980166141595
x1: 0.03957866960827315
[['x0', np.float64(0.031663980166141595)],
 ['x1', np.float64(0.03957866960827315)]]
spot_2.plot_progress(log_y=True)

14.2 Example With Anisotropic Kriging

As described in Section 14.1, the default parameter setting of spotpython’s Kriging surrogate uses different theta value for every dimension. This is referred to as “using an anisotropic kernel”. To enable isotropic models in spotpython, the command surrogate_control=surrogate_control_init(isotropic=True) can be used. In this case, the same theta value is used for every dimension.

spot_2_anisotropic = Spot(fun=fun,
                    fun_control=fun_control)
spot_2_anisotropic.run()
Anisotropic model: n_theta set to 2
Anisotropic model: n_theta set to 2
spotpython tuning: 7.295281981238084e-06 [#######---] 73.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 7.295281981238084e-06 [########--] 80.00% 
Anisotropic model: n_theta set to 2
spotpython tuning: 7.295281981238084e-06 [#########-] 86.67% 
Anisotropic model: n_theta set to 2
spotpython tuning: 7.295281981238084e-06 [#########-] 93.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 7.295281981238084e-06 [##########] 100.00% Done...

Experiment saved to 003_res.pkl
<spotpython.spot.spot.Spot at 0x158b96850>

The search progress of the optimization with the anisotropic model can be visualized:

spot_2_anisotropic.plot_progress(log_y=True)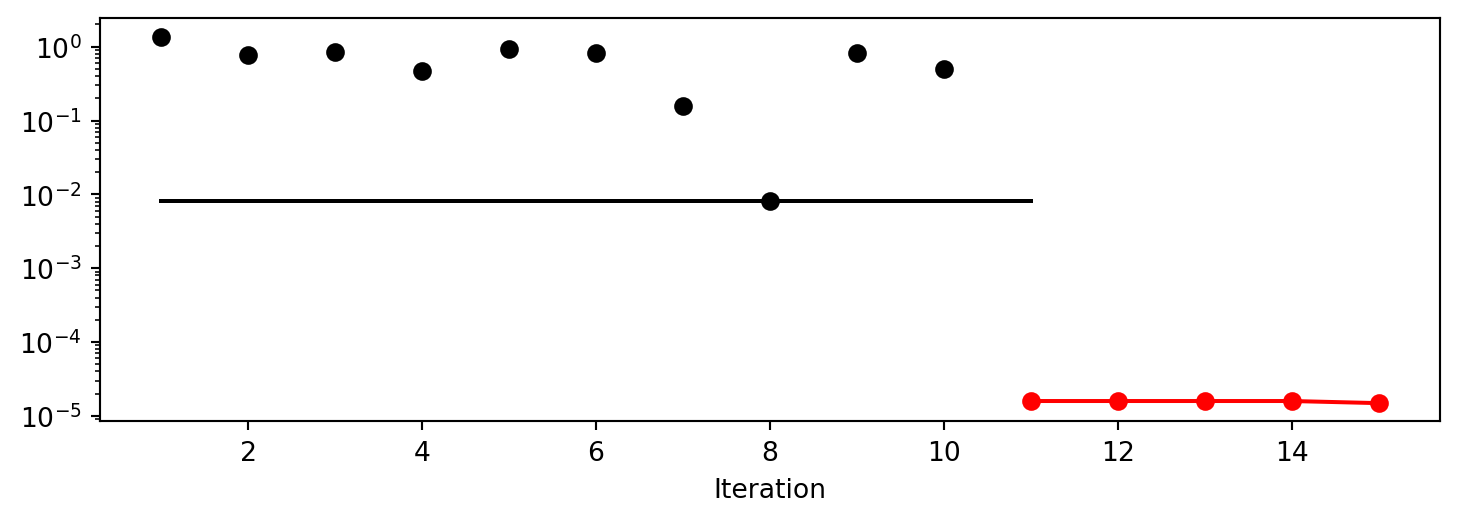

spot_2_anisotropic.print_results()
min y: 7.295281981238084e-06
x0: 0.0005342902641415708
x1: 0.0026476056909746993
[['x0', np.float64(0.0005342902641415708)],
 ['x1', np.float64(0.0026476056909746993)]]
spot_2_anisotropic.surrogate.plot()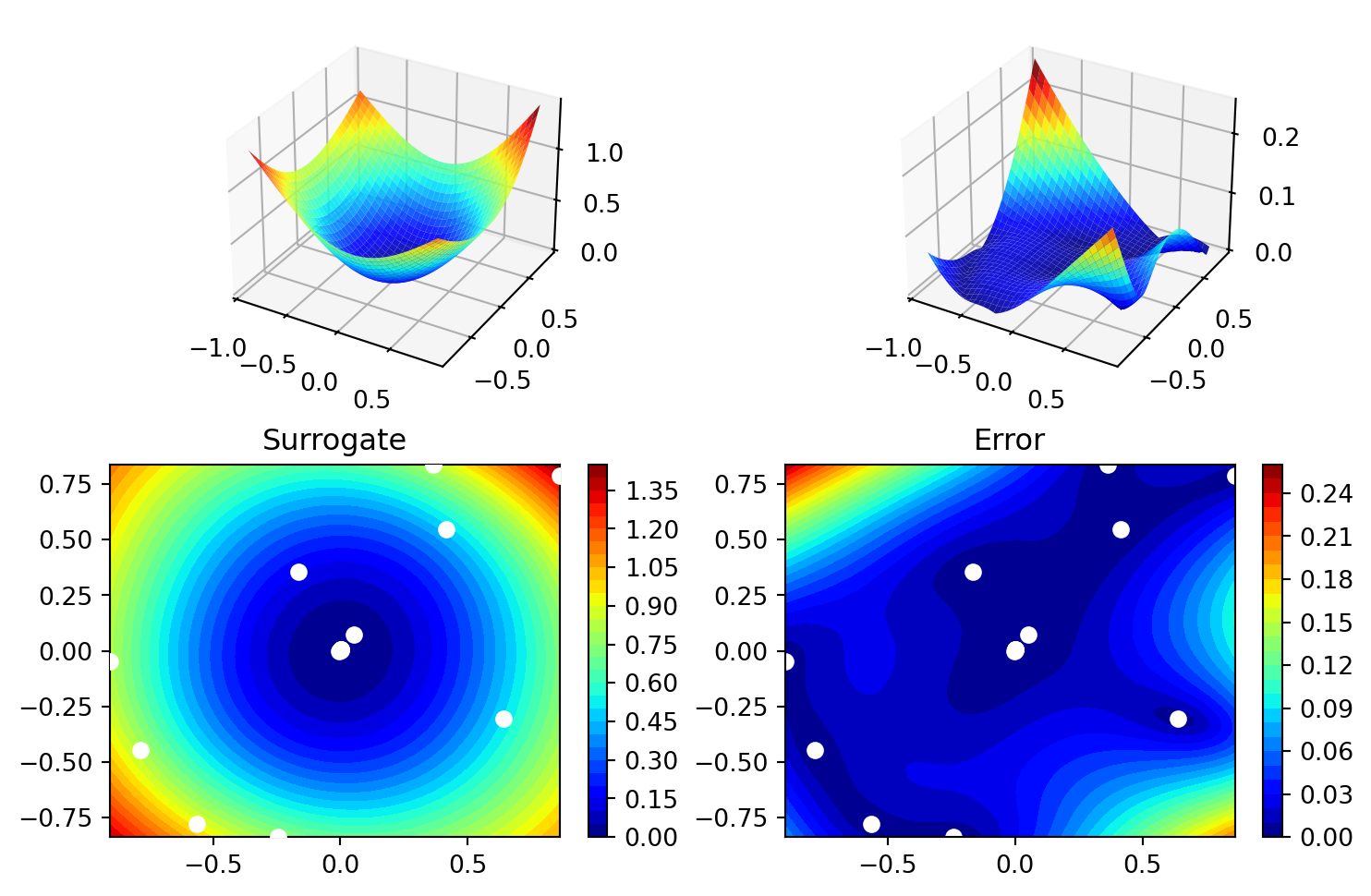

14.2.1 Taking a Look at the theta Values

14.2.1.1 theta Values from the spot Model

We can check, whether one or several theta values were used. The theta values from the surrogate can be printed as follows:

spot_2_anisotropic.surrogate.theta
array([-0.31281903, -0.13657863])
  • Since the surrogate from the isotropic setting was stored as spot_2, we can also take a look at the theta value from this model:
spot_2.surrogate.theta
array([-0.07437657])

14.2.1.2 TensorBoard

Now we can start TensorBoard in the background with the following command:

tensorboard --logdir="./runs"

We can access the TensorBoard web server with the following URL:

http://localhost:6006/

The TensorBoard plot illustrates how spotpython can be used as a microscope for the internal mechanisms of the surrogate-based optimization process. Here, one important parameter, the learning rate \(\theta\) of the Kriging surrogate is plotted against the number of optimization steps.

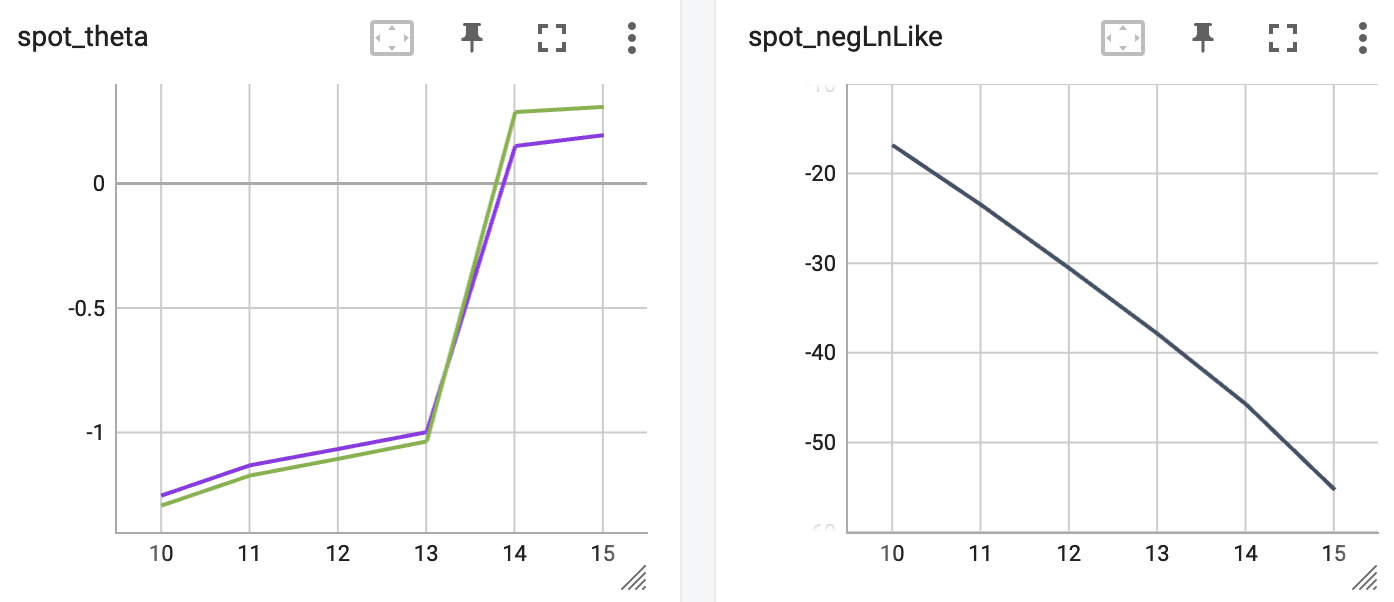
TensorBoard visualization of the spotpython surrogate model.

14.3 Exercises

14.3.1 1. The Branin Function fun_branin

  • Describe the function.
    • The input dimension is 2. The search range is \(-5 \leq x_1 \leq 10\) and \(0 \leq x_2 \leq 15\).
  • Compare the results from spotpython run a) with isotropic and b) anisotropic surrogate models.
  • Modify the termination criterion: instead of the number of evaluations (which is specified via fun_evals), the time should be used as the termination criterion. This can be done as follows (max_time=1 specifies a run time of one minute):
from math import inf
fun_control = fun_control_init(
              fun_evals=inf,
              max_time=1)

14.3.2 2. The Two-dimensional Sin-Cos Function fun_sin_cos

  • Describe the function.
    • The input dimension is 2. The search range is \(-2\pi \leq x_1 \leq 2\pi\) and \(-2\pi \leq x_2 \leq 2\pi\).
  • Compare the results from spotpython run a) with isotropic and b) anisotropic surrogate models.
  • Modify the termination criterion (max_time instead of fun_evals) as described for fun_branin.

14.3.3 3. The Two-dimensional Runge Function fun_runge

  • Describe the function.
    • The input dimension is 2. The search range is \(-5 \leq x_1 \leq 5\) and \(-5 \leq x_2 \leq 5\).
  • Compare the results from spotpython run a) with isotropic and b) anisotropic surrogate models.
  • Modify the termination criterion (max_time instead of fun_evals) as described for fun_branin.

14.3.4 4. The Ten-dimensional Wing-Weight Function fun_wingwt

  • Describe the function.
    • The input dimension is 10. The search ranges are between 0 and 1 (values are mapped internally to their natural bounds).
  • Compare the results from spotpython run a) with isotropic and b) anisotropic surrogate models.
  • Modify the termination criterion (max_time instead of fun_evals) as described for fun_branin.

14.3.5 5. The Two-dimensional Rosenbrock Function fun_rosen

  • Describe the function.
    • The input dimension is 2. The search ranges are between -5 and 10.
  • Compare the results from spotpython run a) with isotropic and b) anisotropic surrogate models.
  • Modify the termination criterion (max_time instead of fun_evals) as described for fun_branin.

14.4 Selected Solutions

14.4.1 Solution to Exercise Section 14.3.5: The Two-dimensional Rosenbrock Function fun_rosen

14.4.1.1 The Two Dimensional fun_rosen: The Isotropic Case

import numpy as np
from spotpython.fun.objectivefunctions import Analytical
from spotpython.utils.init import fun_control_init, surrogate_control_init
from spotpython.spot import Spot

The spotpython package provides several classes of objective functions. We will use the fun_rosen in the analytical class [SOURCE].

fun_rosen = Analytical().fun_rosen

Here we will use problem dimension \(k=2\), which can be specified by the lower bound arrays. The size of the lower bound array determines the problem dimension.

The prefix is set to "ROSEN" to distinguish the results from the one-dimensional case. Again, TensorBoard can be used to monitor the progress of the optimization.

fun_control = fun_control_init(
              PREFIX="ROSEN",
              lower = np.array([-5, -5]),
              upper = np.array([10, 10]),
              show_progress=True)
surrogate_control = surrogate_control_init(isotropic=True)
spot_rosen = Spot(fun=fun_rosen,
                  fun_control=fun_control,
                  surrogate_control=surrogate_control)
spot_rosen.run()
Isotropic model: n_theta set to 1
Isotropic model: n_theta set to 1
spotpython tuning: 53.73852099142873 [#######---] 73.33% 
Isotropic model: n_theta set to 1
spotpython tuning: 49.86693879440119 [########--] 80.00% 
Isotropic model: n_theta set to 1
spotpython tuning: 49.86693879440119 [#########-] 86.67% 
Isotropic model: n_theta set to 1
spotpython tuning: 12.621432319739265 [#########-] 93.33% 
Isotropic model: n_theta set to 1
spotpython tuning: 12.621432319739265 [##########] 100.00% Done...

Experiment saved to ROSEN_res.pkl
<spotpython.spot.spot.Spot at 0x15c02f250>
Note

Now we can start TensorBoard in the background with the following command:

tensorboard --logdir="./runs"

and can access the TensorBoard web server with the following URL:

http://localhost:6006/
14.4.1.1.1 Results
_ = spot_rosen.print_results()
min y: 12.621432319739265
x0: -0.539880707043816
x1: -0.7209615225332818
spot_rosen.plot_progress()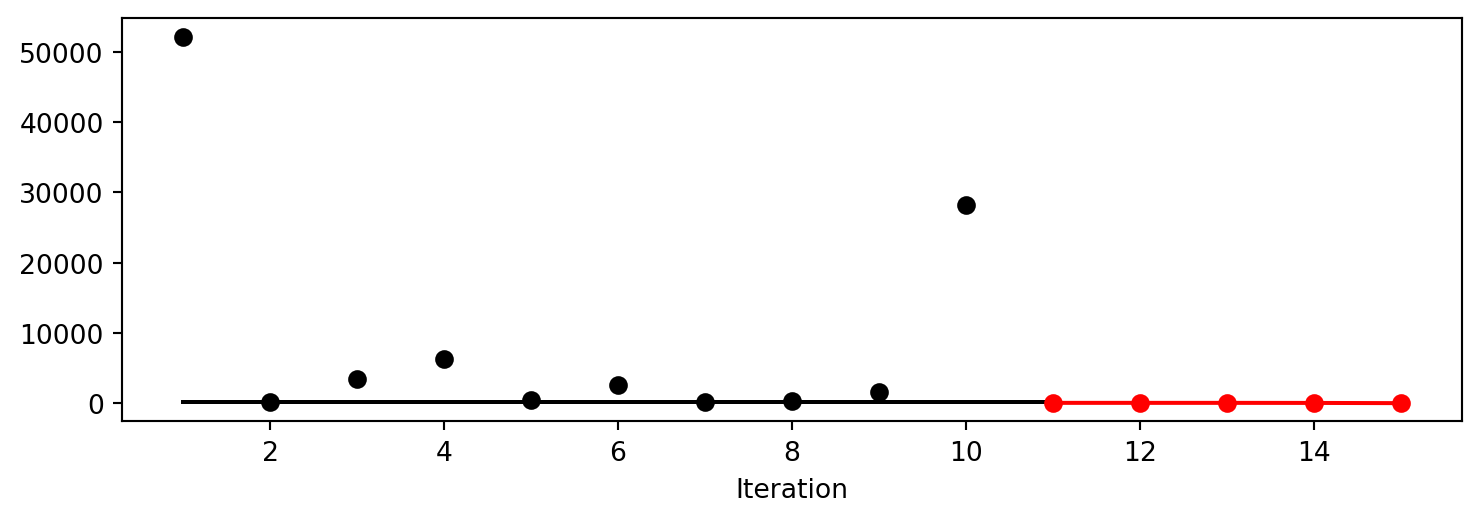

14.4.1.1.2 A Contour Plot

We can select two dimensions, say \(i=0\) and \(j=1\), and generate a contour plot as follows.

min_z = None
max_z = None
spot_rosen.plot_contour(i=0, j=1, min_z=min_z, max_z=max_z)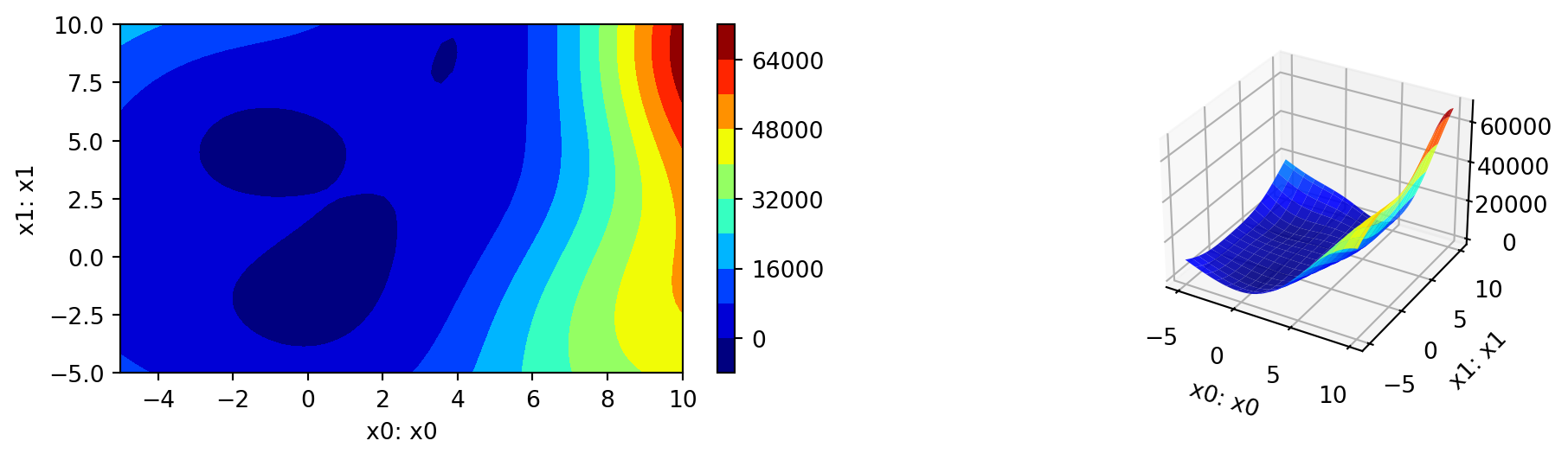

  • The variable importance cannot be calculated, because only one theta value was used.
14.4.1.1.3 TensorBoard

TBD

14.4.1.2 The Two Dimensional fun_rosen: The Anisotropic Case

import numpy as np
from spotpython.fun.objectivefunctions import Analytical
from spotpython.utils.init import fun_control_init, surrogate_control_init
from spotpython.spot import Spot

The spotpython package provides several classes of objective functions. We will use the fun_rosen in the analytical class [SOURCE].

fun_rosen = Analytical().fun_rosen

Here we will use problem dimension \(k=2\), which can be specified by the lower bound arrays. The size of the lower bound array determines the problem dimension. The default anisotropic kernel is used, so no isotropic parameter is set.

We can also add interpretable labels to the dimensions, which will be used in the plots.

fun_control = fun_control_init(
              PREFIX="ROSEN",
              lower = np.array([-5, -5]),
              upper = np.array([10, 10]),
              show_progress=True)
spot_rosen = Spot(fun=fun_rosen,
                  fun_control=fun_control)
spot_rosen.run()
Anisotropic model: n_theta set to 2
Anisotropic model: n_theta set to 2
spotpython tuning: 90.80194106348245 [#######---] 73.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 1.0168856465748572 [########--] 80.00% 
Anisotropic model: n_theta set to 2
spotpython tuning: 1.0168856465748572 [#########-] 86.67% 
Anisotropic model: n_theta set to 2
spotpython tuning: 1.0168856465748572 [#########-] 93.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 1.0168856465748572 [##########] 100.00% Done...

Experiment saved to ROSEN_res.pkl
<spotpython.spot.spot.Spot at 0x15d00ca50>
Note

Now we can start TensorBoard in the background with the following command:

tensorboard --logdir="./runs"

and can access the TensorBoard web server with the following URL:

http://localhost:6006/
14.4.1.2.1 Results
_ = spot_rosen.print_results()
min y: 1.0168856465748572
x0: 0.0027507471746656834
x1: -0.04729948816426377
spot_rosen.plot_progress()

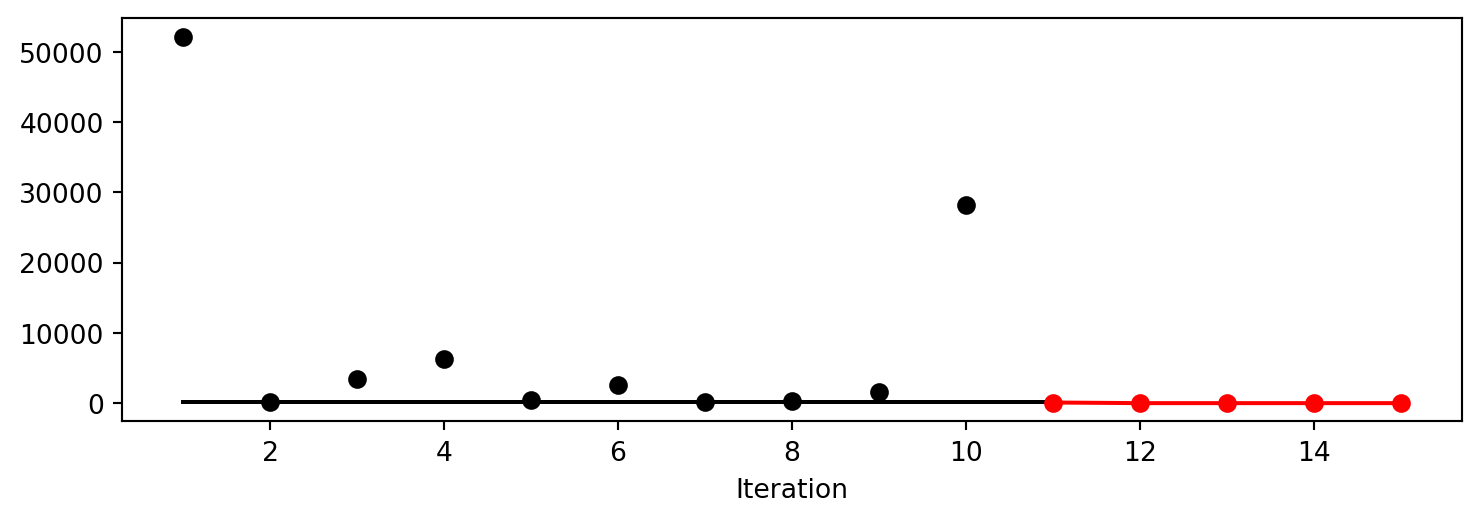
14.4.1.2.2 A Contour Plot

We can select two dimensions, say \(i=0\) and \(j=1\), and generate a contour plot as follows.

min_z = None
max_z = None
spot_rosen.plot_contour(i=0, j=1, min_z=min_z, max_z=max_z)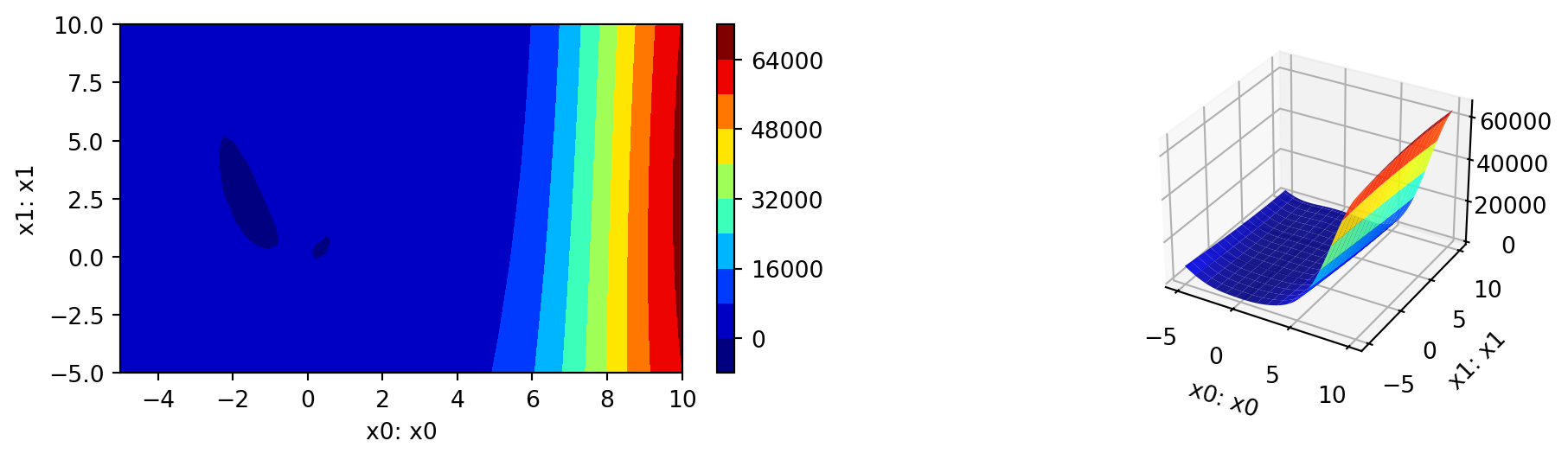

  • The variable importance can be calculated as follows:
_ = spot_rosen.print_importance()
x0:  100.0
x1:  2.2265675557846083
spot_rosen.plot_importance()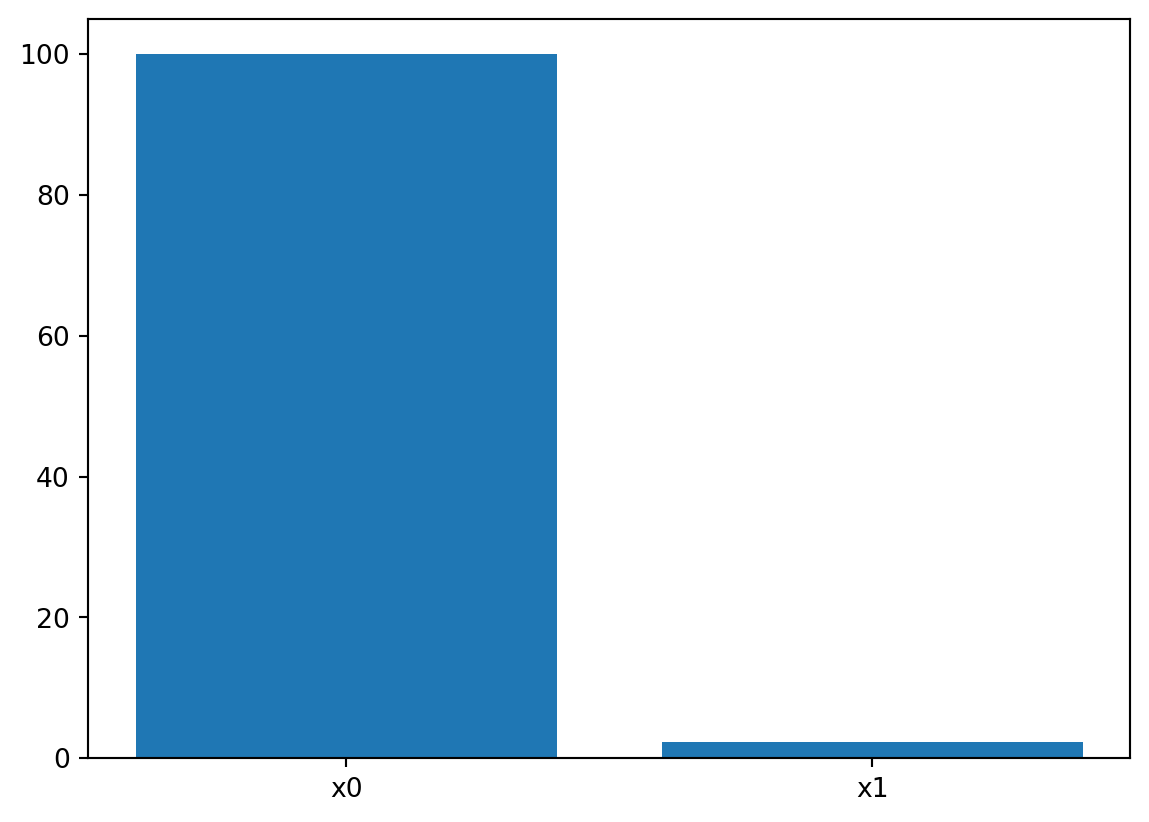

14.4.1.2.3 TensorBoard

TBD

14.5 Jupyter Notebook

Note