[57]{.chapter-number}  [Hyperparameter Tuning with `spotpython` and `PyTorch` Lightning Using a CondNet Model]{.chapter-title}

doi:10.48550/arXiv.2307.10262

57 Hyperparameter Tuning with `spotpython` and `PyTorch` Lightning Using a CondNet Model

We use the Diabetes dataset to illustrate the hyperparameter tuning process of a CondNet model using the spotpython package.
The CondNet model is a conditional neural network that can be used to model conditional distributions [LINK].

Note, the divergence_threshold is set to 5,000, which is based on some pre-experiments with the Diabetes data set.

from spotpython.data.diabetes import Diabetes
from spotpython.hyperdict.light_hyper_dict import LightHyperDict
from spotpython.fun.hyperlight import HyperLight
from spotpython.utils.init import (fun_control_init, surrogate_control_init, design_control_init)
from spotpython.utils.eda import print_exp_table
from spotpython.spot import Spot
from spotpython.utils.file import get_experiment_filename
from math import inf
from spotpython.hyperparameters.values import set_hyperparameter

PREFIX="CondNet_01"

data_set = Diabetes()
input_dim = 10
output_dim = 1
cond_dim = 2

fun_control = fun_control_init(
    PREFIX=PREFIX,
    fun_evals=inf,
    max_time=1,
    data_set = data_set,
    core_model_name="light.regression.NNCondNetRegressor",
    hyperdict=LightHyperDict,
    divergence_threshold=5_000,
    _L_in=input_dim - cond_dim,
    _L_out=1,
    _L_cond=cond_dim,)

fun = HyperLight().fun


set_hyperparameter(fun_control, "optimizer", [ "Adadelta", "Adam", "Adamax"])
set_hyperparameter(fun_control, "l1", [3,4])
set_hyperparameter(fun_control, "epochs", [3,7])
set_hyperparameter(fun_control, "batch_size", [4,5])
set_hyperparameter(fun_control, "dropout_prob", [0.0, 0.025])
set_hyperparameter(fun_control, "patience", [2,3])
set_hyperparameter(fun_control, "lr_mult", [0.1, 20.0])

design_control = design_control_init(init_size=10)

print_exp_table(fun_control)

module_name: light
submodule_name: regression
model_name: NNCondNetRegressor
| name           | type   | default   |   lower |   upper | transform             |
|----------------|--------|-----------|---------|---------|-----------------------|
| l1             | int    | 3         |     3   |   4     | transform_power_2_int |
| epochs         | int    | 4         |     3   |   7     | transform_power_2_int |
| batch_size     | int    | 4         |     4   |   5     | transform_power_2_int |
| act_fn         | factor | ReLU      |     0   |   5     | None                  |
| optimizer      | factor | SGD       |     0   |   2     | None                  |
| dropout_prob   | float  | 0.01      |     0   |   0.025 | None                  |
| lr_mult        | float  | 1.0       |     0.1 |  20     | None                  |
| patience       | int    | 2         |     2   |   3     | transform_power_2_int |
| batch_norm     | factor | 0         |     0   |   1     | None                  |
| initialization | factor | Default   |     0   |   4     | None                  |

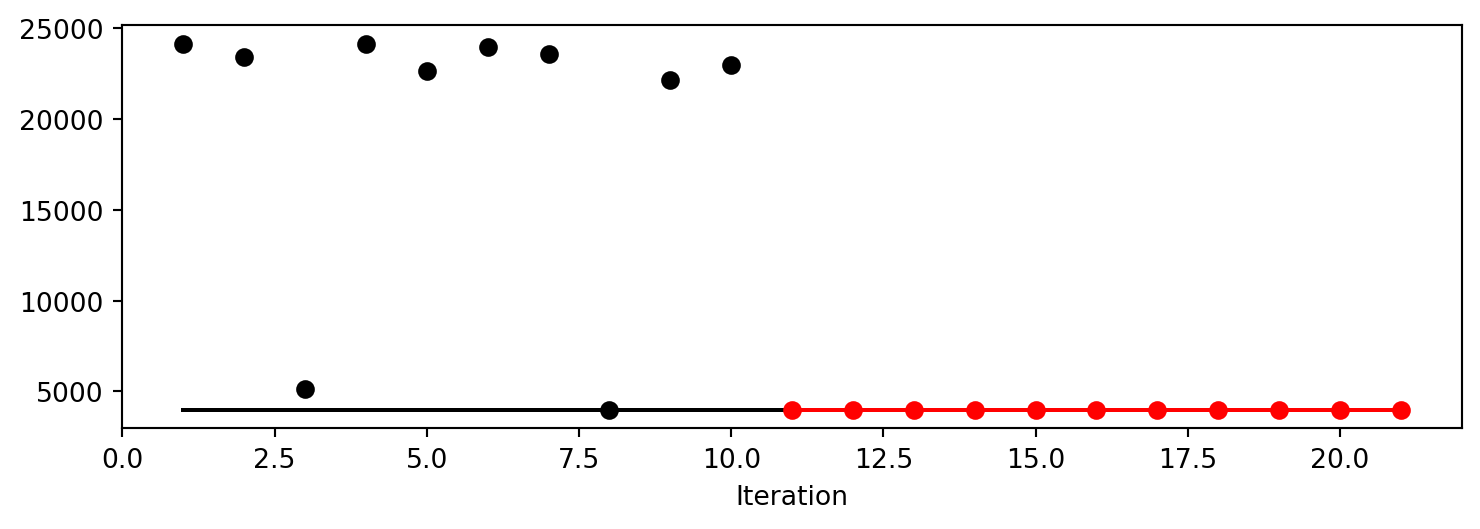
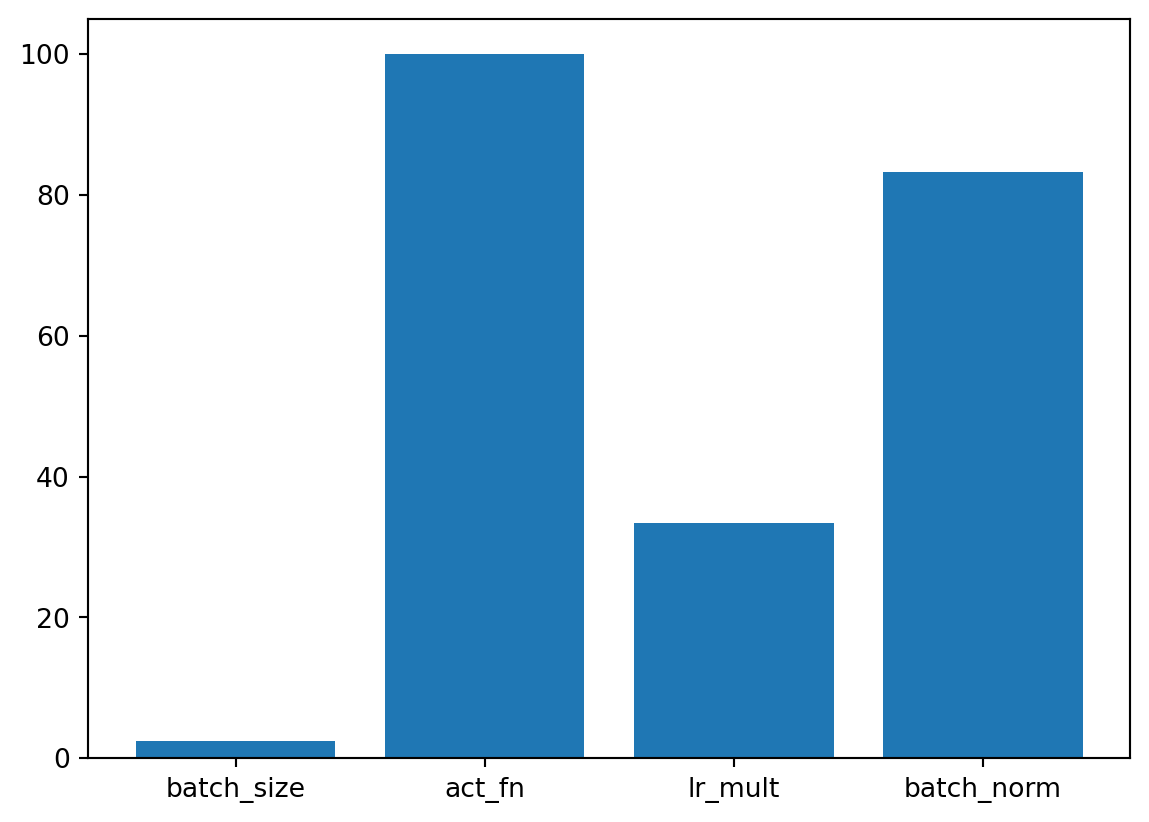
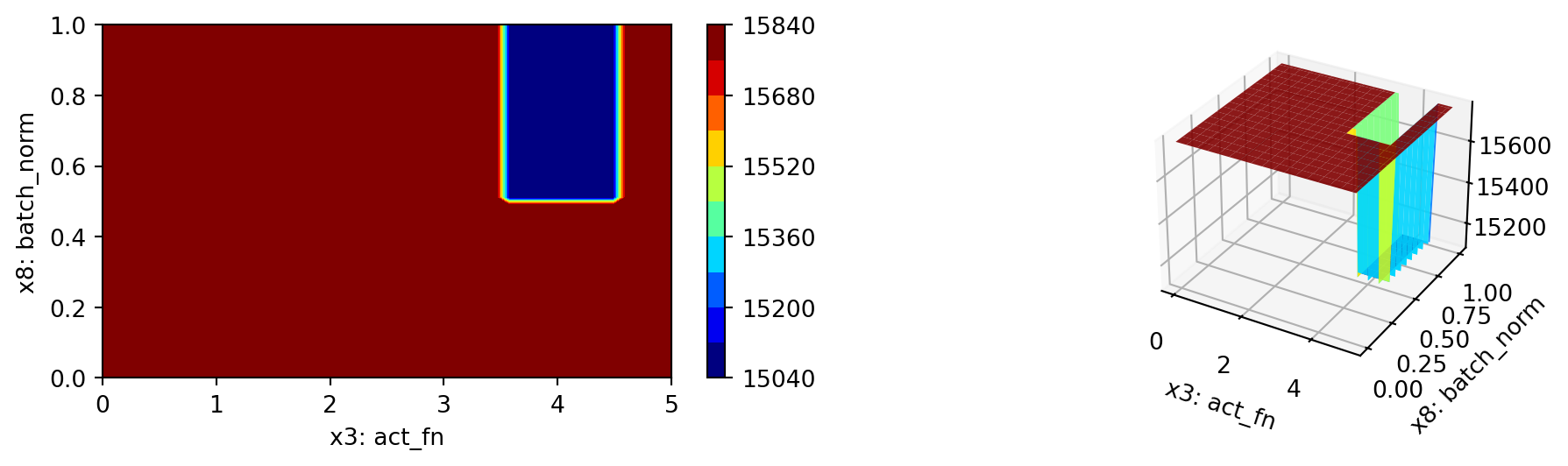
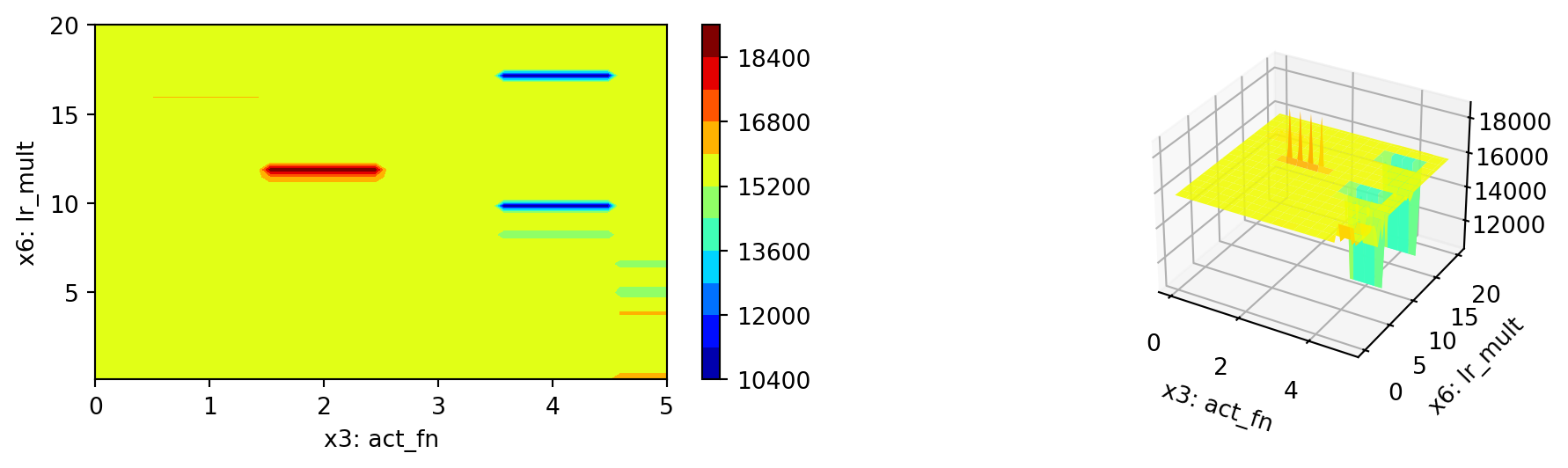
spot_tuner = Spot(fun=fun,fun_control=fun_control, design_control=design_control)
res = spot_tuner.run()

train_model result: {'val_loss': 24266.927734375, 'hp_metric': 24266.927734375}

train_model result: {'val_loss': 24001.298828125, 'hp_metric': 24001.298828125}

train_model result: {'val_loss': 21142.806640625, 'hp_metric': 21142.806640625}

train_model result: {'val_loss': 24029.455078125, 'hp_metric': 24029.455078125}

train_model result: {'val_loss': 23382.876953125, 'hp_metric': 23382.876953125}

train_model result: {'val_loss': 24010.201171875, 'hp_metric': 24010.201171875}
train_model result: {'val_loss': 23698.623046875, 'hp_metric': 23698.623046875}

train_model result: {'val_loss': 23921.46484375, 'hp_metric': 23921.46484375}
train_model result: {'val_loss': 23699.216796875, 'hp_metric': 23699.216796875}

train_model result: {'val_loss': 24038.666015625, 'hp_metric': 24038.666015625}

train_model result: {'val_loss': 22806.115234375, 'hp_metric': 22806.115234375}
spotpython tuning: 21142.806640625 [----------] 0.67%

train_model result: {'val_loss': 8619.9912109375, 'hp_metric': 8619.9912109375}
spotpython tuning: 8619.9912109375 [----------] 1.31%

train_model result: {'val_loss': nan, 'hp_metric': nan}
train_model result: {'val_loss': 21551.88671875, 'hp_metric': 21551.88671875}
spotpython tuning: 8619.9912109375 [----------] 2.68%

train_model result: {'val_loss': 22208.6953125, 'hp_metric': 22208.6953125}
spotpython tuning: 8619.9912109375 [----------] 3.88%

train_model result: {'val_loss': 24025.337890625, 'hp_metric': 24025.337890625}
spotpython tuning: 8619.9912109375 [----------] 4.29%

train_model result: {'val_loss': 23826.326171875, 'hp_metric': 23826.326171875}
spotpython tuning: 8619.9912109375 [----------] 4.89%

train_model result: {'val_loss': 23540.75390625, 'hp_metric': 23540.75390625}
spotpython tuning: 8619.9912109375 [#---------] 5.52%

train_model result: {'val_loss': 23834.033203125, 'hp_metric': 23834.033203125}
spotpython tuning: 8619.9912109375 [#---------] 6.80%

train_model result: {'val_loss': 23013.712890625, 'hp_metric': 23013.712890625}
spotpython tuning: 8619.9912109375 [#---------] 7.24%

train_model result: {'val_loss': 23815.0703125, 'hp_metric': 23815.0703125}
spotpython tuning: 8619.9912109375 [#---------] 8.14%

train_model result: {'val_loss': 23997.41015625, 'hp_metric': 23997.41015625}
spotpython tuning: 8619.9912109375 [#---------] 9.16%

train_model result: {'val_loss': 24022.275390625, 'hp_metric': 24022.275390625}
spotpython tuning: 8619.9912109375 [#---------] 10.12%

train_model result: {'val_loss': 23983.48828125, 'hp_metric': 23983.48828125}
spotpython tuning: 8619.9912109375 [#---------] 11.00%

train_model result: {'val_loss': nan, 'hp_metric': nan}

train_model result: {'val_loss': 24106.548828125, 'hp_metric': 24106.548828125}
spotpython tuning: 8619.9912109375 [#---------] 11.89%

train_model result: {'val_loss': 49646.796875, 'hp_metric': 49646.796875}
spotpython tuning: 8619.9912109375 [#---------] 12.70%

train_model result: {'val_loss': 17103.455078125, 'hp_metric': 17103.455078125}
spotpython tuning: 8619.9912109375 [#---------] 14.30%

train_model result: {'val_loss': 23756.97265625, 'hp_metric': 23756.97265625}
spotpython tuning: 8619.9912109375 [##--------] 15.13%

train_model result: {'val_loss': 24038.849609375, 'hp_metric': 24038.849609375}
spotpython tuning: 8619.9912109375 [##--------] 16.19%

train_model result: {'val_loss': 23411.689453125, 'hp_metric': 23411.689453125}
spotpython tuning: 8619.9912109375 [##--------] 17.38%

train_model result: {'val_loss': 23974.251953125, 'hp_metric': 23974.251953125}
spotpython tuning: 8619.9912109375 [##--------] 18.60%

train_model result: {'val_loss': 22355.33984375, 'hp_metric': 22355.33984375}
spotpython tuning: 8619.9912109375 [##--------] 19.64%

train_model result: {'val_loss': 23605.009765625, 'hp_metric': 23605.009765625}
spotpython tuning: 8619.9912109375 [##--------] 21.04%

train_model result: {'val_loss': 23662.984375, 'hp_metric': 23662.984375}
spotpython tuning: 8619.9912109375 [##--------] 21.90%

train_model result: {'val_loss': 23848.388671875, 'hp_metric': 23848.388671875}
spotpython tuning: 8619.9912109375 [##--------] 23.14%

train_model result: {'val_loss': 20449.564453125, 'hp_metric': 20449.564453125}
spotpython tuning: 8619.9912109375 [##--------] 24.08%

train_model result: {'val_loss': 24015.919921875, 'hp_metric': 24015.919921875}
spotpython tuning: 8619.9912109375 [###-------] 25.25%

train_model result: {'val_loss': 22477.537109375, 'hp_metric': 22477.537109375}
spotpython tuning: 8619.9912109375 [###-------] 26.34%

train_model result: {'val_loss': 23313.23046875, 'hp_metric': 23313.23046875}
spotpython tuning: 8619.9912109375 [###-------] 27.28%

train_model result: {'val_loss': 24074.498046875, 'hp_metric': 24074.498046875}
spotpython tuning: 8619.9912109375 [###-------] 28.28%

train_model result: {'val_loss': 24013.283203125, 'hp_metric': 24013.283203125}
spotpython tuning: 8619.9912109375 [###-------] 29.26%

train_model result: {'val_loss': 23852.30859375, 'hp_metric': 23852.30859375}
spotpython tuning: 8619.9912109375 [###-------] 30.34%

train_model result: {'val_loss': 24025.47265625, 'hp_metric': 24025.47265625}
spotpython tuning: 8619.9912109375 [###-------] 31.55%

train_model result: {'val_loss': nan, 'hp_metric': nan}
train_model result: {'val_loss': 23986.77734375, 'hp_metric': 23986.77734375}
spotpython tuning: 8619.9912109375 [###-------] 32.58%

train_model result: {'val_loss': 23229.576171875, 'hp_metric': 23229.576171875}
spotpython tuning: 8619.9912109375 [###-------] 33.47%

train_model result: {'val_loss': 24005.08203125, 'hp_metric': 24005.08203125}
spotpython tuning: 8619.9912109375 [####------] 35.26%

train_model result: {'val_loss': 23995.12109375, 'hp_metric': 23995.12109375}
spotpython tuning: 8619.9912109375 [####------] 36.45%

train_model result: {'val_loss': 23407.36328125, 'hp_metric': 23407.36328125}
spotpython tuning: 8619.9912109375 [####------] 37.39%

train_model result: {'val_loss': 21608.36328125, 'hp_metric': 21608.36328125}
spotpython tuning: 8619.9912109375 [####------] 38.48%

train_model result: {'val_loss': 24038.30859375, 'hp_metric': 24038.30859375}
spotpython tuning: 8619.9912109375 [####------] 39.27%

train_model result: {'val_loss': 16329.5380859375, 'hp_metric': 16329.5380859375}
spotpython tuning: 8619.9912109375 [####------] 40.24%

train_model result: {'val_loss': 23951.35546875, 'hp_metric': 23951.35546875}
spotpython tuning: 8619.9912109375 [####------] 41.27%

train_model result: {'val_loss': 11439.685546875, 'hp_metric': 11439.685546875}
spotpython tuning: 8619.9912109375 [####------] 42.12%

train_model result: {'val_loss': 22839.025390625, 'hp_metric': 22839.025390625}
spotpython tuning: 8619.9912109375 [####------] 43.21%

train_model result: {'val_loss': nan, 'hp_metric': nan}
train_model result: {'val_loss': 24041.166015625, 'hp_metric': 24041.166015625}
spotpython tuning: 8619.9912109375 [####------] 44.68%

train_model result: {'val_loss': 24066.73046875, 'hp_metric': 24066.73046875}
spotpython tuning: 8619.9912109375 [#####-----] 45.88%

train_model result: {'val_loss': 18074.28125, 'hp_metric': 18074.28125}
spotpython tuning: 8619.9912109375 [#####-----] 47.79%

train_model result: {'val_loss': 23881.76953125, 'hp_metric': 23881.76953125}
spotpython tuning: 8619.9912109375 [#####-----] 48.62%

train_model result: {'val_loss': 23629.091796875, 'hp_metric': 23629.091796875}
spotpython tuning: 8619.9912109375 [#####-----] 50.40%

train_model result: {'val_loss': 23373.52734375, 'hp_metric': 23373.52734375}
spotpython tuning: 8619.9912109375 [#####-----] 51.18%

train_model result: {'val_loss': 23675.16015625, 'hp_metric': 23675.16015625}
spotpython tuning: 8619.9912109375 [#####-----] 52.78%

train_model result: {'val_loss': 14002.791015625, 'hp_metric': 14002.791015625}
spotpython tuning: 8619.9912109375 [#####-----] 54.48%

train_model result: {'val_loss': 23436.626953125, 'hp_metric': 23436.626953125}
spotpython tuning: 8619.9912109375 [######----] 55.43%

train_model result: {'val_loss': 23869.771484375, 'hp_metric': 23869.771484375}
spotpython tuning: 8619.9912109375 [######----] 57.00%

train_model result: {'val_loss': 23896.365234375, 'hp_metric': 23896.365234375}
spotpython tuning: 8619.9912109375 [######----] 58.47%

train_model result: {'val_loss': 23505.419921875, 'hp_metric': 23505.419921875}
spotpython tuning: 8619.9912109375 [######----] 59.69%

train_model result: {'val_loss': 20871.89453125, 'hp_metric': 20871.89453125}
spotpython tuning: 8619.9912109375 [######----] 60.71%

train_model result: {'val_loss': 23979.95703125, 'hp_metric': 23979.95703125}
spotpython tuning: 8619.9912109375 [######----] 62.06%

train_model result: {'val_loss': 24059.26953125, 'hp_metric': 24059.26953125}
spotpython tuning: 8619.9912109375 [######----] 63.60%

train_model result: {'val_loss': 10945.1630859375, 'hp_metric': 10945.1630859375}
spotpython tuning: 8619.9912109375 [######----] 64.75%

train_model result: {'val_loss': 99476.9453125, 'hp_metric': 99476.9453125}
spotpython tuning: 8619.9912109375 [#######---] 65.87%

train_model result: {'val_loss': 17536.15625, 'hp_metric': 17536.15625}
spotpython tuning: 8619.9912109375 [#######---] 67.32%

train_model result: {'val_loss': 24091.85546875, 'hp_metric': 24091.85546875}
spotpython tuning: 8619.9912109375 [#######---] 68.40%

train_model result: {'val_loss': 23771.462890625, 'hp_metric': 23771.462890625}
spotpython tuning: 8619.9912109375 [#######---] 70.27%

train_model result: {'val_loss': 5873.17529296875, 'hp_metric': 5873.17529296875}
spotpython tuning: 5873.17529296875 [#######---] 71.08%

train_model result: {'val_loss': 24041.21484375, 'hp_metric': 24041.21484375}
spotpython tuning: 5873.17529296875 [#######---] 72.23%

train_model result: {'val_loss': 21957.83984375, 'hp_metric': 21957.83984375}
spotpython tuning: 5873.17529296875 [#######---] 74.14%

train_model result: {'val_loss': 9341.4580078125, 'hp_metric': 9341.4580078125}
spotpython tuning: 5873.17529296875 [########--] 75.61%

train_model result: {'val_loss': 23288.216796875, 'hp_metric': 23288.216796875}
spotpython tuning: 5873.17529296875 [########--] 76.22%

train_model result: {'val_loss': 23986.6484375, 'hp_metric': 23986.6484375}
spotpython tuning: 5873.17529296875 [########--] 77.38%

train_model result: {'val_loss': 23628.93359375, 'hp_metric': 23628.93359375}
spotpython tuning: 5873.17529296875 [########--] 78.45%

train_model result: {'val_loss': 23139.828125, 'hp_metric': 23139.828125}
spotpython tuning: 5873.17529296875 [########--] 79.56%

train_model result: {'val_loss': 20805.08203125, 'hp_metric': 20805.08203125}
spotpython tuning: 5873.17529296875 [########--] 82.20%

train_model result: {'val_loss': 24000.859375, 'hp_metric': 24000.859375}
spotpython tuning: 5873.17529296875 [########--] 83.71%

train_model result: {'val_loss': 24102.216796875, 'hp_metric': 24102.216796875}
spotpython tuning: 5873.17529296875 [########--] 84.50%

train_model result: {'val_loss': 22739.958984375, 'hp_metric': 22739.958984375}
spotpython tuning: 5873.17529296875 [#########-] 85.94%

train_model result: {'val_loss': 23866.486328125, 'hp_metric': 23866.486328125}
spotpython tuning: 5873.17529296875 [#########-] 86.91%

train_model result: {'val_loss': 24045.50390625, 'hp_metric': 24045.50390625}
spotpython tuning: 5873.17529296875 [#########-] 88.93%

train_model result: {'val_loss': 23930.2265625, 'hp_metric': 23930.2265625}
spotpython tuning: 5873.17529296875 [#########-] 89.85%

train_model result: {'val_loss': 23717.611328125, 'hp_metric': 23717.611328125}
spotpython tuning: 5873.17529296875 [#########-] 91.35%

train_model result: {'val_loss': 24002.287109375, 'hp_metric': 24002.287109375}
spotpython tuning: 5873.17529296875 [#########-] 93.01%

train_model result: {'val_loss': 23766.0, 'hp_metric': 23766.0}
spotpython tuning: 5873.17529296875 [#########-] 94.75%

train_model result: {'val_loss': 24210.98828125, 'hp_metric': 24210.98828125}
spotpython tuning: 5873.17529296875 [##########] 96.92%

train_model result: {'val_loss': 19020.130859375, 'hp_metric': 19020.130859375}
spotpython tuning: 5873.17529296875 [##########] 98.07%

train_model result: {'val_loss': 23926.23046875, 'hp_metric': 23926.23046875}
spotpython tuning: 5873.17529296875 [##########] 99.03%

train_model result: {'val_loss': 19521.087890625, 'hp_metric': 19521.087890625}
spotpython tuning: 5873.17529296875 [##########] 100.00% Done...

Experiment saved to CondNet_01_res.pkl

57.1 Looking at the Results

57.1.1 Tuning Progress

After the hyperparameter tuning run is finished, the progress of the hyperparameter tuning can be visualized with spotpython’s method plot_progress. The black points represent the performace values (score or metric) of hyperparameter configurations from the initial design, whereas the red points represents the hyperparameter configurations found by the surrogate model based optimization.

spot_tuner.plot_progress()

57.1.2 Tuned Hyperparameters and Their Importance

Results can be printed in tabular form.

from spotpython.utils.eda import print_res_table
print_res_table(spot_tuner)

| name           | type   | default   |   lower |   upper | tuned                | transform             |   importance | stars   |
|----------------|--------|-----------|---------|---------|----------------------|-----------------------|--------------|---------|
| l1             | int    | 3         |     3.0 |     4.0 | 4.0                  | transform_power_2_int |         0.00 |         |
| epochs         | int    | 4         |     3.0 |     7.0 | 6.0                  | transform_power_2_int |         0.00 |         |
| batch_size     | int    | 4         |     4.0 |     5.0 | 4.0                  | transform_power_2_int |        41.16 | *       |
| act_fn         | factor | ReLU      |     0.0 |     5.0 | ELU                  | None                  |         0.01 |         |
| optimizer      | factor | SGD       |     0.0 |     2.0 | Adadelta             | None                  |         0.00 |         |
| dropout_prob   | float  | 0.01      |     0.0 |   0.025 | 0.012896809526746529 | None                  |         0.00 |         |
| lr_mult        | float  | 1.0       |     0.1 |    20.0 | 16.613974036489935   | None                  |         2.98 | *       |
| patience       | int    | 2         |     2.0 |     3.0 | 2.0                  | transform_power_2_int |         0.00 |         |
| batch_norm     | factor | 0         |     0.0 |     1.0 | 0                    | None                  |       100.00 | ***     |
| initialization | factor | Default   |     0.0 |     4.0 | kaiming_uniform      | None                  |         0.04 |         |

A histogram can be used to visualize the most important hyperparameters.

spot_tuner.plot_importance(threshold=1.0)

spot_tuner.plot_important_hyperparameter_contour(max_imp=3)

l1:  0.0033872747893603085
epochs:  0.0033872747893603085
batch_size:  41.15627143406879
act_fn:  0.01102208618745415
optimizer:  0.0033872747893603085
dropout_prob:  0.0033872747893603085
lr_mult:  2.9847017472621635
patience:  0.0033872747893603085
batch_norm:  100.0
initialization:  0.0439706551753409

57.1.3 Get the Tuned Architecture

import pprint
from spotpython.hyperparameters.values import get_tuned_architecture
config = get_tuned_architecture(spot_tuner)
pprint.pprint(config)

{'act_fn': ELU(),
 'batch_norm': False,
 'batch_size': 16,
 'dropout_prob': 0.012896809526746529,
 'epochs': 64,
 'initialization': 'kaiming_uniform',
 'l1': 16,
 'lr_mult': 16.613974036489935,
 'optimizer': 'Adadelta',
 'patience': 4}