23  User-Specified Functions: Extending the Analytical Class

This chapter illustrates how user-specified functions can be optimized and analyzed. It covers singe-objective function in Section 23.2 and multi-objective functions in Section 23.6, and how to use the spotpython package to optimize them. It shows a simple approach to define a user-specified function, both for single- and multi-objective optimization, and how to extend the Analytical class to create a custom function.

NoteCitation
  • If this document has been useful to you and you wish to cite it in a scientific publication, please refer to the following paper, which can be found on arXiv: https://arxiv.org/abs/2307.10262.
@ARTICLE{bart23iArXiv,
      author = {{Bartz-Beielstein}, Thomas},
      title = "{Hyperparameter Tuning Cookbook:
          A guide for scikit-learn, PyTorch, river, and spotpython}",
     journal = {arXiv e-prints},
    keywords = {Computer Science - Machine Learning,
      Computer Science - Artificial Intelligence, 90C26, I.2.6, G.1.6},
         year = 2023,
        month = jul,
          eid = {arXiv:2307.10262},
          doi = {10.48550/arXiv.2307.10262},
archivePrefix = {arXiv},
       eprint = {2307.10262},
 primaryClass = {cs.LG}
}

23.1 Software Requirements

  • The code examples in this chapter require the spotpython package, which can be installed via pip.
  • Furthermore, the following Python packages are required:
import numpy as np
import matplotlib.pyplot as plt
from spotpython.fun.objectivefunctions import Analytical
from spotpython.utils.init import fun_control_init, surrogate_control_init
from spotpython.spot import Spot

23.2 The Single-Objective Function: User Specified

We will use an analytical objective function, i.e., a function that can be described by a (closed) formula: \[ f(x) = \sum_i^k x_i^4. \]

This function is continuous, convex and unimodal. Since it returns one value for each input vector, it is a single-objective function. Multiple-objective functions can also be handled by spotpython. They are covered in Section 23.6.

The global minimum of the single-objective function is \[ f(x) = 0, \text{at } x = (0,0, \ldots, 0). \]

It can be implemented in Python as follows:

def user_fun(X):
    return(np.sum((X) **4, axis=1))

For example, if we have \(X = (1, 2, 3)\), then \[ f(x) = 1^4 + 2^4 + 3^4 = 1 + 16 + 81 = 98, \] and if we have \(X = (4, 5, 6)\), then \[ f(x) = 4^4 + 5^4 + 6^4 = 256 + 625 + 1296 = 2177. \]

We can pass a 2D array to the function, and it will return a 1D array with the results for each row:

user_fun(np.array([[1, 2, 3], [4, 5, 6]]))
array([  98, 2177])

To make user_fun compatible with the spotpython package, we need to extend its argument list, so that it can handle the fun_control dictionary.

def user_fun(X, fun_control=None):
    return(np.sum((X) **4, axis=1))

Alternatively, you can add the **kwargs argument to the function, which will allow you to pass any additional keyword arguments:

def user_fun(X, **kwargs):
    return(np.sum((X) **4, axis=1))
fun_control = fun_control_init(
              lower = np.array( [-1, -1]),
              upper = np.array([1, 1]),
)
S = Spot(fun=user_fun,
                 fun_control=fun_control)
S.run()
S.plot_progress()
Anisotropic model: n_theta set to 2
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [#######---] 73.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [########--] 80.00% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [#########-] 86.67% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [#########-] 93.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [##########] 100.00% Done...

Experiment saved to 000_res.pkl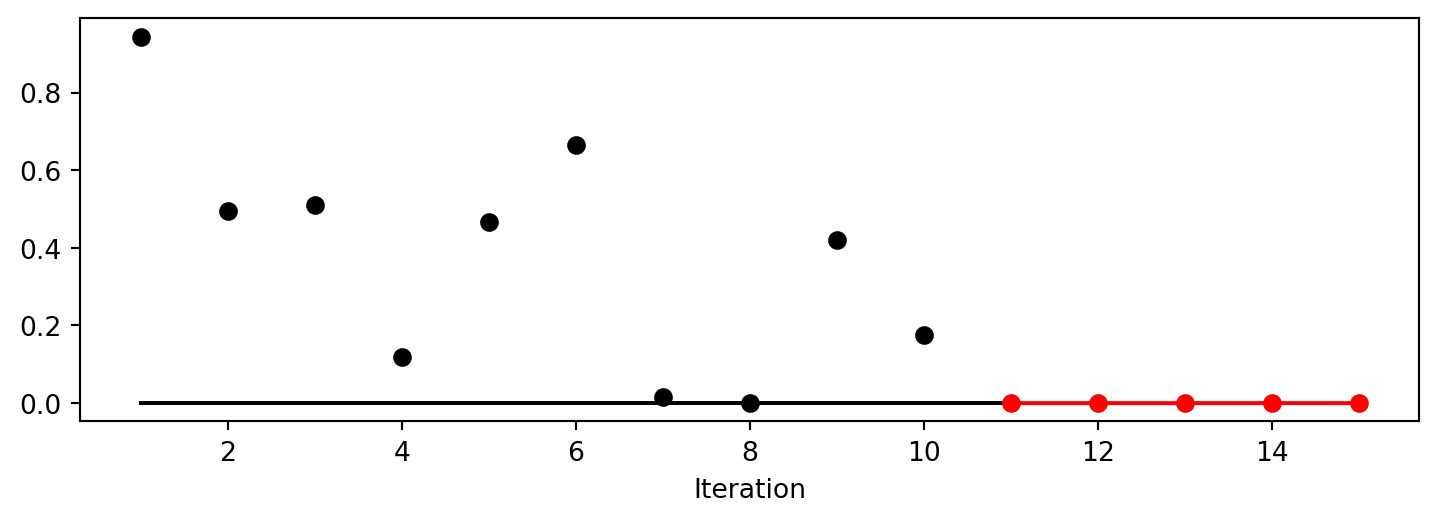

NoteSummary: Using spotpython with Single-Objective User-Specified Functions
  • spotpython accepts user-specified functions that can be defined in Python.
  • The function should accept a 2D array as input and return a 1D array as output.
  • The function can be defined with an additional argument fun_control to handle control parameters.
  • The fun_control dictionary can be initialized with the fun_control_init function, which allows you to specify the bounds of the input variables.

23.3 The Objective Function: Extending the Analytical Class

  • The Analytical class is a base class for analytical functions in the spotpython package.
  • It provides a framework for defining and evaluating analytical functions, including the ability to add noise to the output.
  • The Analytical class can be extended as follows:
from typing import Optional, Dict

class UserAnalytical(Analytical):
    def fun_user_function(self, X: np.ndarray, fun_control: Optional[Dict] = None) -> np.ndarray:
        """
        Custom new function: f(x) = x^4
        
        Args:
            X (np.ndarray): Input data as a 2D array.
            fun_control (Optional[Dict]): Control parameters for the function.
        
        Returns:
            np.ndarray: Computed values with optional noise.
        
        Examples:
            >>> import numpy as np
            >>> X = np.array([[1, 2, 3], [4, 5, 6]])
            >>> fun = UserAnalytical()
            >>> fun.fun_user_function(X)
        """
        X = self._prepare_input_data(X, fun_control)
     
        offset = np.ones(X.shape[1]) * self.offset
        y = np.sum((X - offset) **4, axis=1) 

        # Add noise if specified in fun_control
        return self._add_noise(y)
  • In comparison to the user_fun function, the UserAnalytical class provides additional functionality, such as adding noise to the output and preparing the input data.
  • First, we use the user_fun function as above.
user_fun = UserAnalytical()
X = np.array([[0, 0, 0], [1, 1, 1]])
results = user_fun.fun_user_function(X)
print(results)
[0. 3.]
  • Then we can add an offset to the function, which will shift the function by a constant value. This is useful for testing the optimization algorithm’s ability to find the global minimum.
user_fun = UserAnalytical(offset=1.0)
X = np.array([[0, 0, 0], [1, 1, 1]])
results = user_fun.fun_user_function(X)
print(results)
[3. 0.]
  • And, we can add noise to the function, which will add a random value to the output. This is useful for testing the optimization algorithm’s ability to find the global minimum in the presence of noise.
user_fun = UserAnalytical(sigma=1.0)
X = np.array([[0, 0, 0], [1, 1, 1]])
results = user_fun.fun_user_function(X)
print(results)
[0.06691138 3.11495313]
  • Here is an example of how to use the UserAnalytical class with the spotpython package:
user_fun = UserAnalytical().fun_user_function
fun_control = fun_control_init(
              PREFIX="USER",              
              lower = -1.0*np.ones(2),
              upper = np.ones(2),
              var_name=["User Pressure", "User Temp"],
              TENSORBOARD_CLEAN=True,
              tensorboard_log=True)
spot_user = Spot(fun=user_fun,
                  fun_control=fun_control)
spot_user.run()
Moving TENSORBOARD_PATH: runs/ to TENSORBOARD_PATH_OLD: runs_OLD/runs_2025_10_19_20_38_20_0
Created spot_tensorboard_path: runs/spot_logs/USER_maans08_2025-10-19_20-38-20 for SummaryWriter()
Anisotropic model: n_theta set to 2
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [#######---] 73.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [########--] 80.00% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [#########-] 86.67% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [#########-] 93.33% 
Anisotropic model: n_theta set to 2
spotpython tuning: 3.715394917589437e-05 [##########] 100.00% Done...

Experiment saved to USER_res.pkl
<spotpython.spot.spot.Spot at 0x152a54550>

23.4 Results

_ = spot_user.print_results()
min y: 3.715394917589437e-05
User Pressure: 0.05170658955305796
User Temp: 0.07401195908206382
spot_user.plot_progress()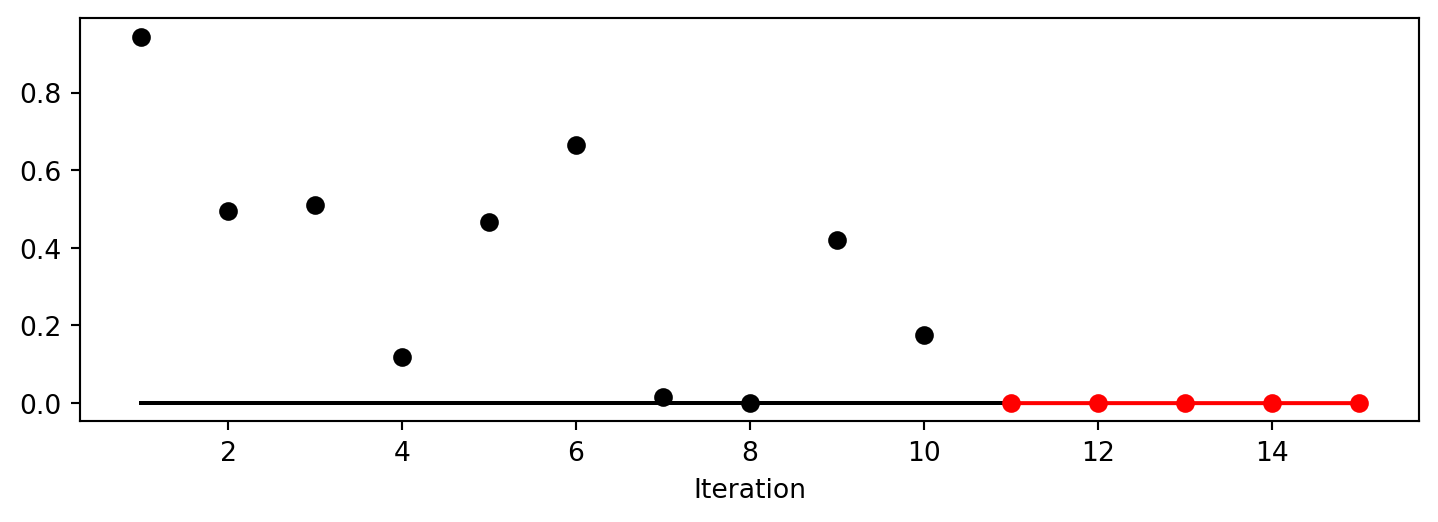

23.5 A Contour Plot

We can select two dimensions, say \(i=0\) and \(j=1\), and generate a contour plot as follows.

NoteNote:

We have specified identical min_z and max_z values to generate comparable plots.

spot_user.plot_contour(i=0, j=1, min_z=0, max_z=2.25)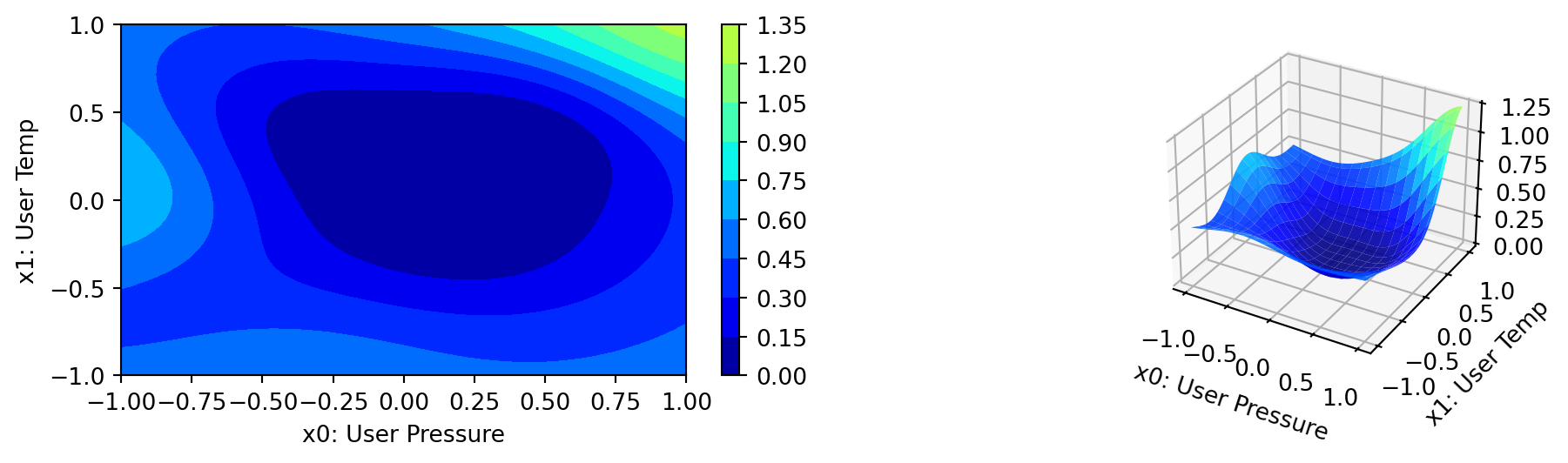

  • The variable importance:
_ = spot_user.print_importance()
User Pressure:  59.77997388560076
User Temp:  100.0
spot_user.plot_importance()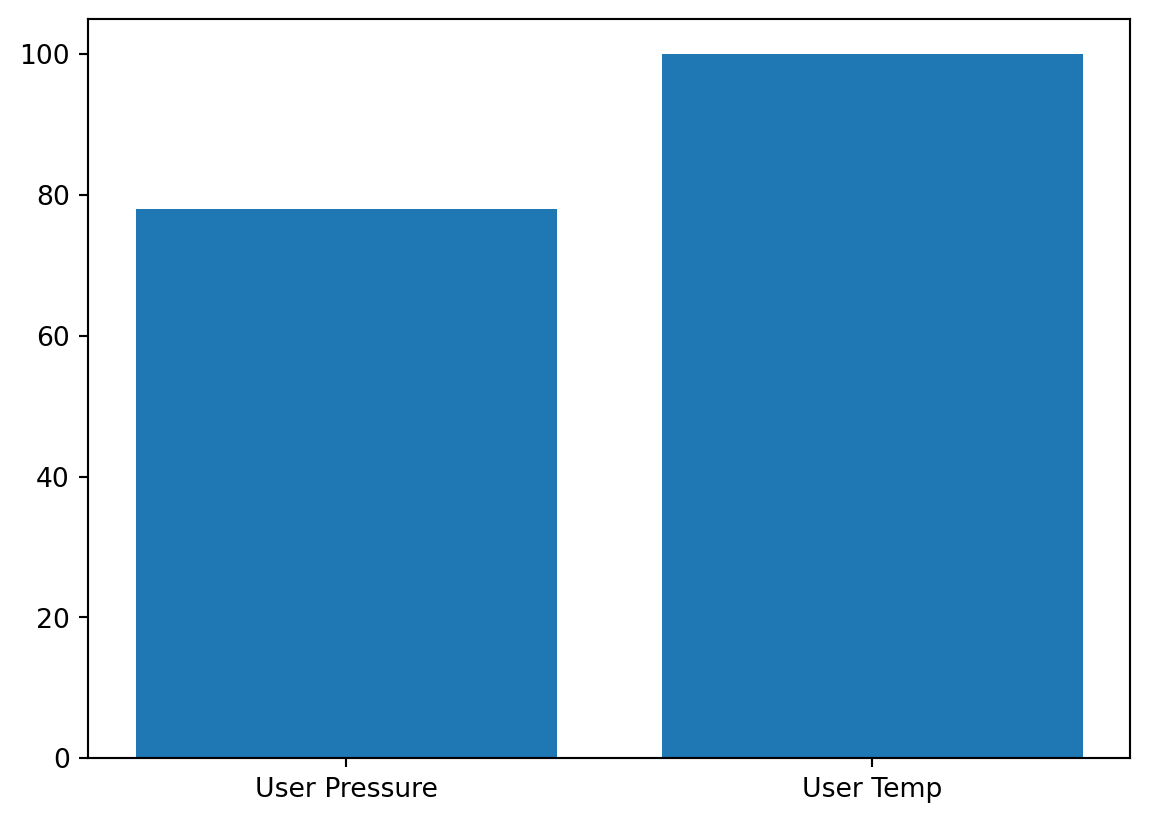

23.6 Multi-Objective Functions

  • The spotpython package can also handle multi-objective functions, which are functions that return multiple values for each input vector.
  • As noted in Section 23.2, in the single-objective case, the function returns one value for each input vector and spotpython expects a 1D array as output.
  • If the function returns a 2D array as output, spotpython will treat it as a multi-objective function result.

23.6.1 Response Surface Experiment

Myers, Montgomery, and Anderson-Cook (2016) describe a response surface experiment where three input variables (reaction time, reaction temperature, and percent catalyst) were used to model two characteristics of a chemical reaction: percent conversion and thermal activity. Their model is based on the following equations:

\[\begin{align*} f_{\text{con}}(x) = & 81.09 + 1.0284 \cdot x_1 + 4.043 \cdot x_2 + 6.2037 \cdot x_3 + 1.8366 \cdot x_1^2 + 2.9382 \cdot x_2^2 \\ & + 5.1915 \cdot x_3^2 + 2.2150 \cdot x_1 \cdot x_2 + 11.375 \cdot x_1 \cdot x_3 + 3.875 \cdot x_2 \cdot x_3 \end{align*}\] and \[\begin{align*} f_{\text{act}}(x) = & 59.85 + 3.583 \cdot x_1 + 0.2546 \cdot x_2 + 2.2298 \cdot x_3 + 0.83479 \cdot x_1^2 + 0.07484 \cdot x_2^2 \\ & + 0.05716 \cdot x_3^2 + 0.3875 \cdot x_1 \cdot x_2 + 0.375 \cdot x_1 \cdot x_3 + 0.3125 \cdot x_2 \cdot x_3. \end{align*}\]

23.6.1.1 Defining the Multi-Objective Function myer16a

  • The multi-objective function myer16a combines the results of two single-objective functions: conversion and activity.
  • It is implemented in spotpython as follows:
import numpy as np

def conversion_pred(X):
    """
    Compute conversion predictions for each row in the input array.

    Args:
        X (np.ndarray): 2D array where each row is a configuration.

    Returns:
        np.ndarray: 1D array of conversion predictions.
    """
    return (
        81.09
        + 1.0284 * X[:, 0]
        + 4.043 * X[:, 1]
        + 6.2037 * X[:, 2]
        - 1.8366 * X[:, 0]**2
        + 2.9382 * X[:, 1]**2
        - 5.1915 * X[:, 2]**2
        + 2.2150 * X[:, 0] * X[:, 1]
        + 11.375 * X[:, 0] * X[:, 2]
        - 3.875 * X[:, 1] * X[:, 2]
    )

def activity_pred(X):
    """
    Compute activity predictions for each row in the input array.

    Args:
        X (np.ndarray): 2D array where each row is a configuration.

    Returns:
        np.ndarray: 1D array of activity predictions.
    """
    return (
        59.85
        + 3.583 * X[:, 0]
        + 0.2546 * X[:, 1]
        + 2.2298 * X[:, 2]
        + 0.83479 * X[:, 0]**2
        + 0.07484 * X[:, 1]**2
        + 0.05716 * X[:, 2]**2
        - 0.3875 * X[:, 0] * X[:, 1]
        - 0.375 * X[:, 0] * X[:, 2]
        + 0.3125 * X[:, 1] * X[:, 2]
    )

def fun_myer16a(X, fun_control=None):
    """
    Compute both conversion and activity predictions for each row in the input array.

    Args:
        X (np.ndarray): 2D array where each row is a configuration.
        fun_control (dict, optional): Additional control parameters (not used here).

    Returns:
        np.ndarray: 2D array where each row contains [conversion_pred, activity_pred].
    """
    return np.column_stack((conversion_pred(X), activity_pred(X)))

Now the function returns a 2D array with two columns, one for each objective function. The first column corresponds to the conversion prediction, and the second column corresponds to the activity prediction.

X = np.array([[1, 2, 3], [4, 5, 6]])
results = fun_myer16a(X)
print(results)
[[ 87.3132   72.25519]
 [200.8662   98.7442 ]]

23.6.1.2 Using a Weighted Sum

  • The spotpython package can also handle multi-objective functions, which are functions that return multiple values for each input vector.
  • In this case, we can use a weighted sum to combine the two objectives into a single objective function.
  • The function aggergate takes the two objectives and combines them into a single objective function by applying weights to each objective.
  • The weights can be adjusted to give more importance to one objective over the other.
  • For example, if we want to give more importance to the conversion prediction, we can set the weight for the conversion prediction to 2 and the weight for the activity prediction to 0.1.
# Weight first objective with 2, second with 1/10
def aggregate(y):
    return np.sum(y*np.array([2, 0.1]), axis=1)

The aggregate function object is passed to the fun_control dictionary aas the fun_mo2so argument.

fun_control = fun_control_init(
              lower = np.array( [0, 0, 0]),
              upper = np.array([1, 1, 1]),
              fun_mo2so=aggregate)
S = Spot(fun=fun_myer16a,
        fun_control=fun_control)
S.run()
S.plot_progress()
Anisotropic model: n_theta set to 3
Anisotropic model: n_theta set to 3
spotpython tuning: 171.6572030008439 [#######---] 73.33% 
Anisotropic model: n_theta set to 3
spotpython tuning: 168.32536280172403 [########--] 80.00% 
Anisotropic model: n_theta set to 3
spotpython tuning: 168.26312173119723 [#########-] 86.67% 
Anisotropic model: n_theta set to 3
spotpython tuning: 168.16500000000002 [#########-] 93.33% 
Anisotropic model: n_theta set to 3
spotpython tuning: 168.16500000000002 [##########] 100.00% Done...

Experiment saved to 000_res.pkl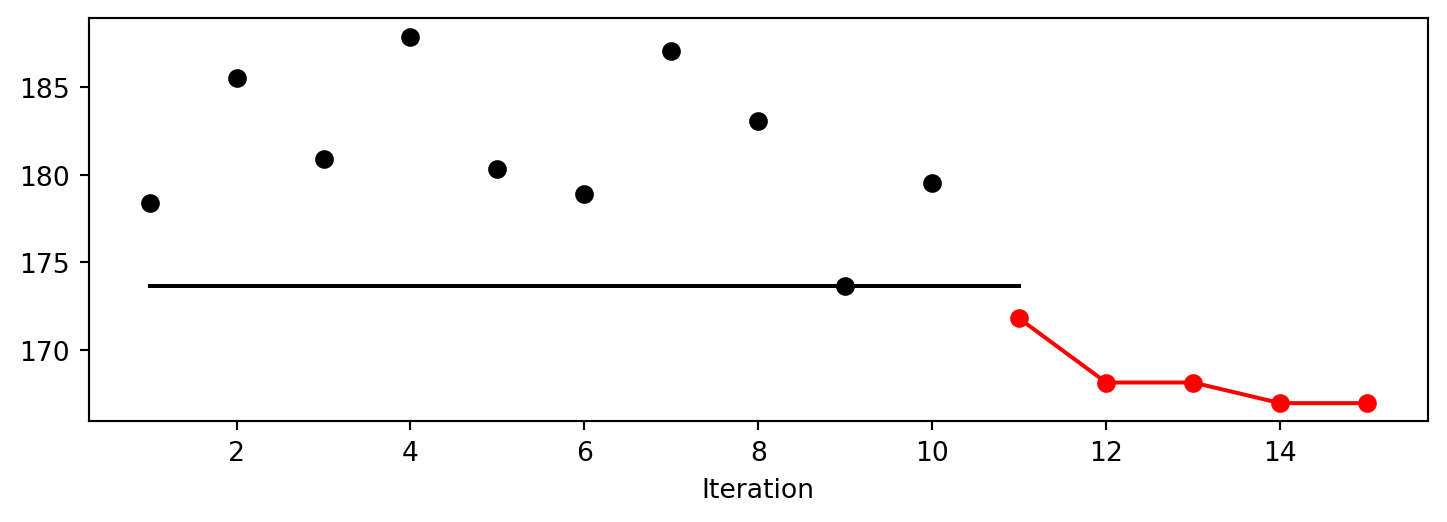

If no fun_mo2so function is specified, the spotpython package will use the first return value of the multi-objective function as the single objective function.

spotpython allows access to the complete history of multi-objective return values. They are stored in the y_mo attribute of the Spot object. The y_mo attribute is a 2D array where each row corresponds to a configuration and each column corresponds to an objective function. These values can be visualized as shown in Figure 23.1.

y_mo = S.y_mo
y = S.y
plt.xlim(0, len(y_mo))
plt.ylim(0.9 * np.min(y_mo), 1.1* np.max(y))
plt.scatter(range(len(y_mo)), y_mo[:, 0], label='Conversion', marker='o')
plt.scatter(range(len(y_mo)), y_mo[:, 1], label='Activity', marker='x')
plt.plot(np.minimum.accumulate(y_mo[:, 0]), label='Cum. Min Conversion')
plt.plot(np.minimum.accumulate(y_mo[:, 1]), label='Cum. Min Activity')
plt.scatter(range(len(y)), y, label='Agg. Result', marker='D', color='red')
plt.plot(np.minimum.accumulate(y), label='Cum. Min Agg. Res.', color='red')
plt.xlabel('Iteration')
plt.ylabel('Objective Function Value')
plt.grid()
plt.title('Single- and Multi-Obj. Function Values')
plt.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.tight_layout()
plt.show()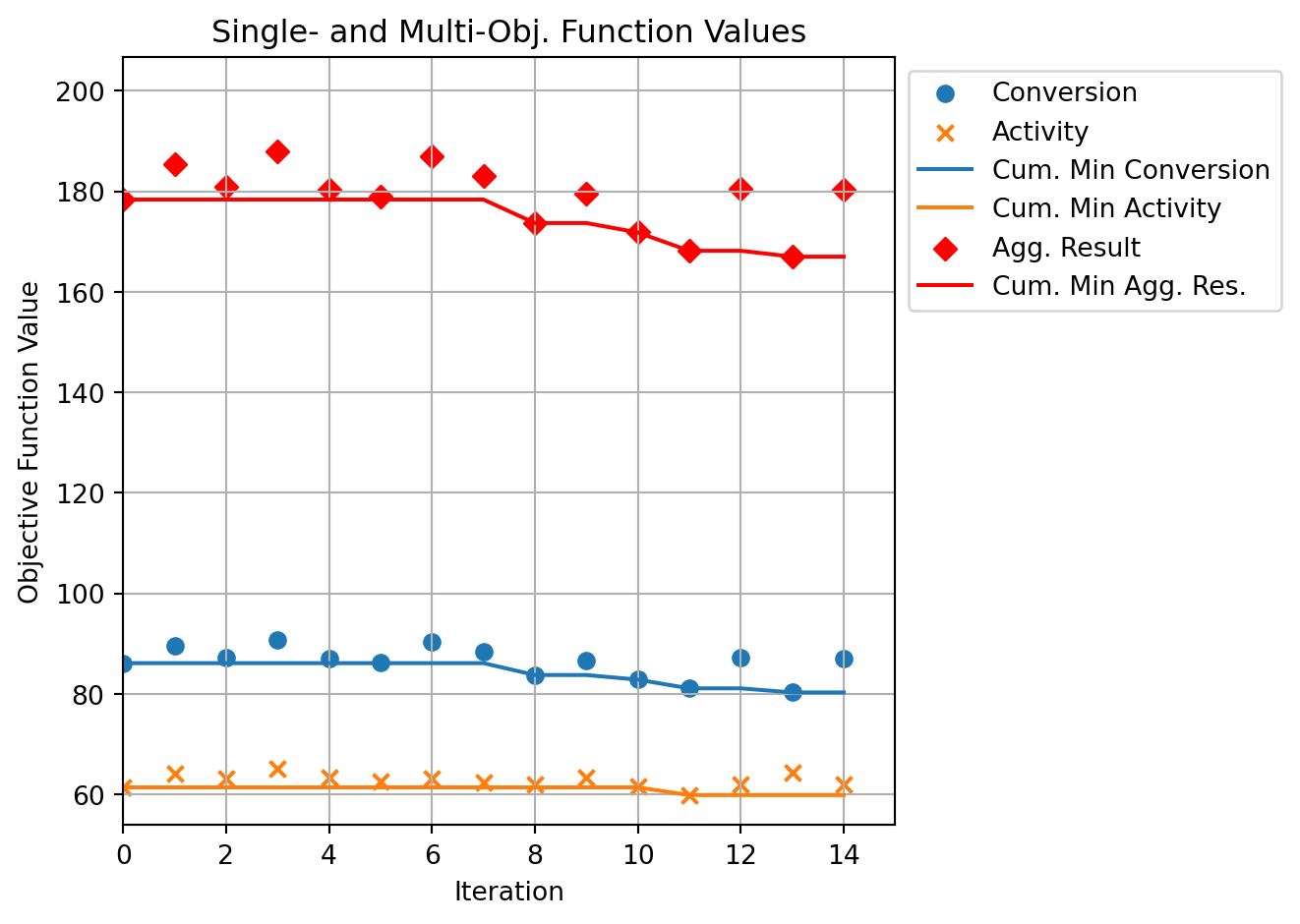
Figure 23.1: Single- and Multi-Objective Function Values. The red line shows the optimization progress based on the aggregated objective function. The blue lines show the progress of the conversion objective, the orange line the progress of the activity objective. Points denote individual evaluations, lines the cumulative minimum of the respective objective function.

Since all values from the multi-objective functions can be accessed, more sophisticated multi-objective optimization methods can be implemented. For example, the spotpython package provides a pareto_front function that can be used to compute the Pareto front of the multi-objective function values, see pareto. The Pareto front is a set of solutions that are not dominated by any other solution in the objective space.

NoteSummary: Using spotpython with Multi-Objective User-Specified Functions
  • spotpython accepts user-specified multi-objective functions that can be defined in Python.
  • The function should accept a 2D array as input and return a 2D array as output.
  • An aggregate function can be used to combine multiple objectives into a single objective function.

23.7 Jupyter Notebook

Note