34  Hyperparameter Tuning with PyTorch Lightning: ResNets

Neural ODEs are related to Residual Neural Networks (ResNets). We consider ResNets in Section 34.1.

34.1 Residual Neural Networks

He et al. (2015) introduced Residual Neural Networks (ResNets).

34.1.1 Residual Connections

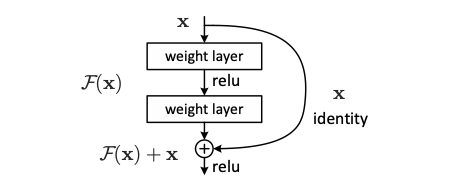
Residual connections are a key component of ResNets. They are used to stabilize the training of very deep networks. The idea is to learn a residual mapping instead of the full mapping. The residual mapping is defined as:

Definition 34.1 (Residual Connection) Let \(F\) denote a non-linear mapping (usually a sequence of NN modules likes convolutions, activation functions, and normalizations).

Instead of modeling \[ x_{l+1}=F(x_{l}), \] residual connections model \[ x_{l+1}=x_{l}+F(x_{l}). \tag{34.1}\]

This is illustrated in Figure 34.1.

Figure 34.1: Residual Connection. Figure credit He et al. (2015)

Applying backpropagation to the residual mapping results in the following gradient calculation:

\[ \frac{\partial x_{l+1}}{\partial x_{l}} = \mathbf{I} + \frac{\partial F(x_{l})}{\partial x_{l}}, \tag{34.2}\]

where \(\mathbf{I}\) is the identity matrix. The identity matrix is added to the gradient, which helps to stabilize the training of very deep networks. The identity matrix ensures that the gradient is not too small, which can happen if the gradient of \(F\) is close to zero. This is especially important for very deep networks, where the gradient can vanish quickly.

The bias towards the identity matrix guarantees a stable gradient propagation being less effected by \(F\) itself.

There have been many variants of ResNet proposed, which mostly concern the function \(F\), or operations applied on the sum. Figure 34.2 shows two different ResNet blocks:

• the original ResNet block, which applies a non-linear activation function, usually ReLU, after the skip connection. and
• the pre-activation ResNet block, which applies the non-linearity at the beginning of \(F\).

Figure 34.2: ResNet Block. Left: original Residual block in He et al. (2015). Right: pre-activation block. BN describes batch-normalization. Figure credit He et al. (2016)

For very deep network the pre-activation ResNet has shown to perform better as the gradient flow is guaranteed to have the identity matrix as shown in Equation 34.2, and is not harmed by any non-linear activation applied to it.

34.1.2 Implementation of the Original ResNet Block

One special case we have to handle is when we want to reduce the image dimensions in terms of width and height. The basic ResNet block requires \(F(x_{l})\) to be of the same shape as \(x_{l}\). Thus, we need to change the dimensionality of \(x_{l}\) as well before adding to \(F(x_{l})\). The original implementation used an identity mapping with stride 2 and padded additional feature dimensions with 0. However, the more common implementation is to use a 1x1 convolution with stride 2 as it allows us to change the feature dimensionality while being efficient in parameter and computation cost. The code for the ResNet block is relatively simple, and shown below:

import torch
import torch.nn as nn

class ResNetBlock(nn.Module):
    def __init__(self, c_in, act_fn, subsample=False, c_out=-1):
        """
        Inputs:
            c_in - Number of input features
            act_fn - Activation class constructor (e.g. nn.ReLU)
            subsample - If True, we need to apply a transformation inside the block to change the feature dimensionality
            c_out - Number of output features. Note that this is only relevant if subsample is True, as otherwise, c_out = c_in
        """
        super().__init__()
        if not subsample:
            c_out = c_in

        # Network representing F
        self.net = nn.Sequential(
            nn.Linear(c_in, c_out, bias=False),  # Linear layer for feature transformation
            nn.BatchNorm1d(c_out),               # Batch normalization for stable learning
            act_fn(),                            # Activation function
            nn.Linear(c_out, c_out, bias=False), # Second linear layer
            nn.BatchNorm1d(c_out)                # Batch normalization
        )
        
        # If subsampling, adjust the input feature dimensionality using a linear layer
        self.downsample = nn.Linear(c_in, c_out) if subsample else None
        self.act_fn = act_fn()

    def forward(self, x):
        z = self.net(x)  # Apply the main network
        if self.downsample is not None:
            x = self.downsample(x)  # Adjust dimensionality if necessary
        out = z + x  # Residual connection
        out = self.act_fn(out)  # Apply activation function
        return out

class ResNetRegression(nn.Module):
    def __init__(self, input_dim, output_dim, block, num_blocks=1, hidden_dim=64, act_fn=nn.ReLU):
        super().__init__()
        self.input_layer = nn.Linear(input_dim, hidden_dim)  # Input layer transformation
        self.blocks = nn.ModuleList([block(hidden_dim, act_fn) for _ in range(num_blocks)])  # List of ResNet blocks
        self.output_layer = nn.Linear(hidden_dim, output_dim)  # Output layer for regression
        
    def forward(self, x):
        x = self.input_layer(x)  # Apply input layer
        for block in self.blocks:
            x = block(x)  # Apply each block
        x = self.output_layer(x)  # Get final output
        return x

input_dim = 10
output_dim = 1
hidden_dim = 64
model = ResNetRegression(input_dim, output_dim, ResNetBlock, num_blocks=2, hidden_dim=hidden_dim, act_fn=nn.ReLU)
model

ResNetRegression(
  (input_layer): Linear(in_features=10, out_features=64, bias=True)
  (blocks): ModuleList(
    (0-1): 2 x ResNetBlock(
      (net): Sequential(
        (0): Linear(in_features=64, out_features=64, bias=False)
        (1): BatchNorm1d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
        (2): ReLU()
        (3): Linear(in_features=64, out_features=64, bias=False)
        (4): BatchNorm1d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
      )
      (act_fn): ReLU()
    )
  )
  (output_layer): Linear(in_features=64, out_features=1, bias=True)
)

# Create a sample input tensor with a batch size of 2
from torchviz import make_dot
sample_input = torch.randn(2, input_dim)

# Generate the visualization
output = model(sample_input)
dot = make_dot(output, params=dict(model.named_parameters()))

# Save and render the visualization
dot.format = 'png'
dot.render('./figures_static/resnet_regression')

'figures_static/resnet_regression.png'

ResNet Regression

34.1.3 Implementation of the Pre-Activation ResNet Block

The second block we implement is the pre-activation ResNet block. For this, we have to change the order of layer in self.net, and do not apply an activation function on the output. Additionally, the downsampling operation has to apply a non-linearity as well as the input, \(x_l\), has not been processed by a non-linearity yet. Hence, the block looks as follows:

import torch
import torch.nn as nn

class PreActResNetBlock(nn.Module):
    def __init__(self, c_in, act_fn, subsample=False, c_out=-1):
        super().__init__()
        if not subsample:
            c_out = c_in
        self.net = nn.Sequential(
            nn.LayerNorm(c_in),  # Replacing BatchNorm1d with LayerNorm
            act_fn(),
            nn.Linear(c_in, c_out, bias=False),
            nn.LayerNorm(c_out),
            act_fn(),
            nn.Linear(c_out, c_out, bias=False)
        )
        self.downsample = nn.Sequential(
            nn.LayerNorm(c_in),
            act_fn(),
            nn.Linear(c_in, c_out, bias=False)
        ) if subsample else None

    def forward(self, x):
        z = self.net(x)
        if self.downsample is not None:
            x = self.downsample(x)
        out = z + x
        return out

class PreActResNetRegression(nn.Module):
    def __init__(self, input_dim, output_dim, block, num_blocks=1, hidden_dim=64, act_fn=nn.ReLU):
        super().__init__()
        self.input_layer = nn.Linear(input_dim, hidden_dim)
        self.blocks = nn.ModuleList([block(hidden_dim, act_fn) for _ in range(num_blocks)])
        self.output_layer = nn.Linear(hidden_dim, output_dim)
        
    def forward(self, x):
        x = self.input_layer(x)
        for block in self.blocks:
            x = block(x)
        x = self.output_layer(x)
        return x

input_dim = 10
output_dim = 1
hidden_dim = 64
model = PreActResNetRegression(input_dim, output_dim, PreActResNetBlock, num_blocks=2, hidden_dim=hidden_dim, act_fn=nn.ReLU)
model

PreActResNetRegression(
  (input_layer): Linear(in_features=10, out_features=64, bias=True)
  (blocks): ModuleList(
    (0-1): 2 x PreActResNetBlock(
      (net): Sequential(
        (0): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
        (1): ReLU()
        (2): Linear(in_features=64, out_features=64, bias=False)
        (3): LayerNorm((64,), eps=1e-05, elementwise_affine=True)
        (4): ReLU()
        (5): Linear(in_features=64, out_features=64, bias=False)
      )
    )
  )
  (output_layer): Linear(in_features=64, out_features=1, bias=True)
)

from torchviz import make_dot
# Create a sample input tensor
sample_input = torch.randn(1, input_dim)

# Generate the visualization
output = model(sample_input)
dot = make_dot(output, params=dict(model.named_parameters()))

# Save and render the visualization
dot.format = 'png'
dot.render('./figures_static/preact_resnet_regression')

'figures_static/preact_resnet_regression.png'

Pre-Activation ResNet Regression

34.1.4 The Overall ResNet Architecture

The overall ResNet architecture for regression consists of stacking multiple ResNet blocks, of which some are downsampling the input. When discussing ResNet blocks within the entire network, they are usually grouped by output shape. If we describe the ResNet as having [3,3,3] blocks, it means there are three groups of ResNet blocks, each containing three blocks, with downsampling occurring in the first block of the second and third groups. The final layer produces continuous outputs suitable for regression tasks.

ResNet Notation. Figure credit Lippe (2022)

The output_dim parameter is used to determine the number of outputs for regression. This is set to 1 for a single regression target by default, but can be adjusted for multiple targets. Note, a final layer without a softmax or similar classification layer has to be added for regression tasks. A similar notation is used by many other implementations such as in the torchvision library from PyTorch.

Example 34.1 (Example ResNet Model)  

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import make_regression
from types import SimpleNamespace

def get_resnet_blocks_by_name():
    return {"ResNetBlock": ResNetBlock}

def get_act_fn_by_name():
    return {"relu": nn.ReLU}

# Define a simple ResNetBlock for fully connected layers
class ResNetBlock(nn.Module):
    def __init__(self, c_in, act_fn, subsample=False, c_out=-1):
        super().__init__()
        if not subsample:
            c_out = c_in

        self.net = nn.Sequential(
            nn.Linear(c_in, c_out, bias=False),
            nn.BatchNorm1d(c_out),
            act_fn(),
            nn.Linear(c_out, c_out, bias=False),
            nn.BatchNorm1d(c_out)
        )
        
        self.downsample = nn.Linear(c_in, c_out) if subsample else None
        self.act_fn = act_fn()

    def forward(self, x):
        z = self.net(x)
        if self.downsample is not None:
            x = self.downsample(x)
        out = z + x
        out = self.act_fn(out)
        return out

# Generate a simple random dataset for regression
num_samples = 100
num_features = 20  # Number of features, typical in a regression dataset
X, y = make_regression(n_samples=num_samples, n_features=num_features, noise=0.1)

# Convert to PyTorch tensors
X_tensor = torch.tensor(X, dtype=torch.float32)
y_tensor = torch.tensor(y, dtype=torch.float32).unsqueeze(1)  # Add a dimension for compatibility

# Define the ResNet model for regression
class ResNet(nn.Module):
    def __init__(self, input_dim, output_dim, num_blocks=[3, 3, 3], c_hidden=[64, 64, 64], act_fn_name="relu", block_name="ResNetBlock", **kwargs):
        super().__init__()
        resnet_blocks_by_name = get_resnet_blocks_by_name()
        act_fn_by_name = get_act_fn_by_name()
        assert block_name in resnet_blocks_by_name
        self.hparams = SimpleNamespace(output_dim=output_dim, 
                                       c_hidden=c_hidden, 
                                       num_blocks=num_blocks, 
                                       act_fn_name=act_fn_name,
                                       act_fn=act_fn_by_name[act_fn_name],
                                       block_class=resnet_blocks_by_name[block_name])
        self._create_network(input_dim)
        self._init_params()

    def _create_network(self, input_dim):
        c_hidden = self.hparams.c_hidden
        self.input_net = nn.Sequential(
            nn.Linear(input_dim, c_hidden[0]),
            self.hparams.act_fn()
        )

        blocks = []
        for block_idx, block_count in enumerate(self.hparams.num_blocks):
            for bc in range(block_count):
                subsample = (bc == 0 and block_idx > 0)
                blocks.append(
                    self.hparams.block_class(c_in=c_hidden[block_idx if not subsample else block_idx-1],
                                             act_fn=self.hparams.act_fn,
                                             subsample=subsample,
                                             c_out=c_hidden[block_idx])
                )
        self.blocks = nn.Sequential(*blocks)

        self.output_net = nn.Linear(c_hidden[-1], self.hparams.output_dim)

    def _init_params(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
            elif isinstance(m, nn.BatchNorm1d):
                nn.init.constant_(m.weight, 1)
                nn.init.constant_(m.bias, 0)

    def forward(self, x):
        x = self.input_net(x)
        x = self.blocks(x)
        x = self.output_net(x)
        return x

# Instantiate the model
model = ResNet(input_dim=num_features, output_dim=1)

# Define a loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=1e-3)

# Example training loop
num_epochs = 10
for epoch in range(num_epochs):
    model.train()
    optimizer.zero_grad()
    
    # Forward pass
    output = model(X_tensor)
    
    # Compute loss
    loss = criterion(output, y_tensor)
    
    # Backward pass and optimization
    loss.backward()
    optimizer.step()
    
    print(f'Epoch {epoch+1}/{num_epochs}, Loss: {loss.item()}')

Epoch 1/10, Loss: 49785.9609375
Epoch 2/10, Loss: 45109.39453125
Epoch 3/10, Loss: 41803.6640625
Epoch 4/10, Loss: 39092.62109375
Epoch 5/10, Loss: 36718.65625
Epoch 6/10, Loss: 34557.96484375
Epoch 7/10, Loss: 32503.44921875
Epoch 8/10, Loss: 30585.46484375
Epoch 9/10, Loss: 28826.705078125
Epoch 10/10, Loss: 27082.369140625

He, Kaiming, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. 2015. “Deep Residual Learning for Image Recognition.”

———. 2016. “Identity Mappings in Deep Residual Networks.” arXiv e-Prints, March, arXiv:1603.05027.

Lippe, Phillip. 2022. “UvA Deep Learning Tutorials.” https://github.com/phlippe/uvadlc_notebooks/tree/master.