import numpy as np
from scipy.spatial.distance import pdist, squareform, cdist
from numpy.linalg import cholesky, solve, LinAlgError
from numpy import spacing, sqrt, exp, multiply, eye, ones
from scipy.optimize import minimize
from scipy.stats import qmc
import matplotlib.pyplot as plt
import numpy as np
import matplotlib.pyplot as plt
from numpy import (exp, multiply, eye, linspace, spacing, sqrt)
from numpy.linalg import cholesky, solve
from scipy.spatial.distance import squareform, pdist, cdist
from scipy.optimize import minimize # Für die Optimierung
# 1. Definition der KrigingRegressor-Klasse
class KrigingRegressor:
"""Ein Kriging-Regressionsmodell mit Hyperparameter-Optimierung.
Attributes:
initial_theta (float): Startwert für den Aktivitätsparameter Theta.
bounds (list): Liste von Tupeln für die Grenzen der Hyperparameter-Optimierung.
opt_theta_ (float): Optimierter Theta-Wert nach dem Fitting.
X_train_ (array): Trainings-Eingabedaten.
y_train_ (array): Trainings-Zielwerte.
U_ (array): Cholesky-Zerlegung der Korrelationsmatrix.
mu_hat_ (float): Geschätzter Mittelwert.
"""
def __init__(self, initial_theta=1.0, bounds=[(0.001, 100.0)]):
self.initial_theta = initial_theta
self.bounds = bounds
def _build_Psi(self, X, log_theta, eps=sqrt(spacing(1))):
"""Berechnet die Korrelationsmatrix Psi.
Args:
X (np.ndarray): Eingabedaten-Matrix
log_theta (float or np.ndarray): Log10-transformierte Theta-Werte
eps (float, optional): Nugget-Term für numerische Stabilität
Returns:
np.ndarray: Korrelationsmatrix Psi
"""
# Konvertiere log_theta zurück zu theta (immer positiv durch exp)
theta = 10.0**log_theta
if not isinstance(theta, np.ndarray) or theta.ndim == 0:
theta = np.array([theta])
D = squareform(pdist(X, metric='sqeuclidean', w=theta))
Psi = exp(-D)
Psi += multiply(eye(X.shape[0]), eps)
return Psi
def _build_psi(self, X_train, x_predict, log_theta):
"""Berechnet den Korrelationsvektor psi.
Args:
X_train (np.ndarray): Trainings-Eingabedaten
x_predict (np.ndarray): Vorhersage-Eingabepunkte
log_theta (float or np.ndarray): Log10-transformierte Theta-Werte
Returns:
np.ndarray: Korrelationsvektor psi
"""
# Konvertiere log_theta zurück zu theta
theta = 10.0**log_theta
if not isinstance(theta, np.ndarray) or theta.ndim == 0:
theta = np.array([theta])
D = cdist(x_predict, X_train, metric='sqeuclidean', w=theta)
psi = exp(-D)
return psi.T
def _neg_log_likelihood(self, params, X_train, y_train):
"""Berechnet die negative konzentrierte Log-Likelihood."""
theta = params
n = X_train.shape[0]
try:
Psi = self._build_Psi(X_train, theta)
U = cholesky(Psi).T
except np.linalg.LinAlgError:
return 1e15
one = np.ones(n).reshape(-1, 1)
# Berechne mu_hat (MLE des Mittelwerts)
Psi_inv_y = solve(U, solve(U.T, y_train))
Psi_inv_one = solve(U, solve(U.T, one))
mu_hat = (one.T @ Psi_inv_y) / (one.T @ Psi_inv_one)
mu_hat = mu_hat.item()
# Berechne sigma_hat_sq (MLE der Prozessvarianz)
y_minus_mu_one = y_train - one * mu_hat
sigma_hat_sq = (y_minus_mu_one.T @ Psi_inv_y) / n
sigma_hat_sq = sigma_hat_sq.item()
if sigma_hat_sq < 1e-10:
return 1e15
# Berechne negative konzentrierte Log-Likelihood
log_det_Psi = 2 * np.sum(np.log(np.diag(U.T)))
nll = 0.5 * (n * np.log(sigma_hat_sq) + log_det_Psi)
return nll
def fit(self, X, y):
"""Fit das Kriging-Modell an die Trainingsdaten.
Args:
X (array-like): Eingabedaten der Form (n_samples, n_features)
y (array-like): Zielwerte der Form (n_samples,)
Returns:
self: Das gefittete Kriging-Modell
Notes:
Diese Methode optimiert die Hyperparameter Theta, indem sie die negative Log-Likelihood minimiert.
"""
self.X_train_ = X
self.y_train_ = y.reshape(-1, 1)
# Optimierung der Hyperparameter
initial_theta = np.array([self.initial_theta])
result = minimize(self._neg_log_likelihood,
initial_theta,
args=(self.X_train_, self.y_train_),
method='L-BFGS-B',
bounds=self.bounds)
self.opt_theta_ = result.x
# Berechne optimale Parameter für Vorhersagen
Psi_opt = self._build_Psi(self.X_train_, self.opt_theta_)
self.U_ = cholesky(Psi_opt).T
n_train = self.X_train_.shape[0]
one = np.ones(n_train).reshape(-1, 1)
self.mu_hat_ = (one.T @ solve(self.U_, solve(self.U_.T, self.y_train_))) / \
(one.T @ solve(self.U_, solve(self.U_.T, one)))
self.mu_hat_ = self.mu_hat_.item()
return self
def predict(self, X):
"""Vorhersage für neue Datenpunkte.
Args:
X (array-like): Eingabedaten für Vorhersage der Form (n_samples, n_features)
Returns:
array: Vorhergesagte Werte
"""
n_train = self.X_train_.shape[0]
one = np.ones(n_train).reshape(-1, 1)
# Fix: Use self._build_psi instead of build_psi
psi = self._build_psi(self.X_train_, X, self.opt_theta_)
return self.mu_hat_ * np.ones(X.shape[0]).reshape(-1, 1) + \
psi.T @ solve(self.U_, solve(self.U_.T,
self.y_train_ - one * self.mu_hat_))68 Lernmodul: Kriging Projekt
Um die gestellte Aufgabe zu lösen, erstellen wir eine Python-Klasse KrigingRegressor für das Kriging-Modell, eine Black-Box-Funktion f(x), eine Funktion zur Erstellung des initialen Stichprobenplans und implementieren dann den sequenziellen Optimierungsablauf.
1. Die KrigingRegressor-Klasse Diese Klasse kapselt die Logik für das Kriging-Modell, einschließlich der Berechnung der Korrelationsmatrizen, der Maximum-Likelihood-Schätzung für den globalen Mittelwert \(\hat{\mu}\) und die Prozessvarianz \(\hat{\sigma}^2\), der konzentrierten Log-Likelihood-Funktion zur Hyperparameter-Optimierung sowie der Vorhersagefunktion. Die Optimierung des Aktivitätsparameters \(\vec{\theta}\) erfolgt über die Maximierung der konzentrierten Log-Likelihood-Funktion, wobei intern die negative Log-Likelihood minimiert wird. Der Glattheitsparameter \(\vec{p}\) wird implizit auf \(p_j=2\) gesetzt, da die quadrierte euklidische Distanz verwendet wird. Es wird ein kleiner Nugget-Term (eps) zur Diagonalen der Korrelationsmatrix hinzugefügt, um die numerische Stabilität zu gewährleisten.
2. Die Black-Box-Funktion f(x) Diese Funktion simuliert ein teures oder undurchsichtiges System, dessen interne Funktionsweise dem Optimierungsalgorithmus nicht bekannt ist. Im weiteren Schritt wird ein Server zur Beantwortung der Auswertungen bereitgestellt, der die Black-Box-Funktion ausführt. In diesem Beispiel verwenden wir eine analytische Funktion, die eine gewisse Komplexität aufweist, um die Black-Box zu simulieren.
3. Initialer Stichprobenplan X Für einen “optimalen” Versuchsplan wird Latin Hypercube Sampling (LHS) verwendet, da dies eine raumfüllende Eigenschaft aufweist. Dies stellt sicher, dass der Eingaberaum effizient erkundet wird. Die Eingabedaten werden intern auf den Bereich $$ skaliert, um die Konsistenz der \(\theta\)-Werte über verschiedene Probleme hinweg zu gewährleisten.
4. Sequenzieller Optimierungsablauf Der Prozess beginnt mit einem initialen Stichprobenplan. In jeder Iteration wird das Kriging-Modell mit den verfügbaren Daten gefittet. Anschließend wird eine Optimierung auf dem Surrogatmodell (dem gefitteten Kriging-Modell) durchgeführt, um den nächsten vielversprechenden Punkt im Designraum zu finden. Dieser Punkt wird der Black-Box-Funktion übergeben, und die erhaltene Beobachtung wird zum Trainingsdatensatz hinzugefügt. Dieser iterative Prozess wird bis zu einer maximalen Anzahl von Funktionsauswertungen fortgesetzt.
Hier ist der entsprechende Python-Code:
69 2. Die Black-Box-Funktion
def f_black_box(x):
"""Analytische Black-Box-Funktion: f(x)"""
return -x**2*np.cos(x) + 1 + x**2*np.sin(x)# 3. Funktion zur Erstellung des initialen Stichprobenplans (Latin Hypercube Sampling)
def create_initial_design(n_points, dimensionality, x_range):
"""Erstellt einen raumfüllenden initialen Versuchsplan mittels Latin Hypercube Sampling.
Args:
n_points (int): Anzahl der Designpunkte
dimensionality (int): Dimension des Eingaberaums
x_range (tuple): Tuple mit (unterer_grenze, oberer_grenze) für den Wertebereich
Returns:
np.ndarray: Matrix der Designpunkte der Form (n_points, dimensionality)
"""
# Verwende einen Integer als Seed statt SeedSequence
sampler = qmc.LatinHypercube(d=dimensionality, seed=1234)
# Generiere Samples im Einheitswürfel [0,1]^d
lhs_samples_unit_cube = sampler.random(n=n_points)
# Extrahiere die Grenzen
x_lower, x_upper = x_range
# Skaliere die Samples vom Einheitswürfel auf den gewünschten Bereich
X_initial = x_lower + (x_upper - x_lower) * lhs_samples_unit_cube
# Stelle sicher, dass das Output ein 2D Array ist
return X_initial.reshape(-1, dimensionality)70 Hauptskript für die sequentielle Optimierung
np.random.seed(42) # Für Reproduzierbarkeit der Zufallszahlen
# Definition des Suchraums für die Black-Box-Funktion
x_lower_bound = -5.0
x_upper_bound = 5.0
search_range = (x_lower_bound, x_upper_bound)
dimensionality = 1 # f(x) = x^2 + 1 ist 1-dimensional
# Parameter für den initialen Stichprobenplan
n_initial_points = 7
# Maximale Gesamtzahl an Funktionsauswertungen
N_max_evaluations = 20
# --- Schritt 1: Initialen Stichprobenplan erstellen und Black-Box-Funktion auswerten ---
X_train_current = create_initial_design(n_initial_points, dimensionality, search_range)
y_train_current = f_black_box(X_train_current)
print(f"Initialer X_train (n={n_initial_points}):\n{np.round(X_train_current.flatten(), 3)}")
print(f"Zugehöriger y_train:\n{np.round(y_train_current.flatten(), 3)}")
print("-" * 70)Initialer X_train (n=7):
[-3.538 -4.115 -2.033 4.626 3.116 1.974 0.369]
Zugehöriger y_train:
[ 17.382 24.522 -0.856 -18.479 10.956 6.114 0.922]
----------------------------------------------------------------------# --- Schritt 2: KrigingRegressor-Modell initialisieren ---# Bounds für log10(theta), z.B. 10^-3 bis 10^2
theta_bounds_log10 = [(-3.0, 2.0)]
M_1 = KrigingRegressor(initial_theta=1.0, bounds=theta_bounds_log10)
# --- Schritt 3: Sequenzieller Optimierungs-Loop ---
# Anzahl der Punkte, die nach dem initialen Plan hinzugefügt werden
num_infill_steps = N_max_evaluations - n_initial_points
for i in range(num_infill_steps + 1): # +1, um auch nach dem letzten Infill-Punkt zu fitten
current_evals = len(X_train_current)
print(f"\n--- Iteration {i+1} (Gesamtauswertungen: {current_evals}) ---")
# Modell mit den aktuellen Daten fitten
print("Kriging-Modell wird gefittet...")
M_1.fit(X_train_current, y_train_current)
print(f"Optimiertes Theta: {np.round(M_1.opt_theta_.item(), 4)}")
print(f"Geschätzter globaler Mittelwert (mu_hat): {np.round(M_1.mu_hat_, 4)}")
# Überprüfen, ob die maximale Anzahl an Auswertungen erreicht wurde
if current_evals >= N_max_evaluations:
print("Maximale Anzahl an Auswertungen erreicht. Optimierung wird beendet.")
break
--- Iteration 1 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 2 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 3 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 4 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 5 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 6 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 7 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 8 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 9 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 10 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 11 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 12 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 13 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.5178
--- Iteration 14 (Gesamtauswertungen: 7) ---
Kriging-Modell wird gefittet...
Optimiertes Theta: -0.1013
Geschätzter globaler Mittelwert (mu_hat): 3.517871 — Schritt 4: Surrogat-basierte Optimierung zur Suche des nächsten Infill-Punktes —
Definiere die Zielfunktion für die innere Optimierung (Minimierung des Surrogats)
def surrogate_objective(x_val):
# Stelle sicher, dass x_val im richtigen Format (2D-Array) für predict ist
x_val_reshaped = np.atleast_2d(x_val)
return M_1.predict(x_val_reshaped).item() # Rückgabe als Skalar72 Suchgrenzen für die Optimierung auf dem Surrogatmodell
surrogate_search_bounds = [(x_lower_bound, x_upper_bound)] * dimensionality
print("Optimierung auf dem Surrogatmodell, um den nächsten Infill-Punkt zu finden...")
# Anfangsschätzung für die Surrogat-Optimierung (zufälliger Punkt im Suchraum)
x0_surrogate_opt = np.random.uniform(low=x_lower_bound, high=x_upper_bound, size=dimensionality)
# Verwende L-BFGS-B für die Surrogat-Optimierung
surrogate_opt_result = minimize(surrogate_objective,
x0=x0_surrogate_opt,
method='L-BFGS-B',
bounds=surrogate_search_bounds)
x_new_infill = np.atleast_2d(surrogate_opt_result.x) # Sicherstellen, dass 2D-Array
y_new_infill = f_black_box(x_new_infill) # Auswertung des neuen Punktes durch Black-Box
print(f"Neuer Infill-Punkt x_1: {np.round(x_new_infill.flatten(), 3)}, "
f"Zugehöriger y_1 (Black-Box): {np.round(y_new_infill.item(), 3)}")
# Neuen Punkt zum Trainingsdatensatz hinzufügen
X_train_current = np.vstack((X_train_current, x_new_infill))
y_train_current = np.vstack((y_train_current, y_new_infill))
print(f"Aktueller X_train (total {len(X_train_current)} Punkte):\n{np.round(X_train_current.flatten(), 3)}")
print(f"Aktueller y_train:\n{np.round(y_train_current.flatten(), 3)}")
print("-" * 70)
print("\n--- Optimierungsprozess abgeschlossen ---")Optimierung auf dem Surrogatmodell, um den nächsten Infill-Punkt zu finden...
Neuer Infill-Punkt x_1: [-1.93], Zugehöriger y_1 (Black-Box): -1.178
Aktueller X_train (total 8 Punkte):
[-3.538 -4.115 -2.033 4.626 3.116 1.974 0.369 -1.93 ]
Aktueller y_train:
[ 17.382 24.522 -0.856 -18.479 10.956 6.114 0.922 -1.178]
----------------------------------------------------------------------
--- Optimierungsprozess abgeschlossen ---73 Fitte das finale Modell mit allen verfügbaren N_max_evaluations Punkten
M_1.fit(X_train_current, y_train_current)
# Visualisierung der Ergebnisse
x_plot = np.linspace(x_lower_bound, x_upper_bound, 200).reshape(-1, 1)
y_predict_final = M_1.predict(x_plot)
y_true = f_black_box(x_plot)
plt.figure(figsize=(10, 6))
plt.plot(x_plot, y_true, 'k--', linewidth=2, label='Wahre Funktion: $f(x)$')
plt.plot(X_train_current, y_train_current, 'bo', markersize=8, label=f'Ausgewertete Punkte (N={len(X_train_current)})')
plt.plot(x_plot, y_predict_final, 'r-', linewidth=2, label='Kriging-Vorhersage')
plt.title('Kriging-Modell mit sequenzieller Optimierung der Hyperparameter')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()
print(f"\nFinal optimiertes Theta: {np.round(M_1.opt_theta_.item(), 4)}")
print(f"Final geschätzter globaler Mittelwert: {np.round(M_1.mu_hat_, 4)}")
# Der letzte optimierte Punkt auf dem Surrogat (x_new_infill) ist eine gute Schätzung des Optimums der Funktion.
print(f"Bester gefundener x-Wert (aus Surrogat-Optimierung): {np.round(surrogate_opt_result.x.item(), 3)}")
print(f"Zugehöriger y-Wert der Black-Box an diesem x: {np.round(f_black_box(surrogate_opt_result.x).item(), 3)}")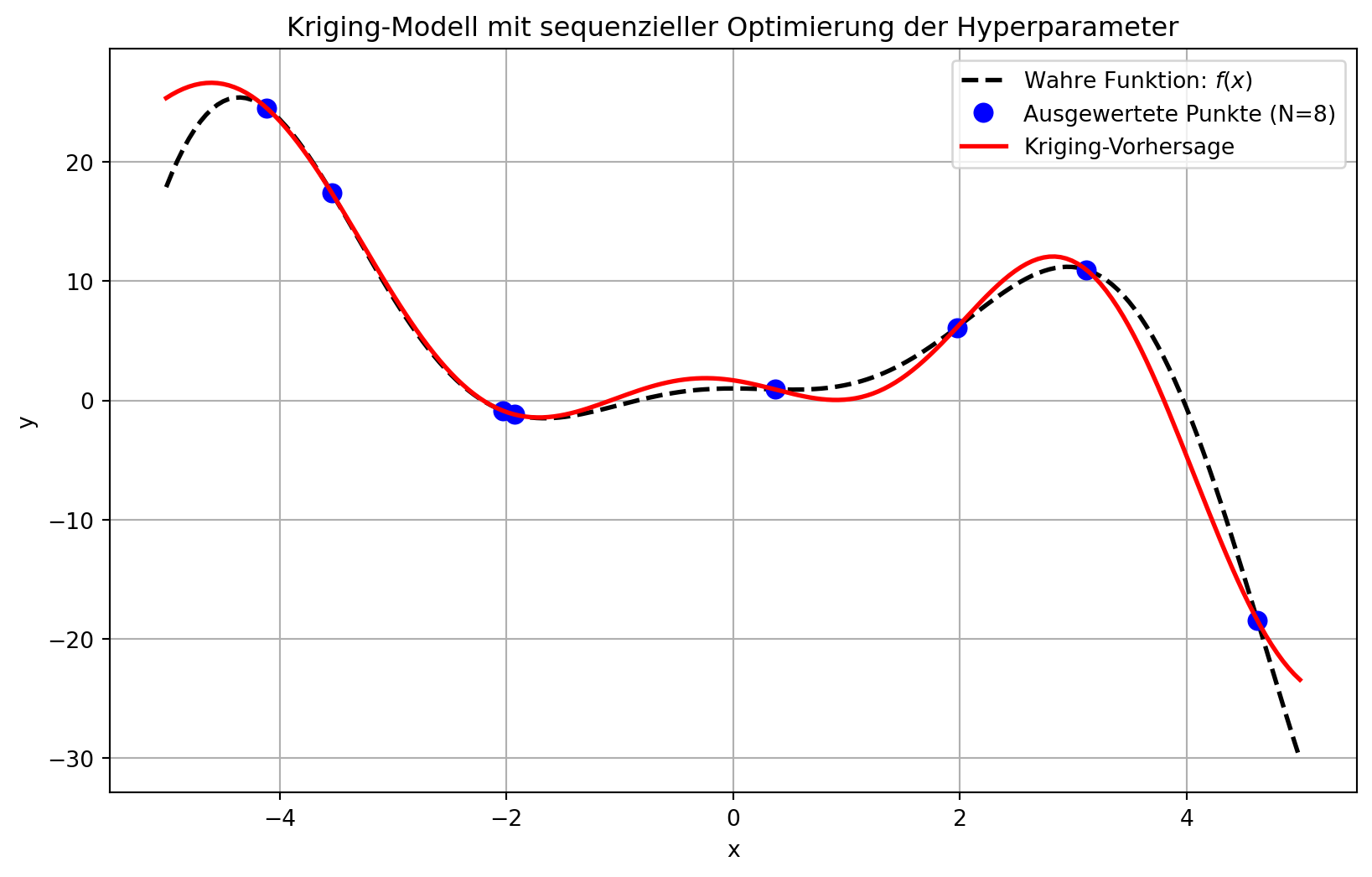
Final optimiertes Theta: -0.577
Final geschätzter globaler Mittelwert: 2.8055
Bester gefundener x-Wert (aus Surrogat-Optimierung): -1.93
Zugehöriger y-Wert der Black-Box an diesem x: -1.178