16  Using sklearn Surrogates in spotpython

Besides the internal kriging surrogate, which is used as a default by spotpython, any surrogate model from scikit-learn can be used as a surrogate in spotpython. This chapter explains how to use scikit-learn surrogates in spotpython.

import numpy as np
from math import inf
from spotpython.fun.objectivefunctions import Analytical
from spotpython.spot import Spot

16.1 Example: Branin Function with spotpython’s Internal Kriging Surrogate

16.1.1 The Objective Function Branin

  • The spotpython package provides several classes of objective functions.

  • We will use an analytical objective function, i.e., a function that can be described by a (closed) formula.

  • Here we will use the Branin function:

      y = a * (x2 - b * x1**2 + c * x1 - r) ** 2 + s * (1 - t) * np.cos(x1) + s,
  where values of a, b, c, r, s and t are: a = 1, b = 5.1 / (4*pi**2),
  c = 5 / pi, r = 6, s = 10 and t = 1 / (8*pi).

  • It has three global minima:

      f(x) = 0.397887 at (-pi, 12.275), (pi, 2.275), and (9.42478, 2.475).
from spotpython.fun.objectivefunctions import Analytical
fun = Analytical().fun_branin
NoteTensorBoard

Similar to the one-dimensional case, which was introduced in Section Section 12.25, we can use TensorBoard to monitor the progress of the optimization. We will use the same code, only the prefix is different:

from spotpython.utils.init import fun_control_init, design_control_init
PREFIX = "04"
fun_control = fun_control_init(
    PREFIX=PREFIX,
    lower = np.array([-5,-0]),
    upper = np.array([10,15]),
    fun_evals=20,
    max_time=inf)

design_control = design_control_init(
    init_size=10)

16.1.2 Running the surrogate model based optimizer Spot:

spot_2 = Spot(fun=fun,
                   fun_control=fun_control,
                   design_control=design_control)
spot_2.run()
spotpython tuning: 3.8004525569254524 [######----] 55.00%. Success rate: 100.00% 
spotpython tuning: 3.8004525569254524 [######----] 60.00%. Success rate: 50.00% 
spotpython tuning: 3.1644860748767325 [######----] 65.00%. Success rate: 66.67% 
spotpython tuning: 3.1405013986990866 [#######---] 70.00%. Success rate: 75.00% 
spotpython tuning: 3.0703215884465367 [########--] 75.00%. Success rate: 80.00% 
spotpython tuning: 2.934924209020851 [########--] 80.00%. Success rate: 83.33% 
spotpython tuning: 0.4523710119285411 [########--] 85.00%. Success rate: 85.71% 
spotpython tuning: 0.4335054313511062 [#########-] 90.00%. Success rate: 87.50% 
spotpython tuning: 0.39841709590731966 [##########] 95.00%. Success rate: 88.89% 
spotpython tuning: 0.39796888979727996 [##########] 100.00%. Success rate: 90.00% Done...

Experiment saved to 04_res.pkl
<spotpython.spot.spot.Spot at 0x1080e4050>

16.1.3 TensorBoard

Now we can start TensorBoard in the background with the following command:

tensorboard --logdir="./runs"

We can access the TensorBoard web server with the following URL:

http://localhost:6006/

The TensorBoard plot illustrates how spotpython can be used as a microscope for the internal mechanisms of the surrogate-based optimization process. Here, one important parameter, the learning rate \(\theta\) of the Kriging surrogate is plotted against the number of optimization steps.

TensorBoard visualization of the spotpython optimization process and the surrogate model.

16.1.5 Show the Progress and the Surrogate

spot_2.plot_progress(log_y=True)

spot_2.surrogate.plot()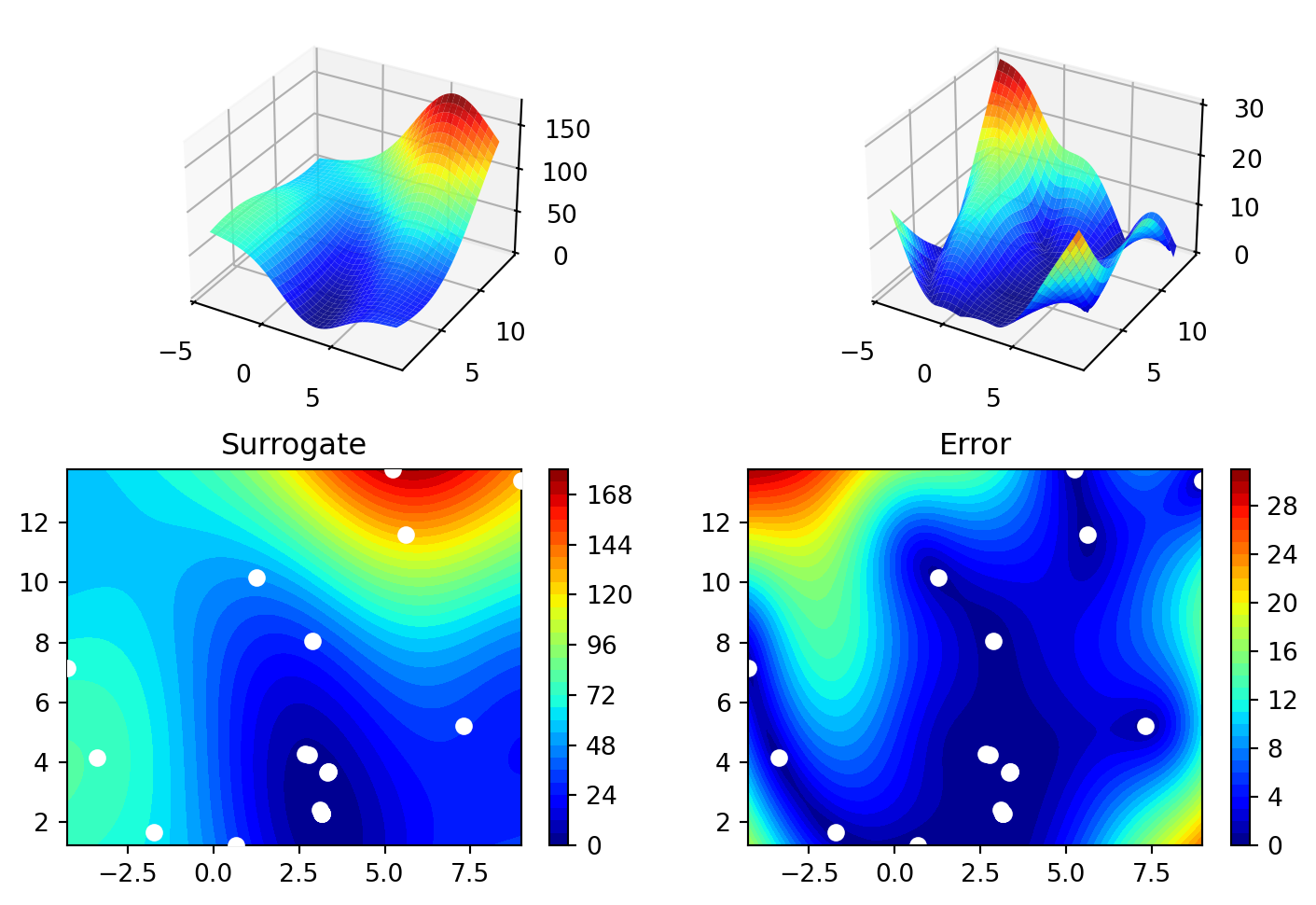

16.2 Example: Using Surrogates From scikit-learn

  • Default is the spotpython (i.e., the internal) kriging surrogate.
  • It can be called explicitely and passed to Spot.
from spotpython.surrogate.kriging import Kriging
S_0 = Kriging(name='kriging', seed=123)
  • Alternatively, models from scikit-learn can be selected, e.g., Gaussian Process, RBFs, Regression Trees, etc.
# Needed for the sklearn surrogates:
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import RBF
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn import linear_model
from sklearn import tree
import pandas as pd
  • Here are some additional models that might be useful later:
S_Tree = DecisionTreeRegressor(random_state=0)
S_LM = linear_model.LinearRegression()
S_Ridge = linear_model.Ridge()
S_RF = RandomForestRegressor(max_depth=2, random_state=0)

16.2.1 GaussianProcessRegressor as a Surrogate

  • To use a Gaussian Process model from sklearn, that is similar to spotpython’s Kriging, we can proceed as follows:
kernel = 1 * RBF(length_scale=1.0, length_scale_bounds=(1e-2, 1e2))
S_GP = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=9)

  • The scikit-learn GP model S_GP is selected for Spot as follows:

    surrogate = S_GP

  • We can check the kind of surogate model with the command isinstance:

isinstance(S_GP, GaussianProcessRegressor) 
True
isinstance(S_0, Kriging)
True
  • Similar to the Spot run with the internal Kriging model, we can call the run with the scikit-learn surrogate:
fun = Analytical(seed=123).fun_branin
spot_2_GP = Spot(fun=fun,
                     fun_control=fun_control,
                     design_control=design_control,
                     surrogate = S_GP)
spot_2_GP.run()
spotpython tuning: 18.865094417928255 [######----] 55.00%. Success rate: 100.00% 
spotpython tuning: 4.066951764659748 [######----] 60.00%. Success rate: 100.00% 
spotpython tuning: 3.4618268978622053 [######----] 65.00%. Success rate: 100.00% 
spotpython tuning: 3.4618268978622053 [#######---] 70.00%. Success rate: 75.00% 
spotpython tuning: 1.328427129373333 [########--] 75.00%. Success rate: 80.00% 
spotpython tuning: 0.9549984699881495 [########--] 80.00%. Success rate: 83.33% 
spotpython tuning: 0.9351546756190547 [########--] 85.00%. Success rate: 85.71% 
spotpython tuning: 0.3997498980904961 [#########-] 90.00%. Success rate: 87.50% 
spotpython tuning: 0.398303602593181 [##########] 95.00%. Success rate: 88.89% 
spotpython tuning: 0.3982354139382931 [##########] 100.00%. Success rate: 90.00% Done...

Experiment saved to 04_res.pkl
<spotpython.spot.spot.Spot at 0x16a99ad50>
spot_2_GP.plot_progress()

spot_2_GP.print_results()
min y: 0.3982354139382931
x0: 3.149733645254801
x1: 2.274124565582247
[['x0', np.float64(3.149733645254801)], ['x1', np.float64(2.274124565582247)]]

16.3 Example: One-dimensional Sphere Function With spotpython’s Kriging

  • In this example, we will use an one-dimensional function, which allows us to visualize the optimization process.
    • show_models= True is added to the argument list.
from spotpython.fun.objectivefunctions import Analytical
fun_control = fun_control_init(
    lower = np.array([-1]),
    upper = np.array([1]),
    fun_evals=10,
    max_time=inf,
    show_models= True,
    tolerance_x = np.sqrt(np.spacing(1)))
fun = Analytical(seed=123).fun_sphere
design_control = design_control_init(
    init_size=3)
spot_1 = Spot(fun=fun,
                    fun_control=fun_control,
                    design_control=design_control)
spot_1.run()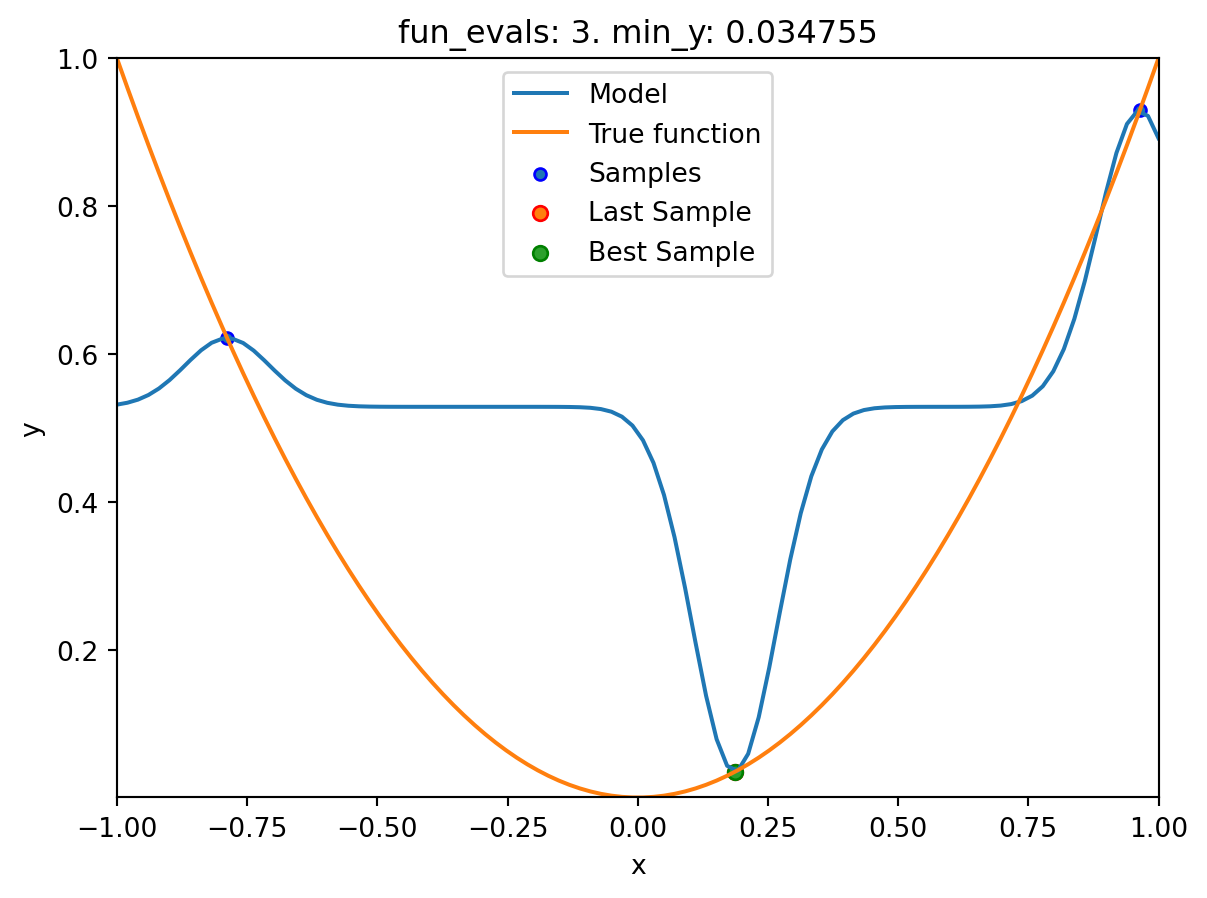

Using spacefilling design as fallback.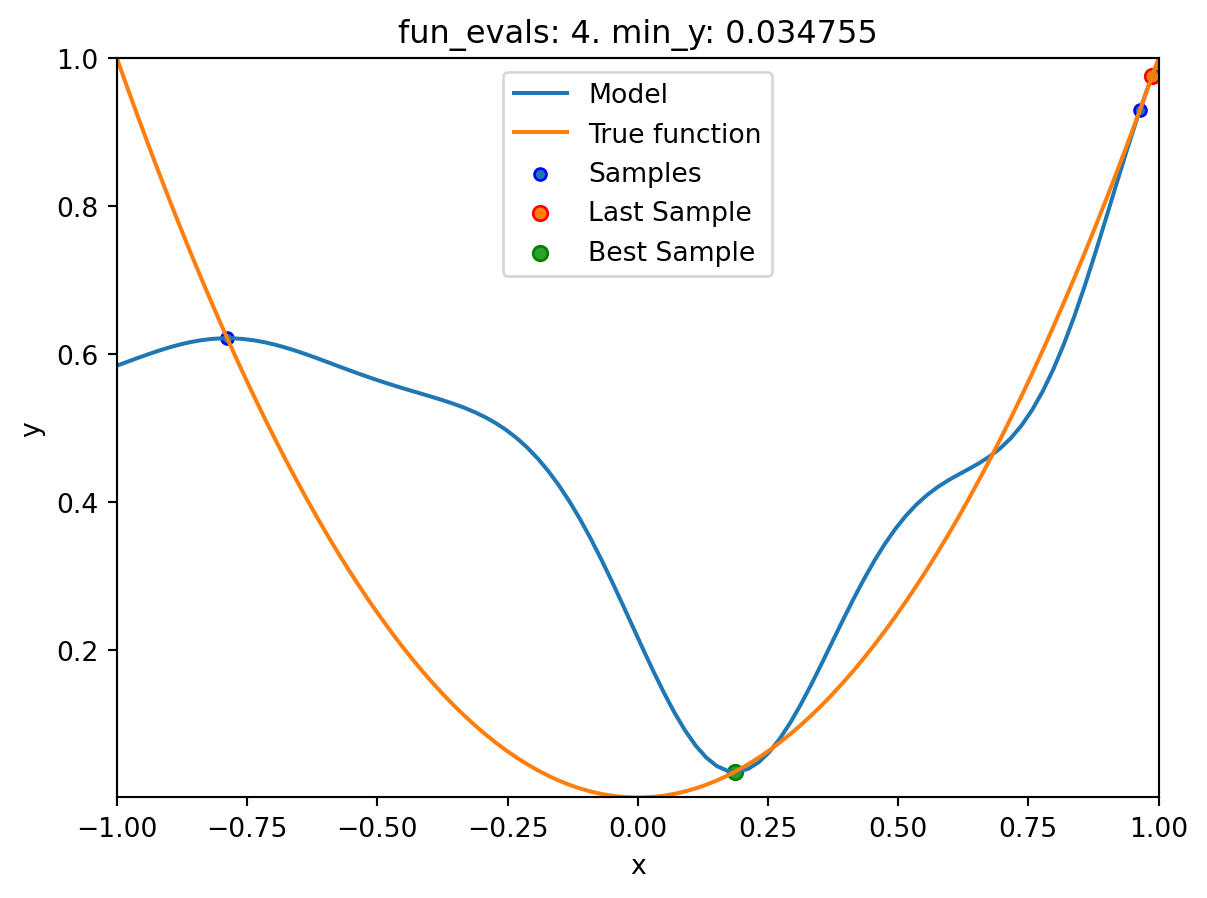

spotpython tuning: 0.03475493366922229 [####------] 40.00%. Success rate: 0.00% 

spotpython tuning: 0.03475493366922229 [#####-----] 50.00%. Success rate: 0.00%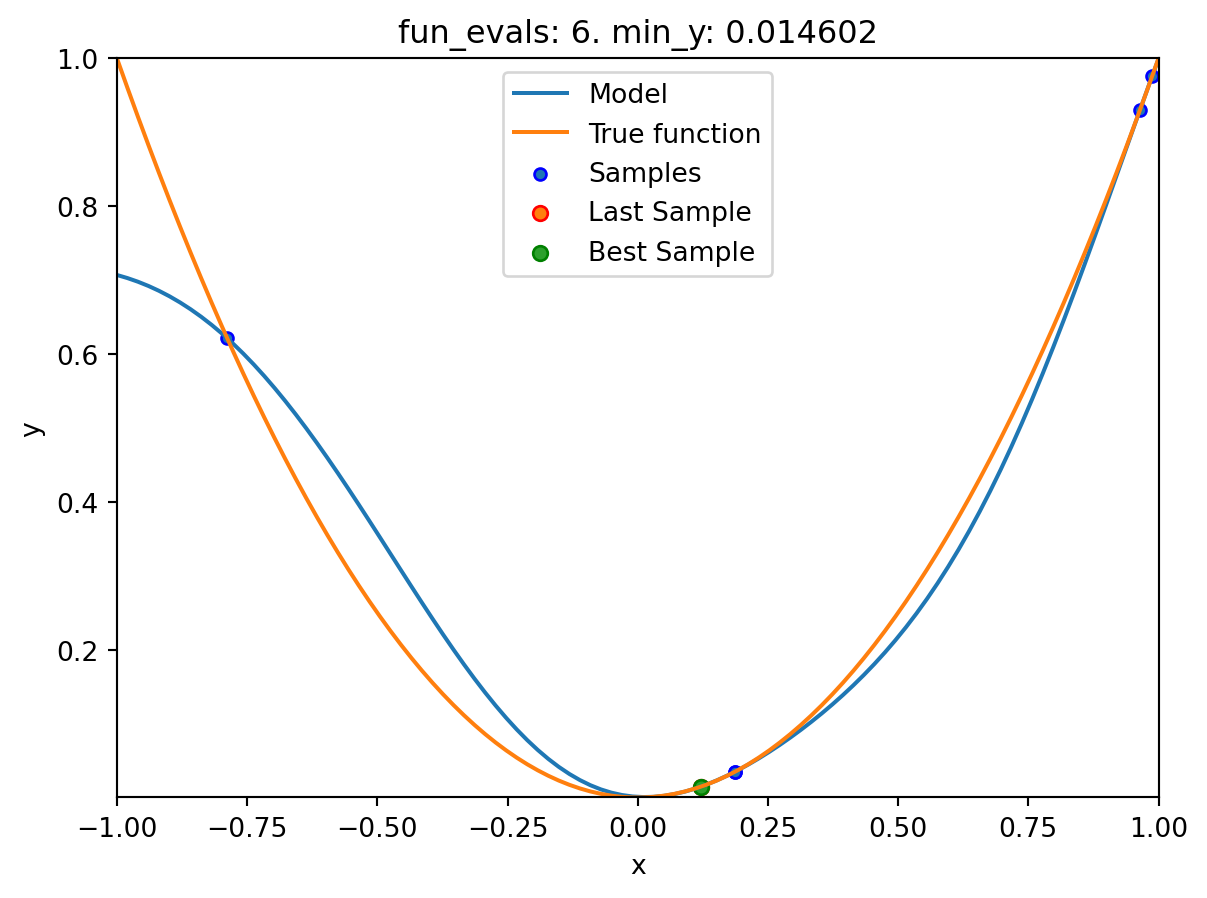 

spotpython tuning: 0.0002493578103496971 [######----] 60.00%. Success rate: 33.33%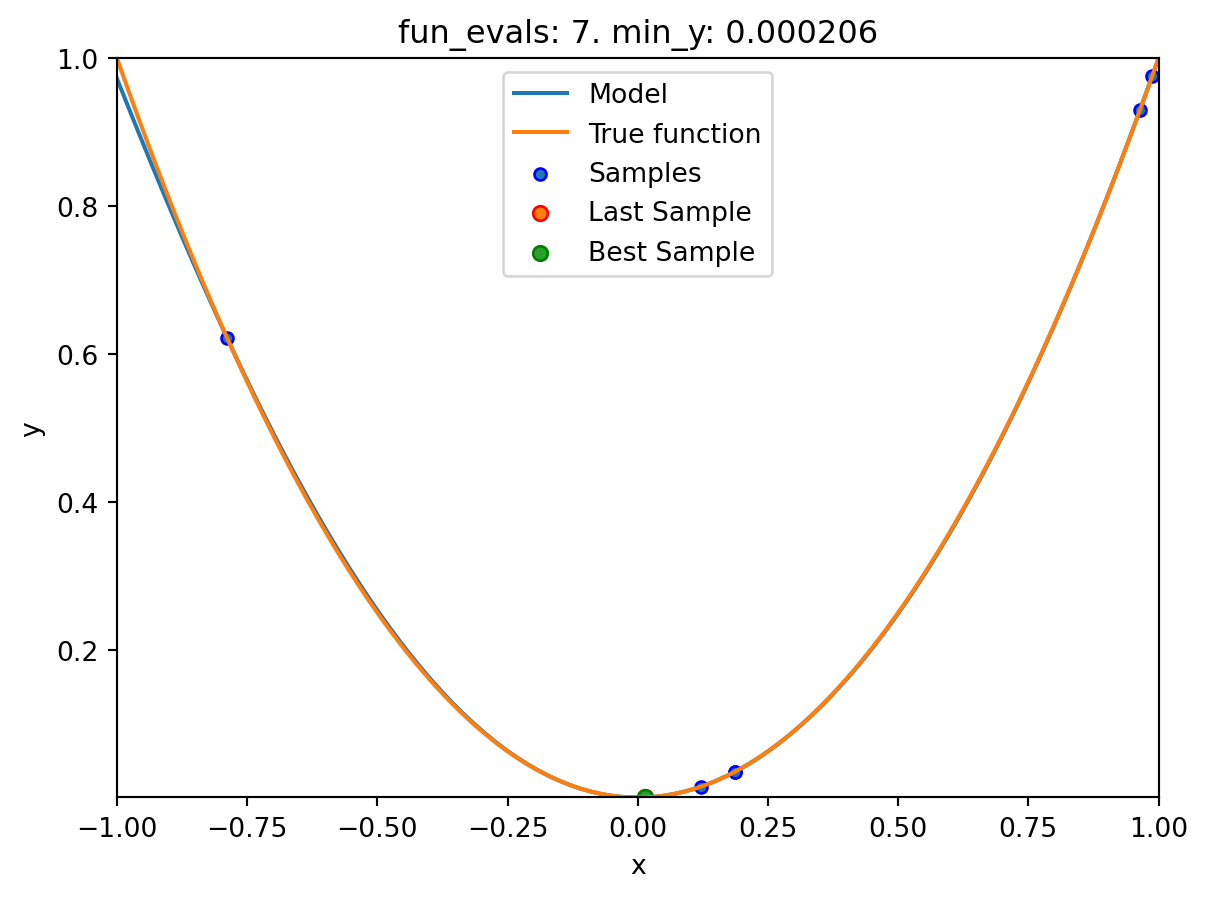 

spotpython tuning: 3.737005778245563e-07 [#######---] 70.00%. Success rate: 50.00%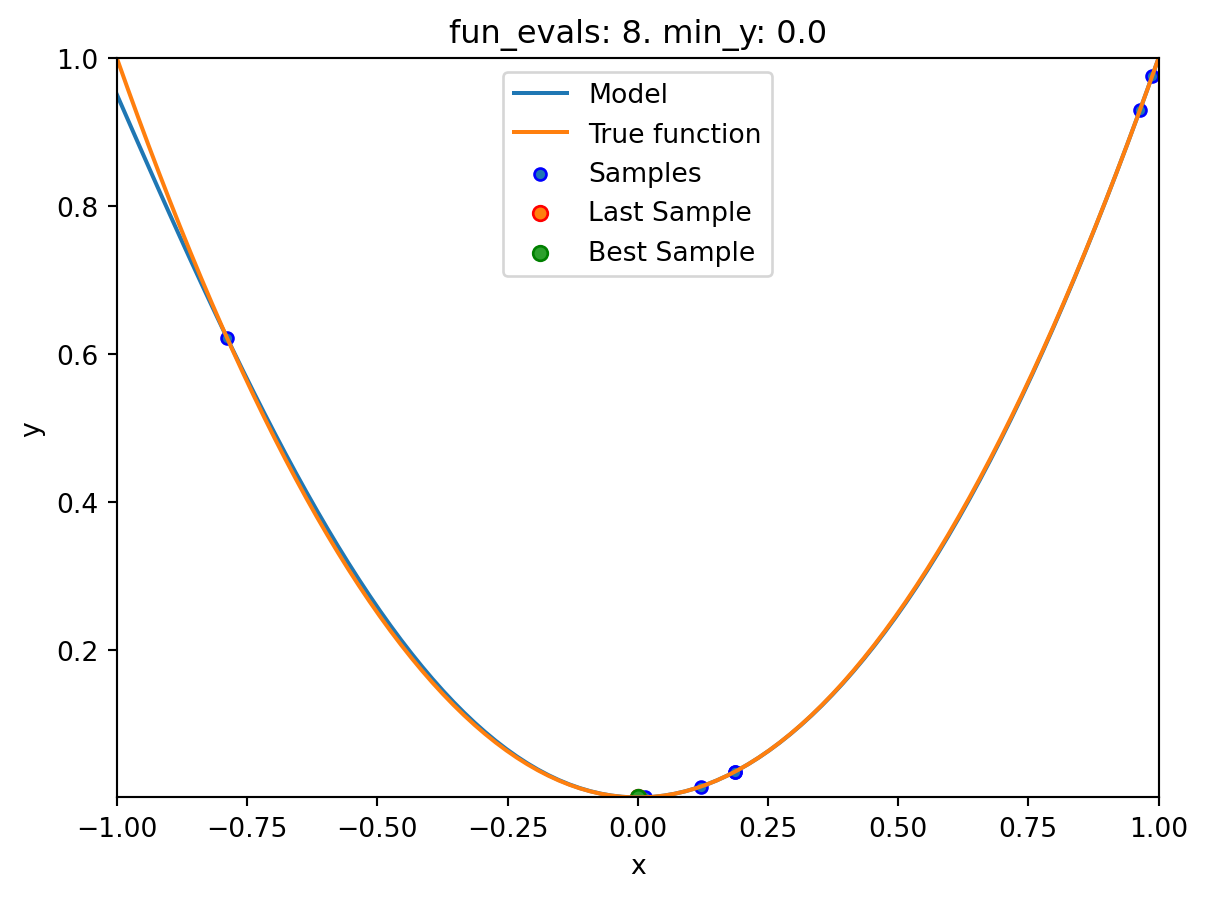 

spotpython tuning: 9.313071592223354e-08 [########--] 80.00%. Success rate: 60.00%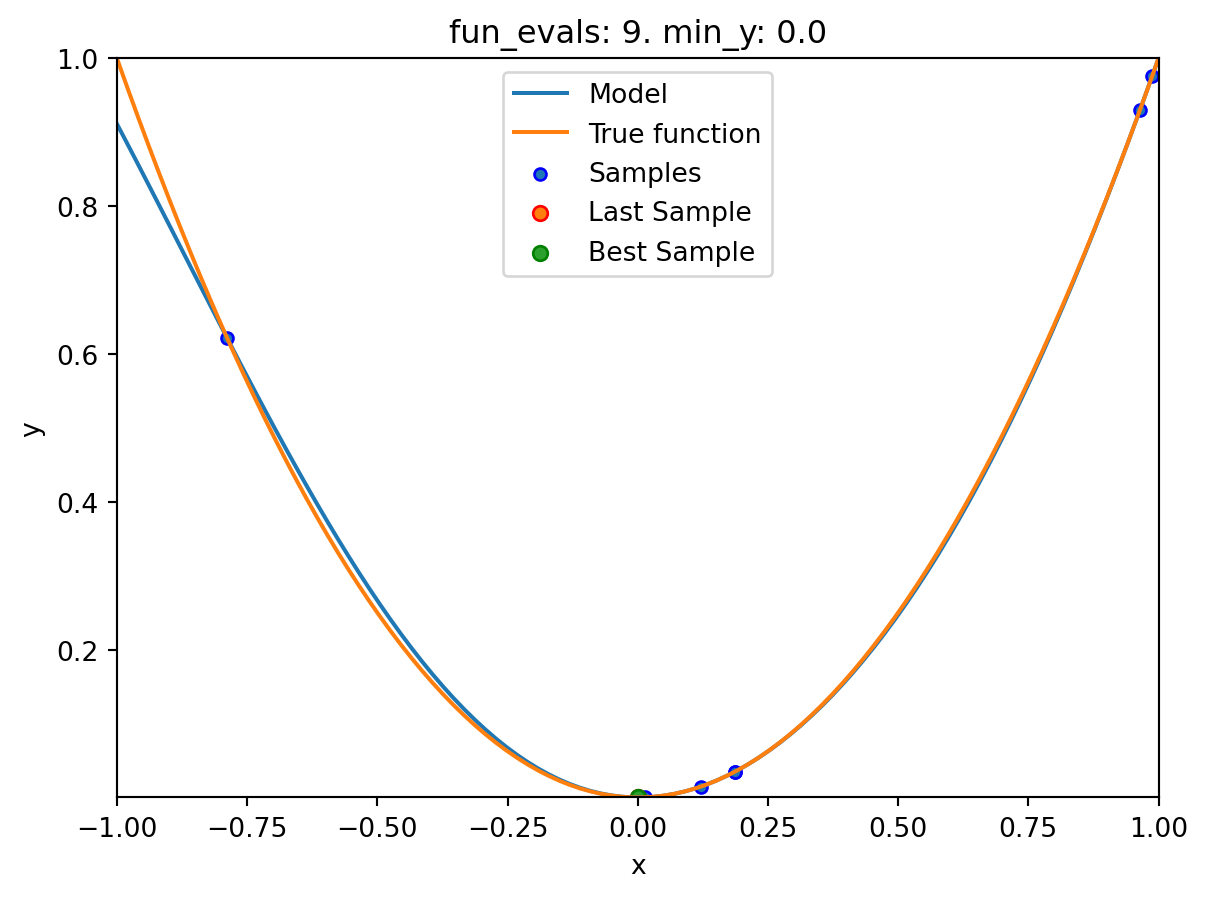 

spotpython tuning: 2.9997585469544003e-11 [#########-] 90.00%. Success rate: 66.67%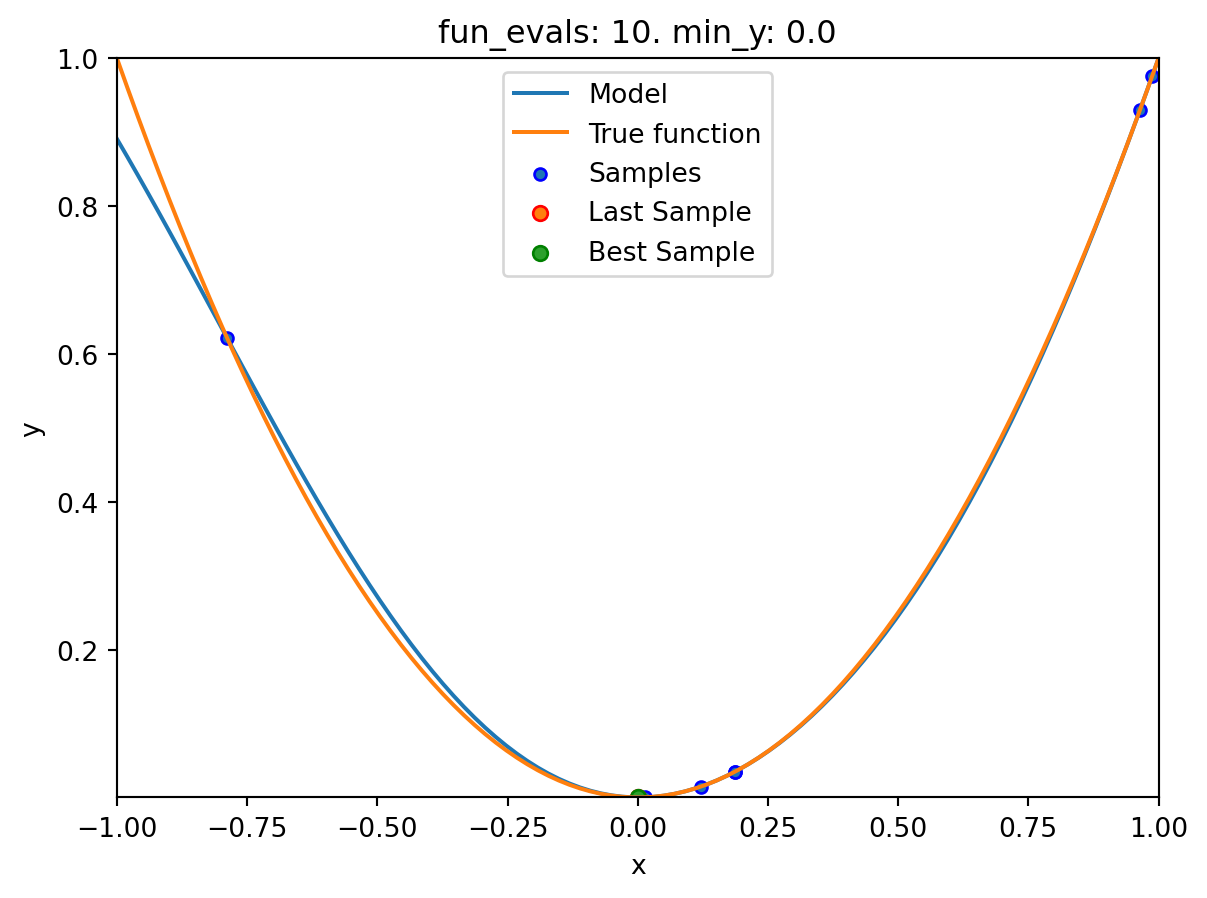 

spotpython tuning: 2.9997585469544003e-11 [##########] 100.00%. Success rate: 57.14% Done...

Experiment saved to 000_res.pkl

16.3.1 Results

spot_1.print_results()
min y: 2.9997585469544003e-11
x0: -5.477005155150395e-06
[['x0', np.float64(-5.477005155150395e-06)]]
spot_1.plot_progress(log_y=True)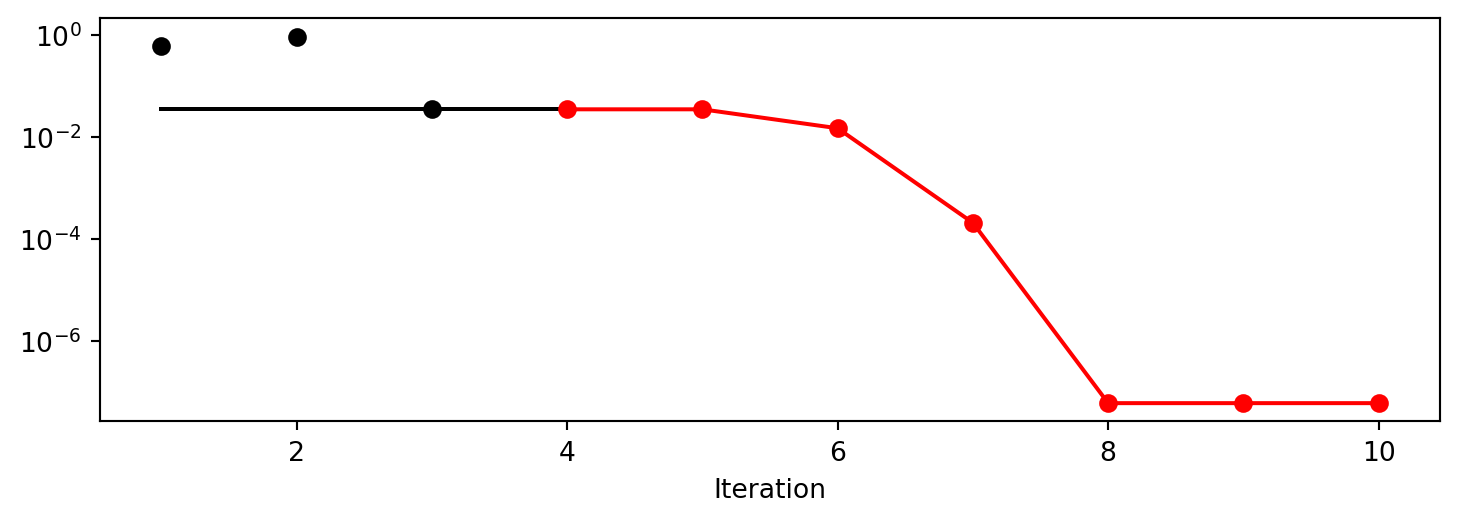

  • The method plot_model plots the final surrogate:
spot_1.plot_model()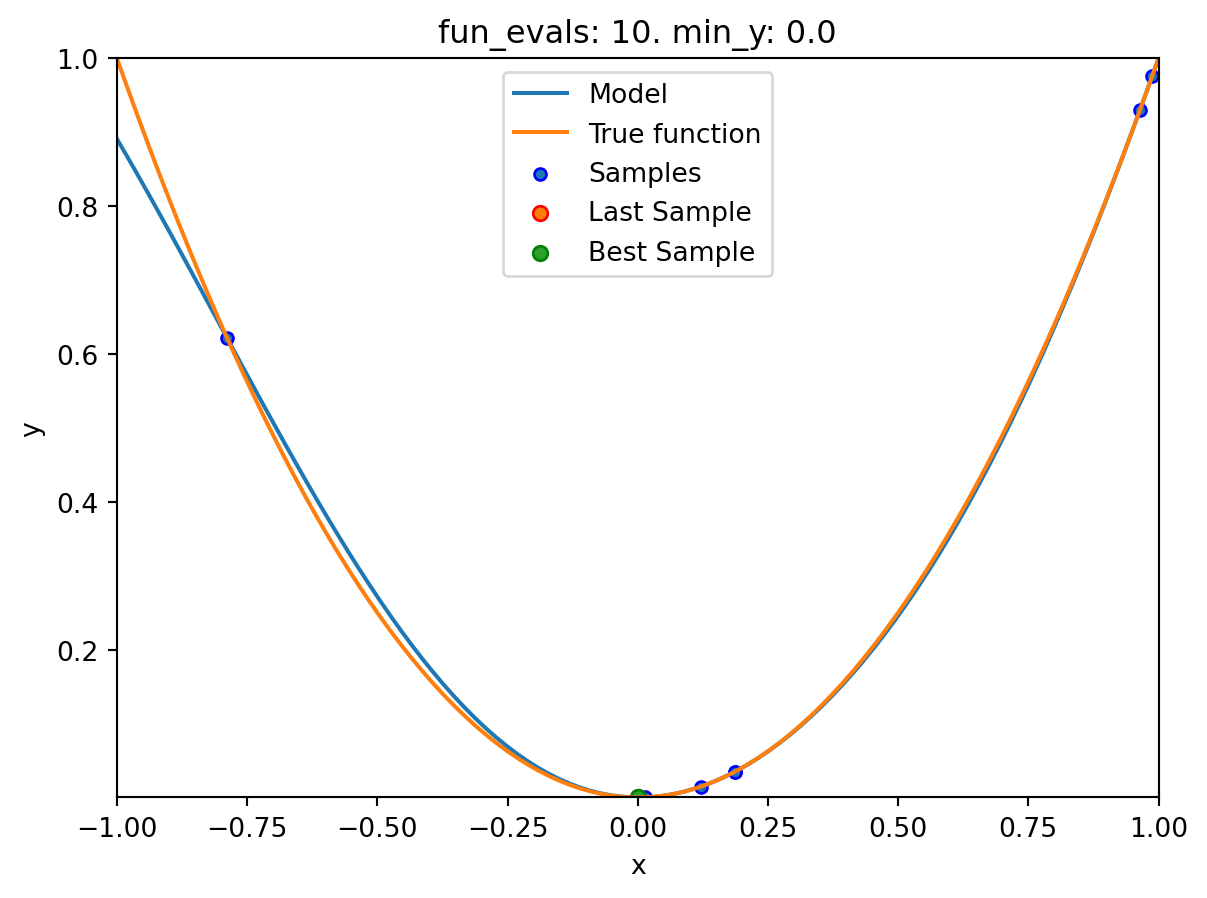

16.4 Example: Sklearn Model GaussianProcess

  • This example visualizes the search process on the GaussianProcessRegression surrogate from sklearn.
  • Therefore surrogate = S_GP is added to the argument list.
fun = Analytical(seed=123).fun_sphere
spot_1_GP = Spot(fun=fun,
                      fun_control=fun_control,
                      design_control=design_control,
                      surrogate = S_GP)
spot_1_GP.run()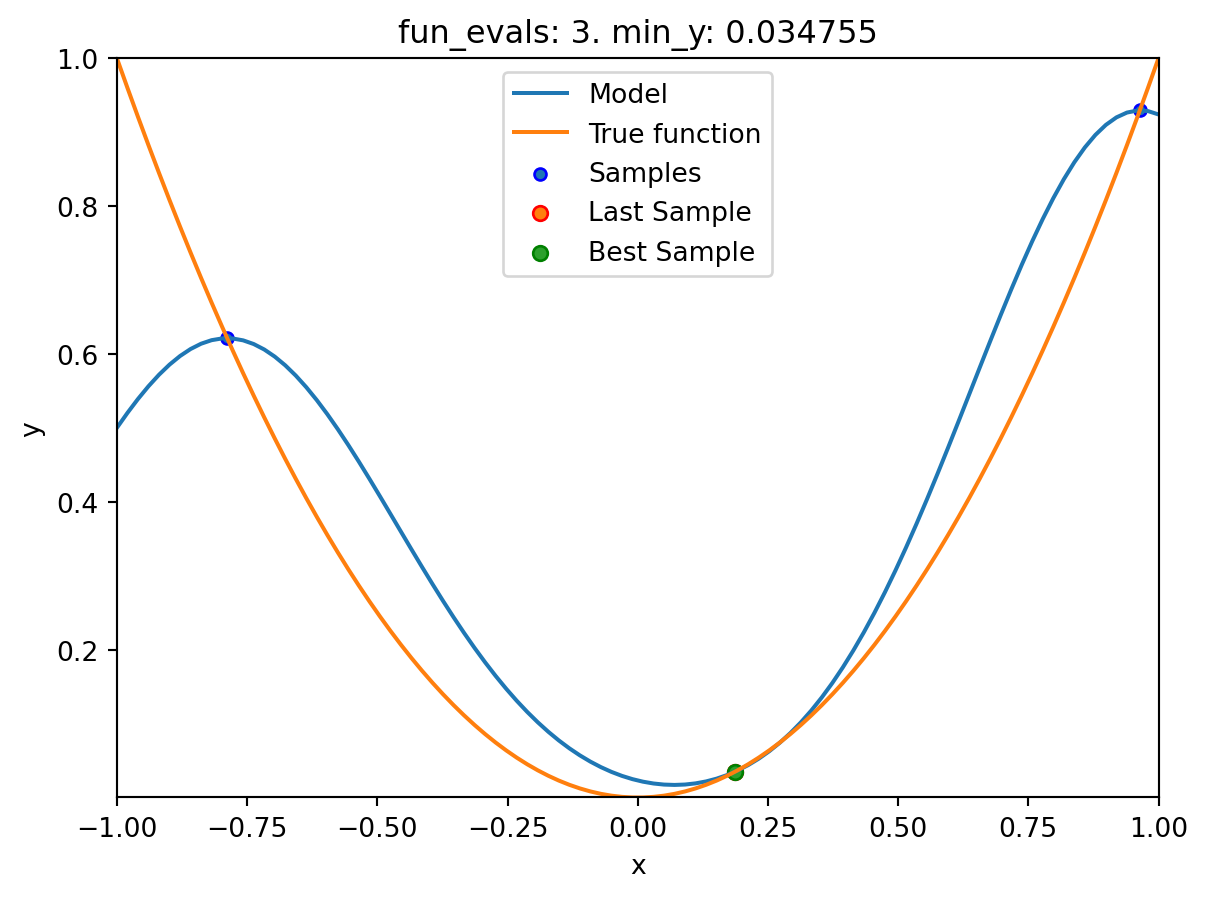

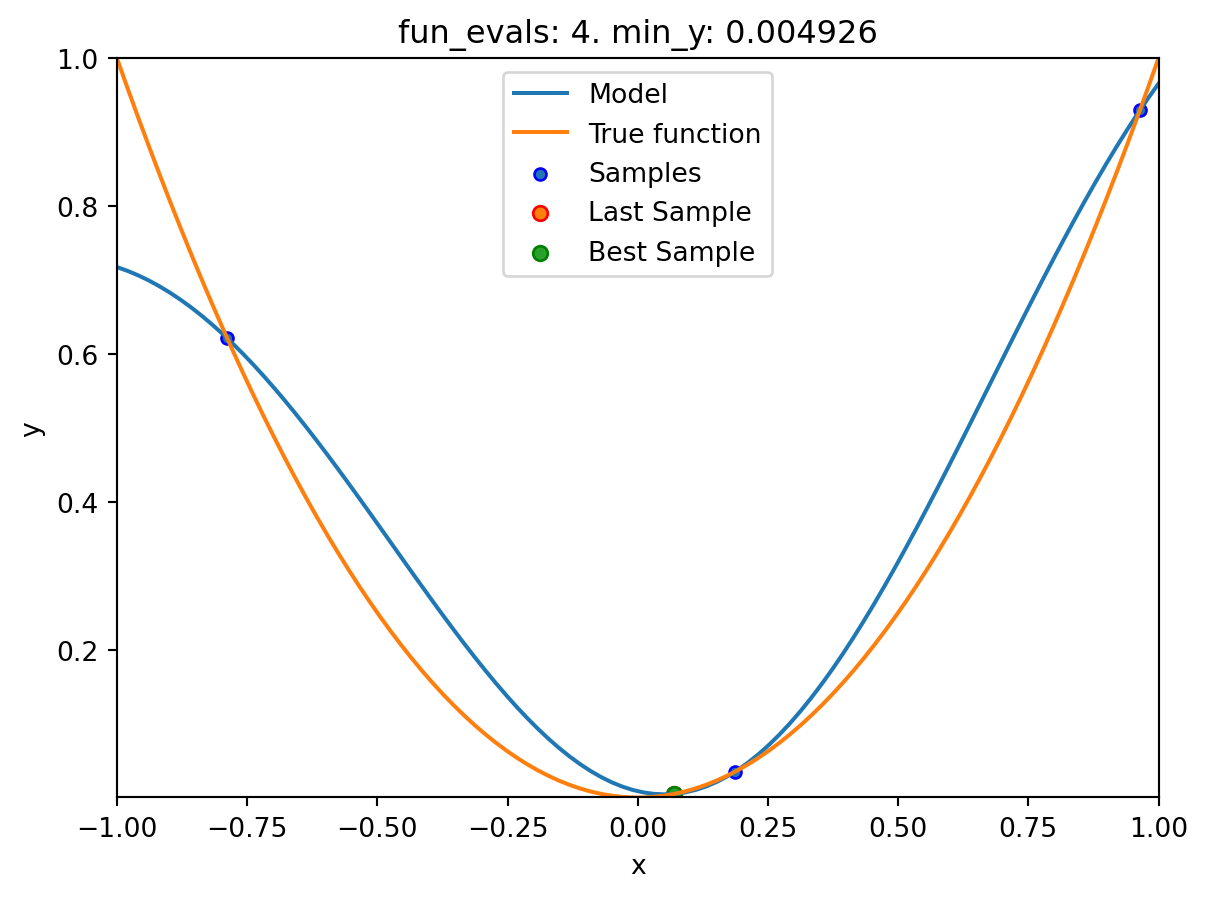
spotpython tuning: 0.004925671398319439 [####------] 40.00%. Success rate: 100.00%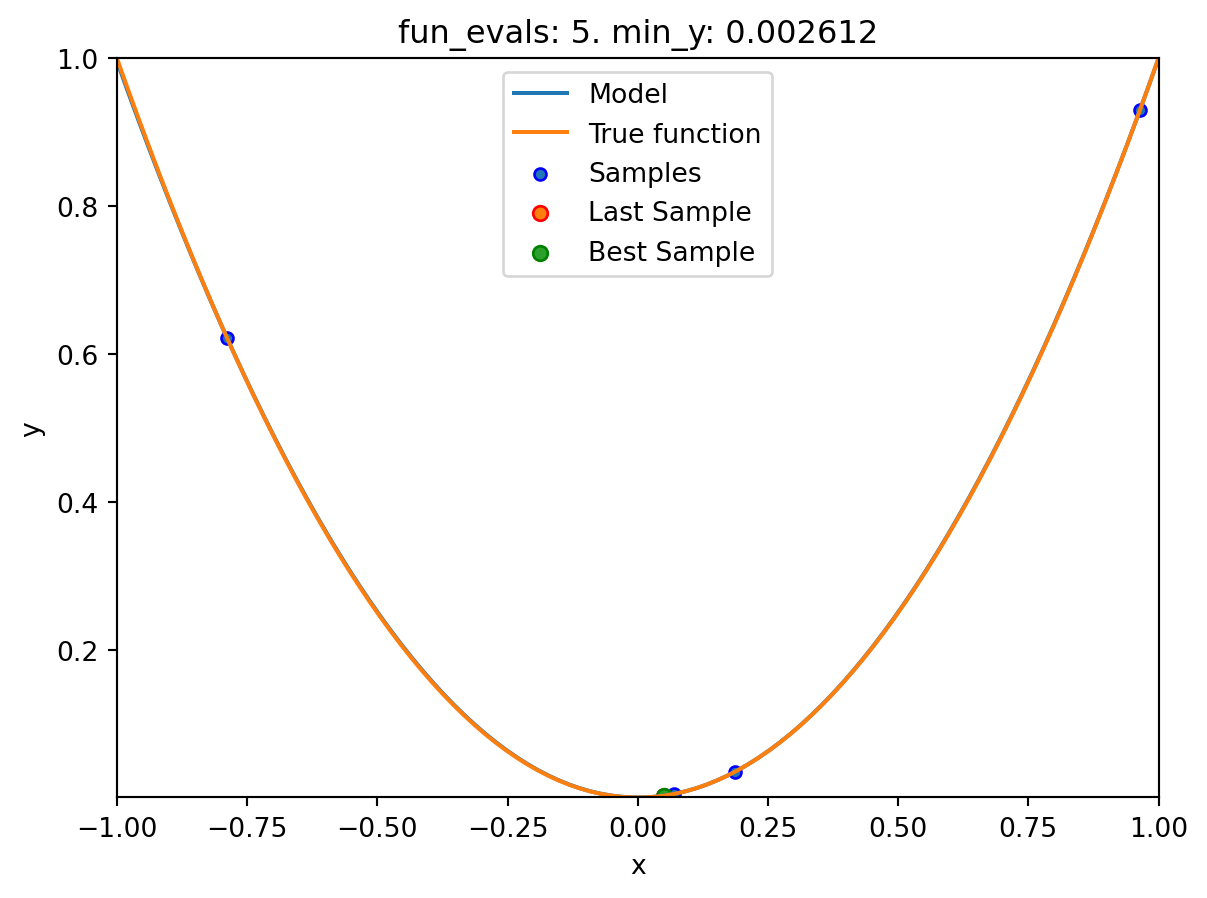 

spotpython tuning: 0.00261206235804241 [#####-----] 50.00%. Success rate: 100.00%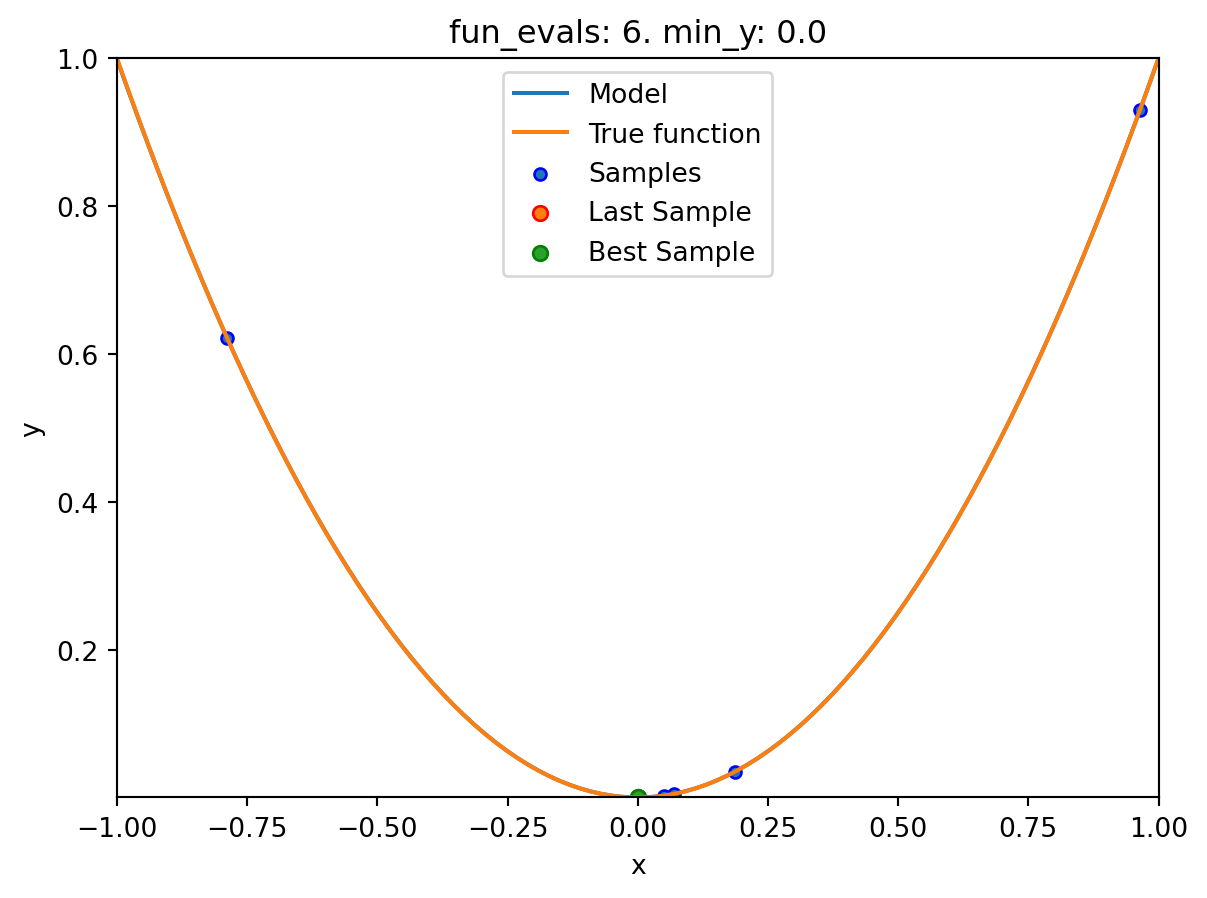 

spotpython tuning: 6.30724685184118e-07 [######----] 60.00%. Success rate: 100.00% 

spotpython tuning: 8.015822937486393e-08 [#######---] 70.00%. Success rate: 100.00%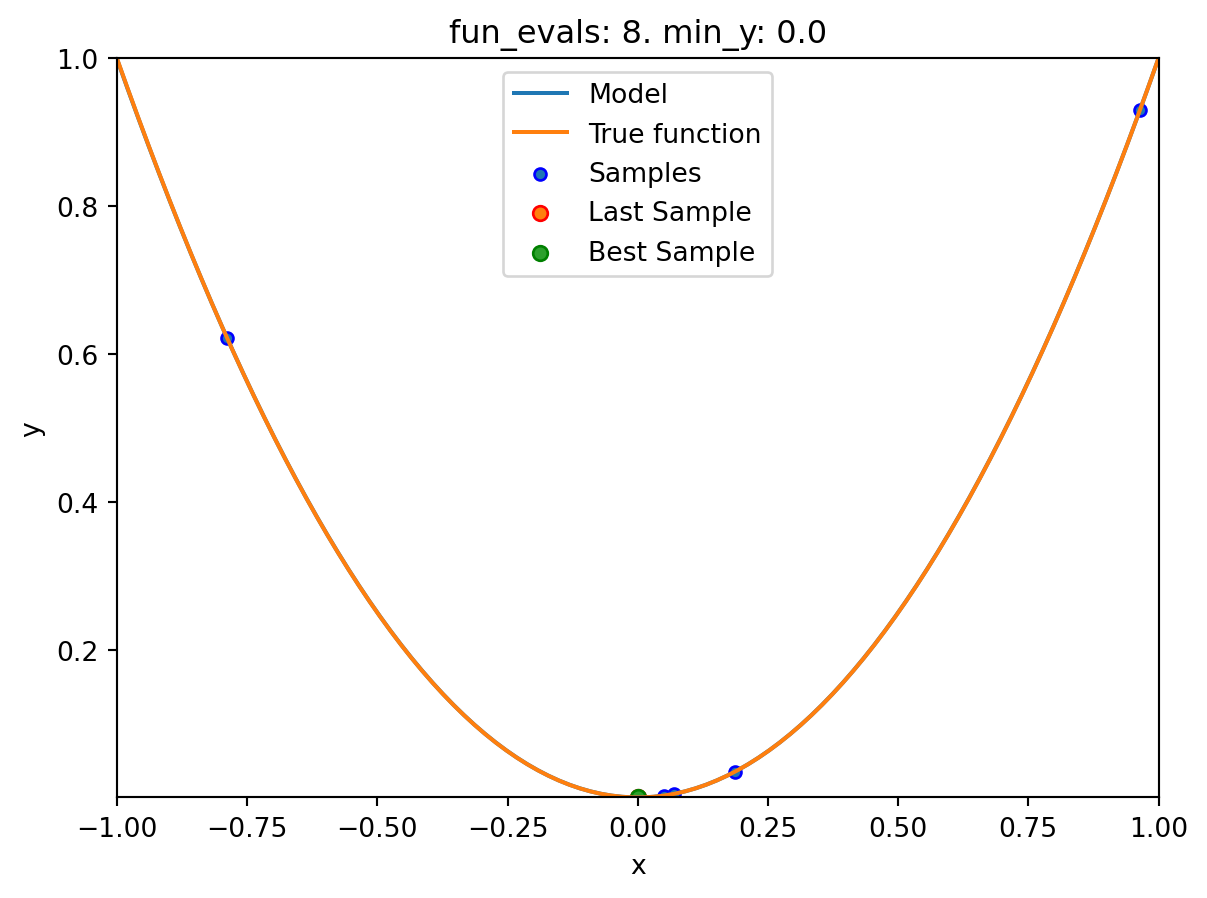 

spotpython tuning: 8.015822937486393e-08 [########--] 80.00%. Success rate: 80.00%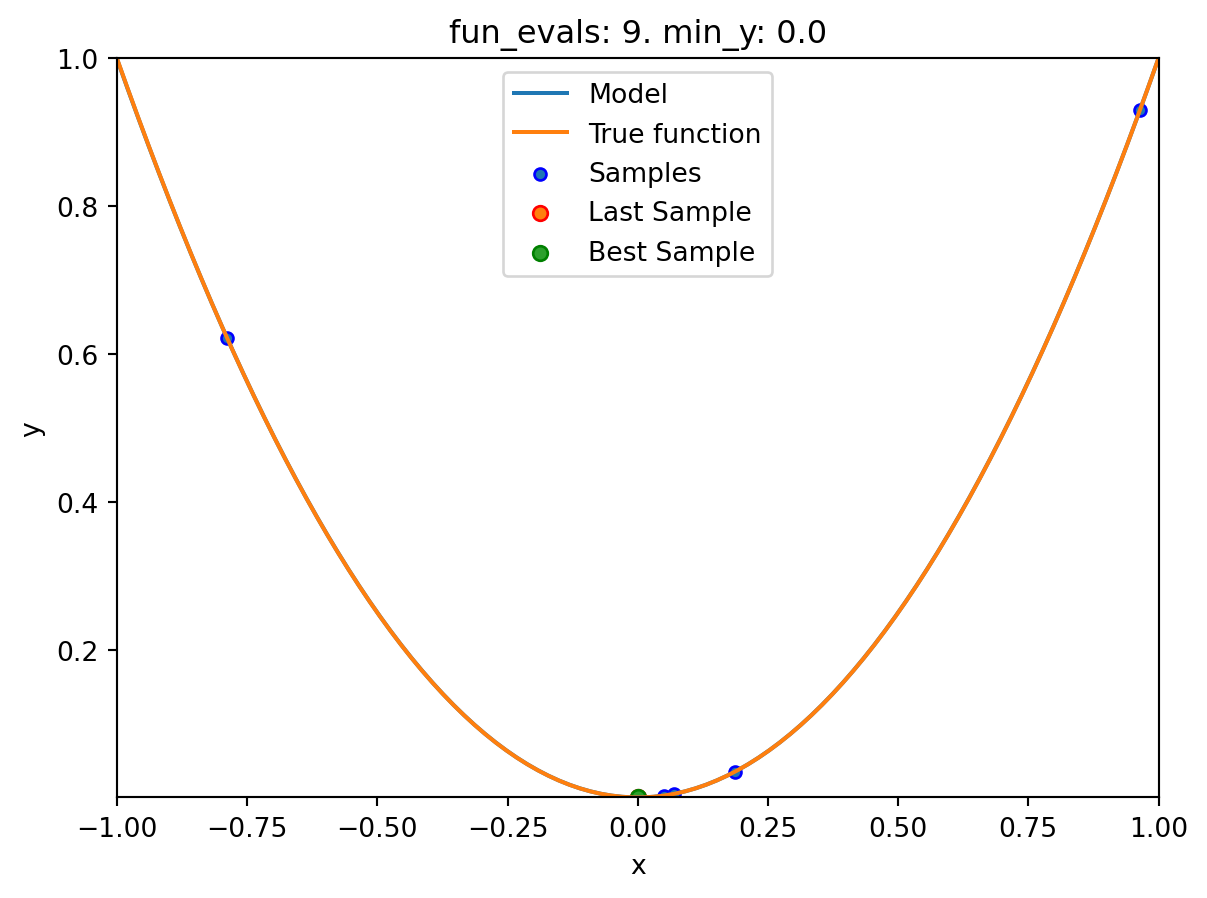 

spotpython tuning: 6.369177036405373e-09 [#########-] 90.00%. Success rate: 83.33%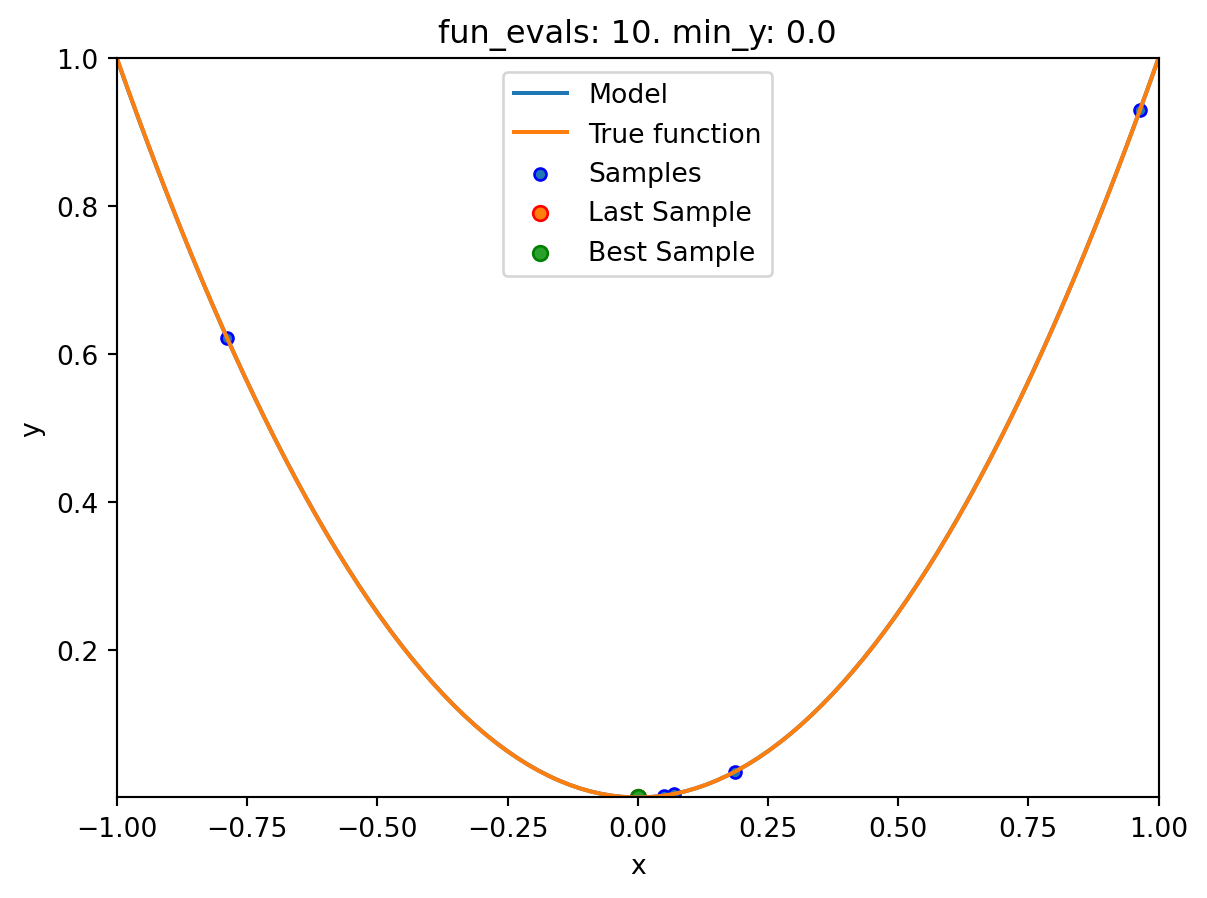 

spotpython tuning: 2.0638361689231364e-09 [##########] 100.00%. Success rate: 85.71% Done...

Experiment saved to 000_res.pkl
spot_1_GP.print_results()
min y: 2.0638361689231364e-09
x0: -4.5429463665369596e-05
[['x0', np.float64(-4.5429463665369596e-05)]]
spot_1_GP.plot_progress(log_y=True)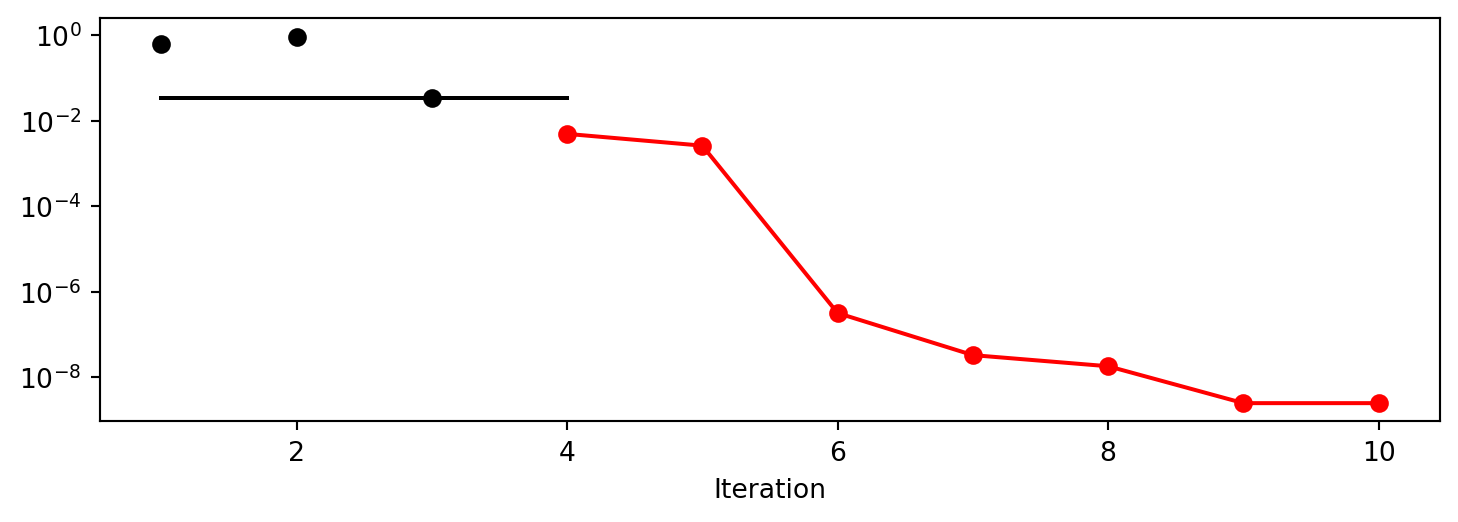

spot_1_GP.plot_model()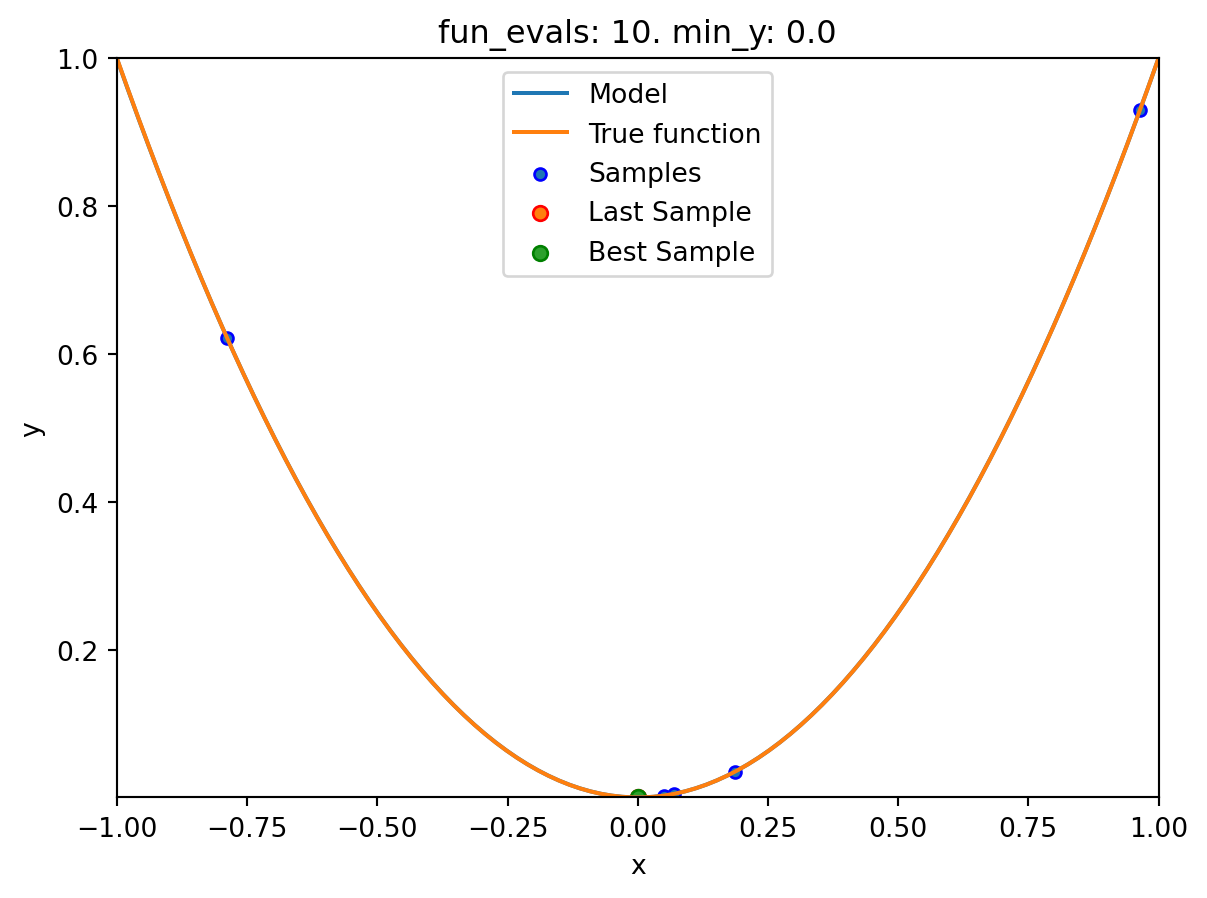

16.5 Exercises

16.5.1 1. A decision tree regressor: DecisionTreeRegressor

  • Describe the surrogate model. Use the information from the scikit-learn documentation.
  • Use the surrogate as the model for optimization.

16.5.2 2. A random forest regressor: RandomForestRegressor

  • Describe the surrogate model. Use the information from the scikit-learn documentation.
  • Use the surrogate as the model for optimization.

16.5.3 3. Ordinary least squares Linear Regression: LinearRegression

  • Describe the surrogate model. Use the information from the scikit-learn documentation.
  • Use the surrogate as the model for optimization.

16.5.4 4. Linear least squares with l2 regularization: Ridge

  • Describe the surrogate model. Use the information from the scikit-learn documentation.
  • Use the surrogate as the model for optimization.

16.5.5 5. Gradient Boosting: HistGradientBoostingRegressor

  • Describe the surrogate model. Use the information from the scikit-learn documentation.
  • Use the surrogate as the model for optimization.

16.5.6 6. Comparison of Surrogates

  • Use the following two objective functions

    1. the 1-dim sphere function fun_sphere and
    2. the two-dim Branin function fun_branin:

    for a comparison of the performance of the five different surrogates:

    • spotpython’s internal Kriging
    • DecisionTreeRegressor
    • RandomForestRegressor
    • linear_model.LinearRegression
    • linear_model.Ridge.

  • Generate a table with the results (number of function evaluations, best function value, and best parameter vector) for each surrogate and each function as shown in Table 16.1.

Table 16.1: Result table
surrogate fun fun_evals max_time x_0 min_y Comments
Kriging fun_sphere 10 inf
Kriging fun_branin 10 inf
DecisionTreeRegressor fun_sphere 10 inf
… … … …
Ridge fun_branin 10 inf
  • Discuss the results. Which surrogate is the best for which function? Why?

16.6 Selected Solutions

16.6.1 Solution to Exercise Section 16.5.5: Gradient Boosting

16.6.1.1 Branin: Using SPOT

import numpy as np
from math import inf
from spotpython.fun.objectivefunctions import Analytical
from spotpython.utils.init import fun_control_init, design_control_init
from spotpython.spot import Spot
  • The Objective Function Branin
fun = Analytical().fun_branin
PREFIX = "BRANIN"
fun_control = fun_control_init(
    PREFIX=PREFIX,
    lower = np.array([-5,-0]),
    upper = np.array([10,15]),
    fun_evals=20,
    max_time=inf)

design_control = design_control_init(
    init_size=10)
  • Running the surrogate model based optimizer Spot:
spot_2 = Spot(fun=fun,
                   fun_control=fun_control,
                   design_control=design_control)
spot_2.run()
spotpython tuning: 3.8004525569254524 [######----] 55.00%. Success rate: 100.00% 
spotpython tuning: 3.8004525569254524 [######----] 60.00%. Success rate: 50.00% 
spotpython tuning: 3.1644860748767325 [######----] 65.00%. Success rate: 66.67% 
spotpython tuning: 3.1405013986990866 [#######---] 70.00%. Success rate: 75.00% 
spotpython tuning: 3.0703215884465367 [########--] 75.00%. Success rate: 80.00% 
spotpython tuning: 2.934924209020851 [########--] 80.00%. Success rate: 83.33% 
spotpython tuning: 0.4523710119285411 [########--] 85.00%. Success rate: 85.71% 
spotpython tuning: 0.4335054313511062 [#########-] 90.00%. Success rate: 87.50% 
spotpython tuning: 0.39841709590731966 [##########] 95.00%. Success rate: 88.89% 
spotpython tuning: 0.39796888979727996 [##########] 100.00%. Success rate: 90.00% Done...

Experiment saved to BRANIN_res.pkl
<spotpython.spot.spot.Spot at 0x1740e6c10>
  • Print the results
spot_2.print_results()
min y: 0.39796888979727996
x0: 3.140132672900477
x1: 2.26769501627711
[['x0', np.float64(3.140132672900477)], ['x1', np.float64(2.26769501627711)]]
  • Show the optimization progress:
spot_2.plot_progress(log_y=True)

  • Generate a surrogate model plot:
spot_2.surrogate.plot()

16.6.1.2 Branin: Using Surrogates From scikit-learn

  • The HistGradientBoostingRegressor model from scikit-learn is selected:
# Needed for the sklearn surrogates:
from sklearn.ensemble import HistGradientBoostingRegressor
import pandas as pd
S_XGB = HistGradientBoostingRegressor()
  • The scikit-learn XGB model S_XGB is selected for Spot as follows: surrogate = S_XGB.
  • Similar to the Spot run with the internal Kriging model, we can call the run with the scikit-learn surrogate:
fun = Analytical(seed=123).fun_branin
spot_2_XGB = Spot(fun=fun,
                     fun_control=fun_control,
                     design_control=design_control,
                     surrogate = S_XGB)
spot_2_XGB.run()
spotpython tuning: 30.69410528614059 [######----] 55.00%. Success rate: 0.00% 
Using spacefilling design as fallback.
spotpython tuning: 30.69410528614059 [######----] 60.00%. Success rate: 0.00% 
Using spacefilling design as fallback.
spotpython tuning: 30.69410528614059 [######----] 65.00%. Success rate: 0.00% 
Using spacefilling design as fallback.
spotpython tuning: 30.69410528614059 [#######---] 70.00%. Success rate: 0.00% 
Using spacefilling design as fallback.
spotpython tuning: 1.3263745845108854 [########--] 75.00%. Success rate: 20.00% 
Using spacefilling design as fallback.
spotpython tuning: 1.3263745845108854 [########--] 80.00%. Success rate: 16.67% 
Using spacefilling design as fallback.
spotpython tuning: 1.3263745845108854 [########--] 85.00%. Success rate: 14.29% 
Using spacefilling design as fallback.
spotpython tuning: 1.3263745845108854 [#########-] 90.00%. Success rate: 12.50% 
Using spacefilling design as fallback.
spotpython tuning: 1.3263745845108854 [##########] 95.00%. Success rate: 11.11% 
Using spacefilling design as fallback.
spotpython tuning: 1.3263745845108854 [##########] 100.00%. Success rate: 10.00% Done...

Experiment saved to BRANIN_res.pkl
<spotpython.spot.spot.Spot at 0x166d2ccd0>
  • Print the Results
spot_2_XGB.print_results()
min y: 1.3263745845108854
x0: -2.872730773493426
x1: 10.874313833535739
[['x0', np.float64(-2.872730773493426)],
 ['x1', np.float64(10.874313833535739)]]
  • Show the Progress
spot_2_XGB.plot_progress(log_y=True)

  • Since the sklearn model does not provide a plot method, we cannot generate a surrogate model plot.

16.6.1.3 One-dimensional Sphere Function With spotpython’s Kriging

  • In this example, we will use an one-dimensional function, which allows us to visualize the optimization process.
    • show_models= True is added to the argument list.
from spotpython.fun.objectivefunctions import Analytical
fun_control = fun_control_init(
    lower = np.array([-1]),
    upper = np.array([1]),
    fun_evals=10,
    max_time=inf,
    show_models= True,
    tolerance_x = np.sqrt(np.spacing(1)))
fun = Analytical(seed=123).fun_sphere
design_control = design_control_init(
    init_size=3)
spot_1 = Spot(fun=fun,
                    fun_control=fun_control,
                    design_control=design_control)
spot_1.run()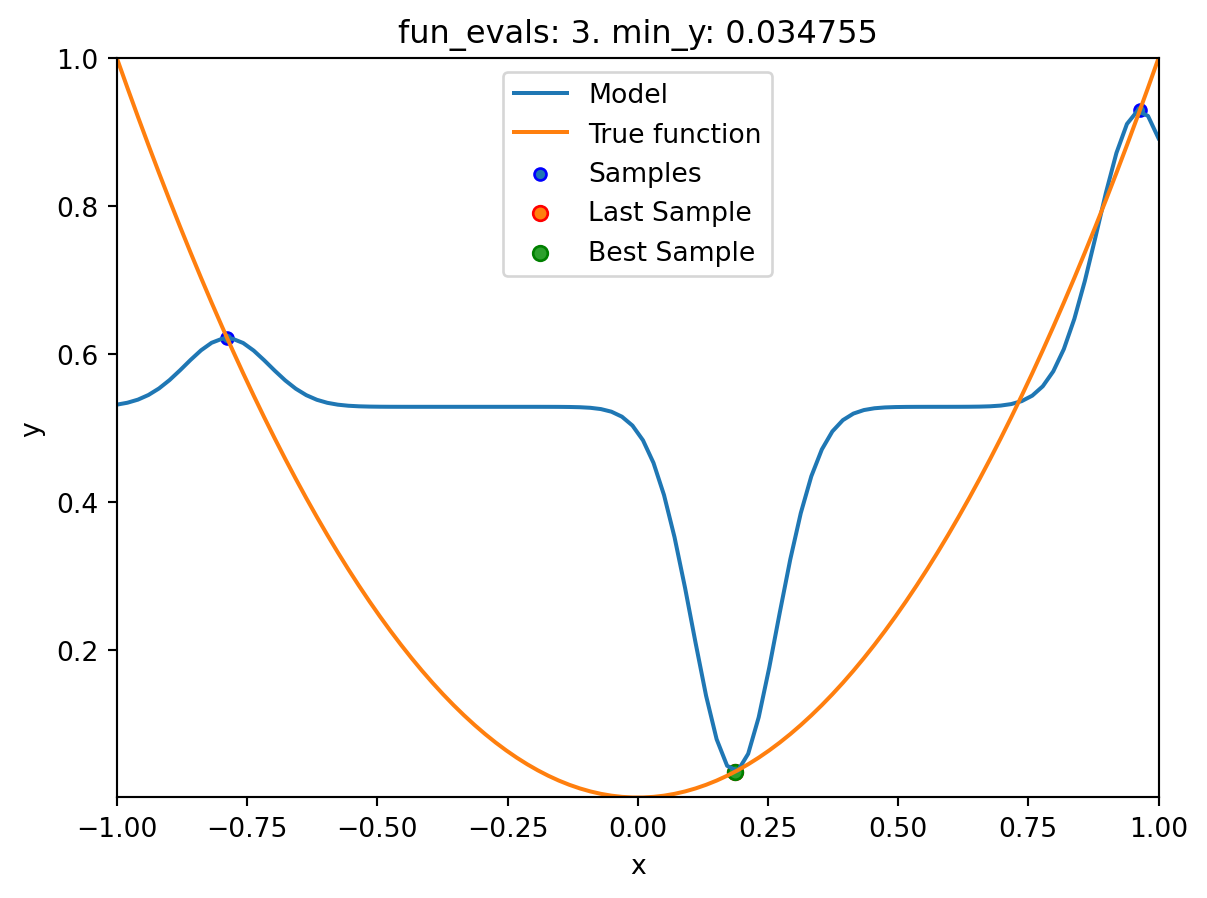

Using spacefilling design as fallback.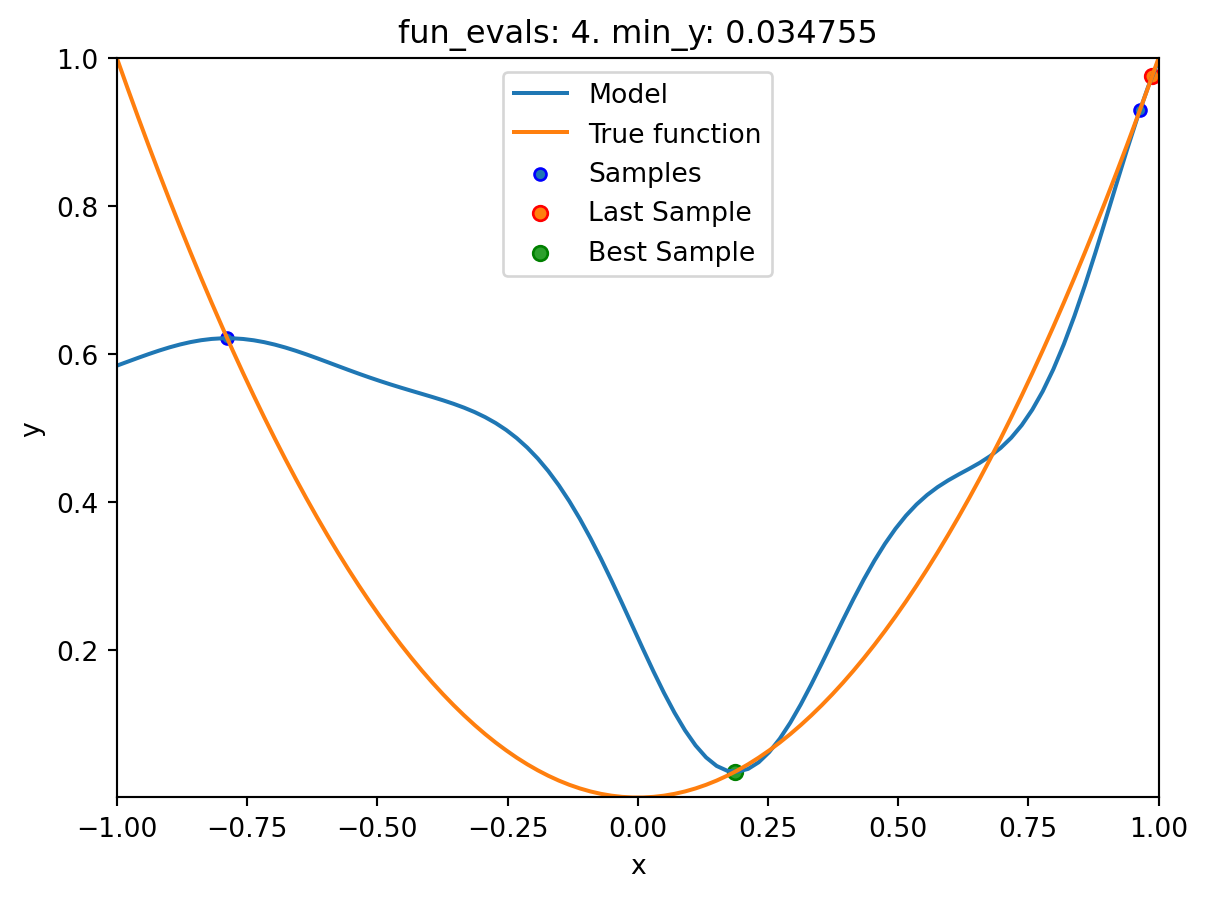

spotpython tuning: 0.03475493366922229 [####------] 40.00%. Success rate: 0.00%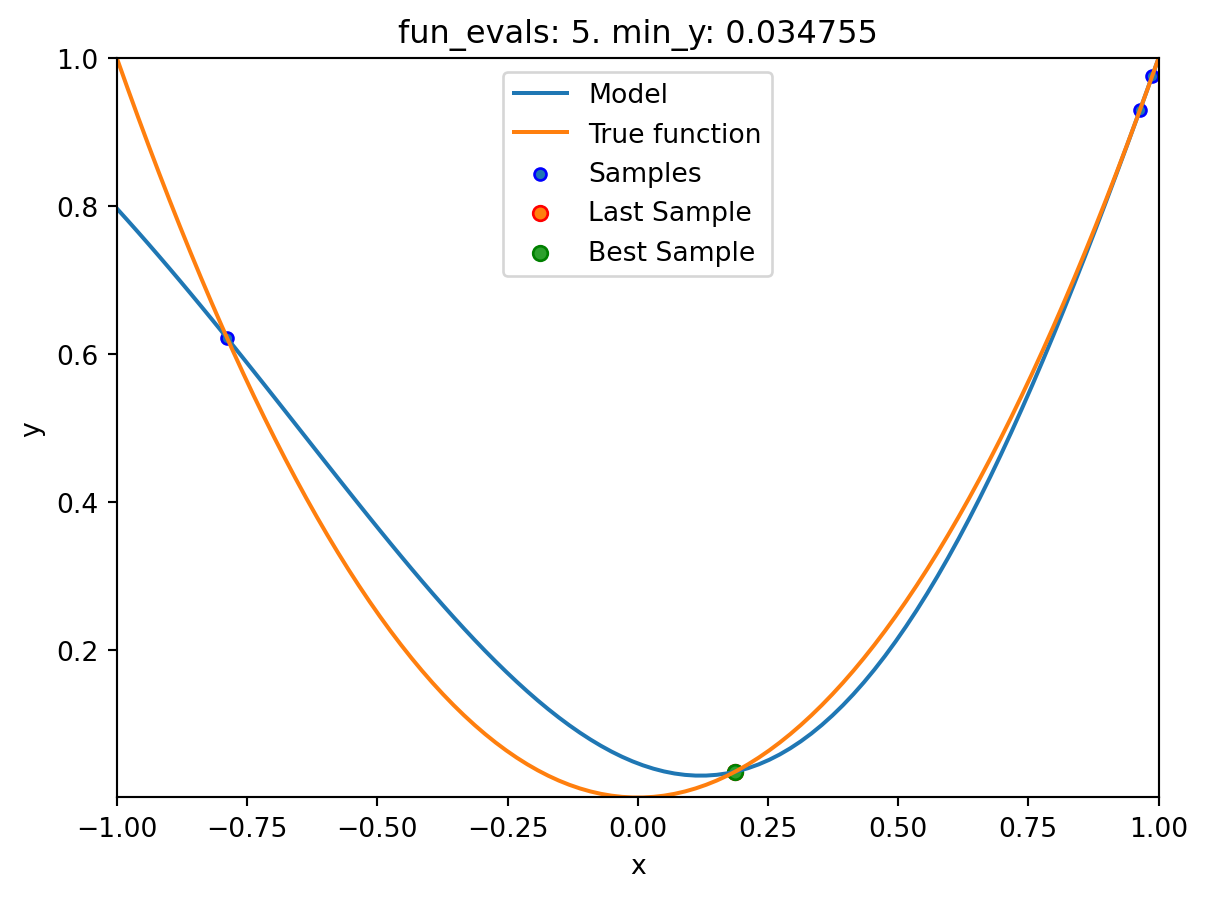 

spotpython tuning: 0.03475493366922229 [#####-----] 50.00%. Success rate: 0.00%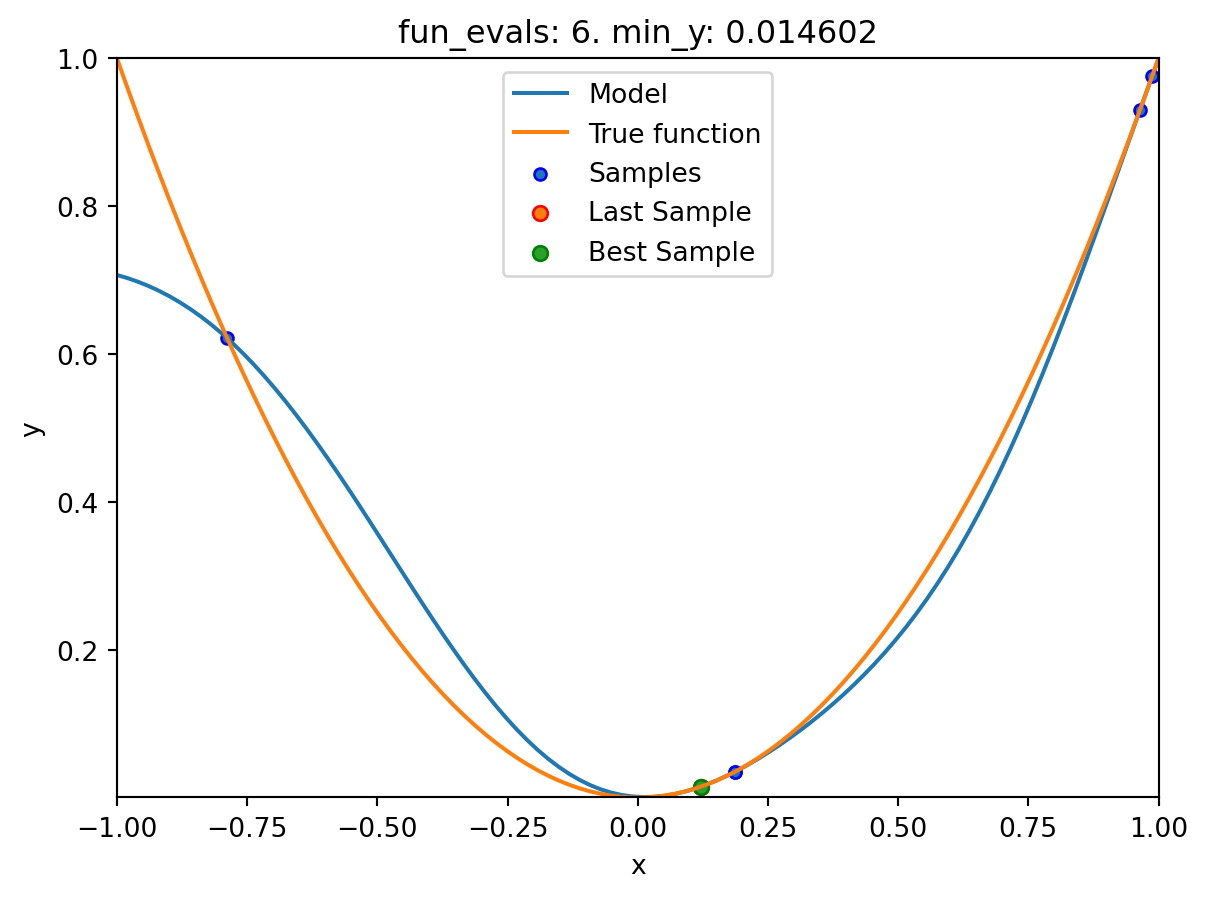 

spotpython tuning: 0.0002493578103496971 [######----] 60.00%. Success rate: 33.33%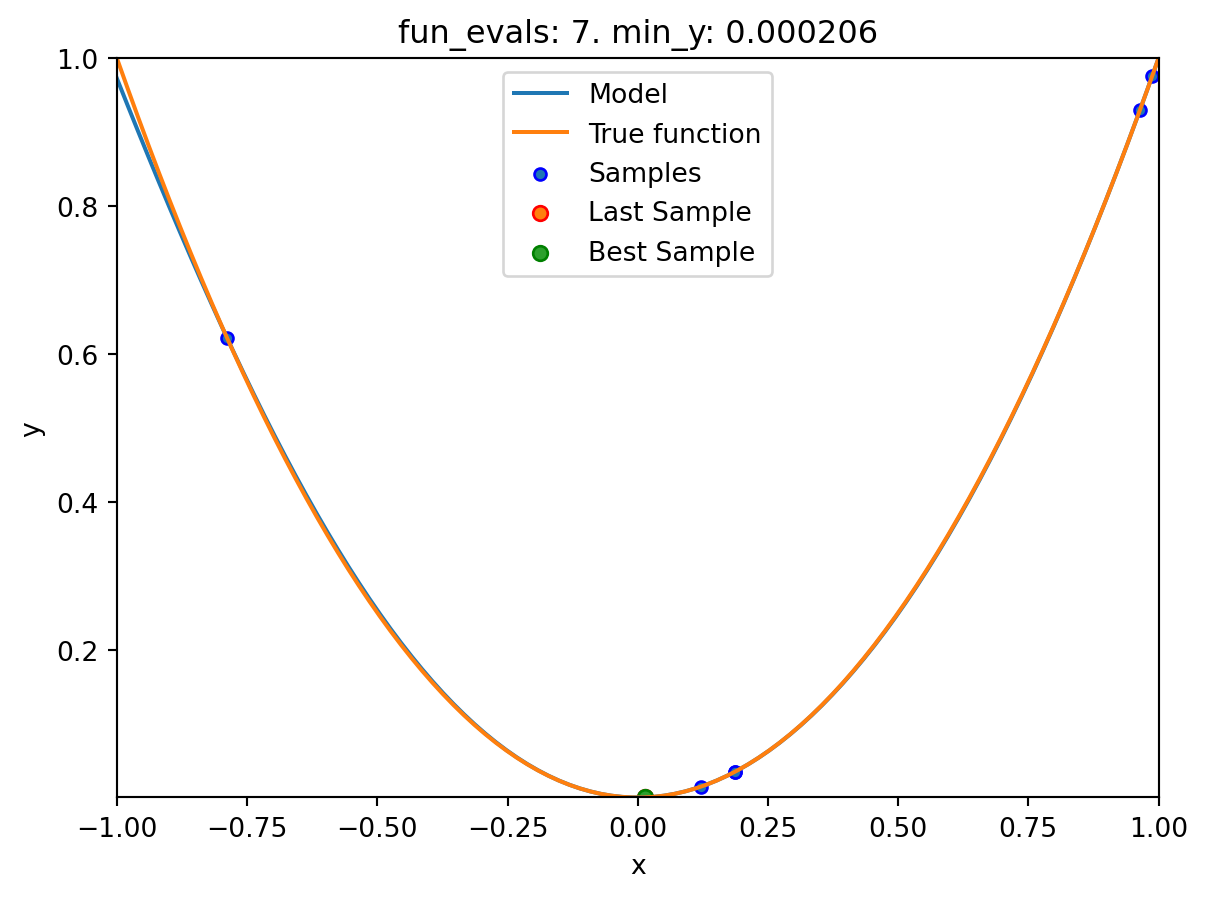 

spotpython tuning: 3.737005778245563e-07 [#######---] 70.00%. Success rate: 50.00%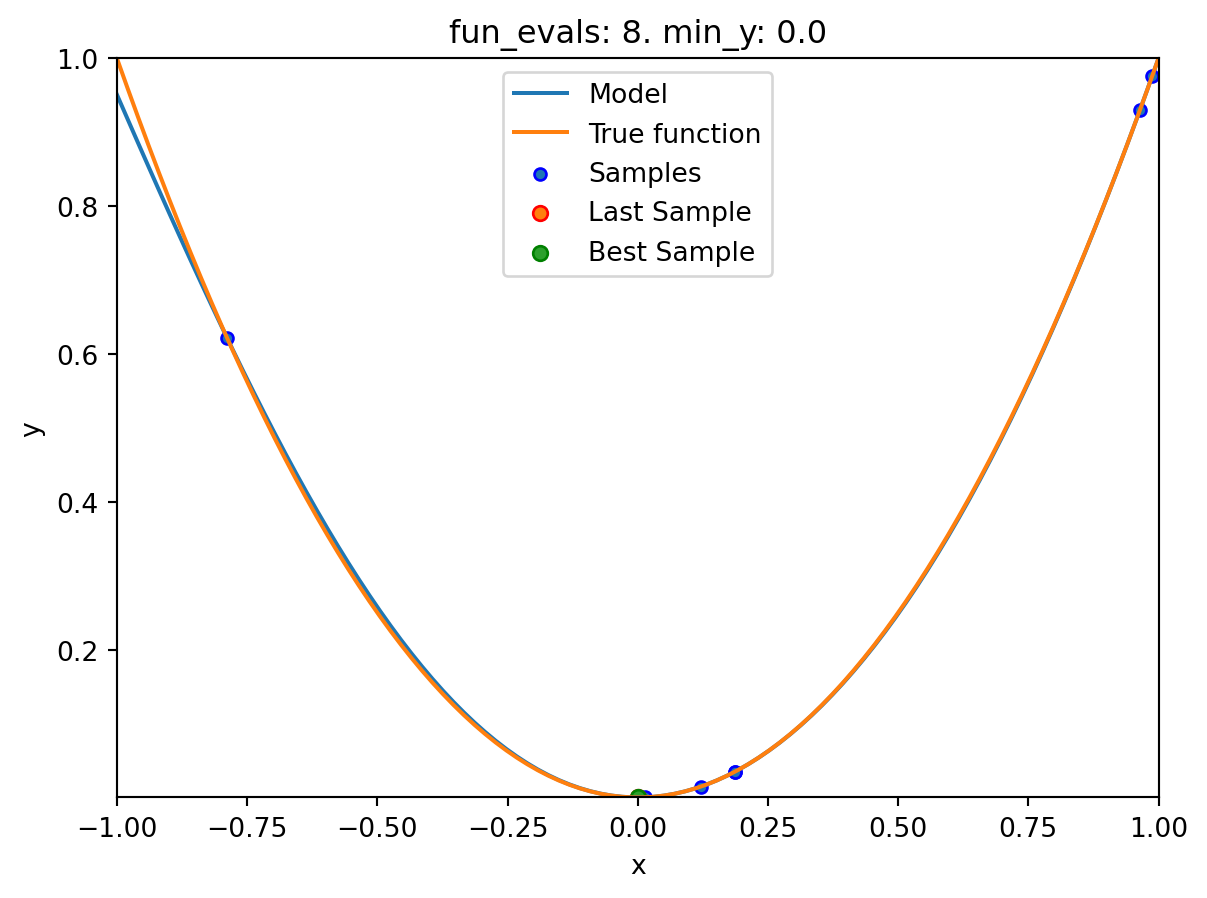 

spotpython tuning: 9.313071592223354e-08 [########--] 80.00%. Success rate: 60.00%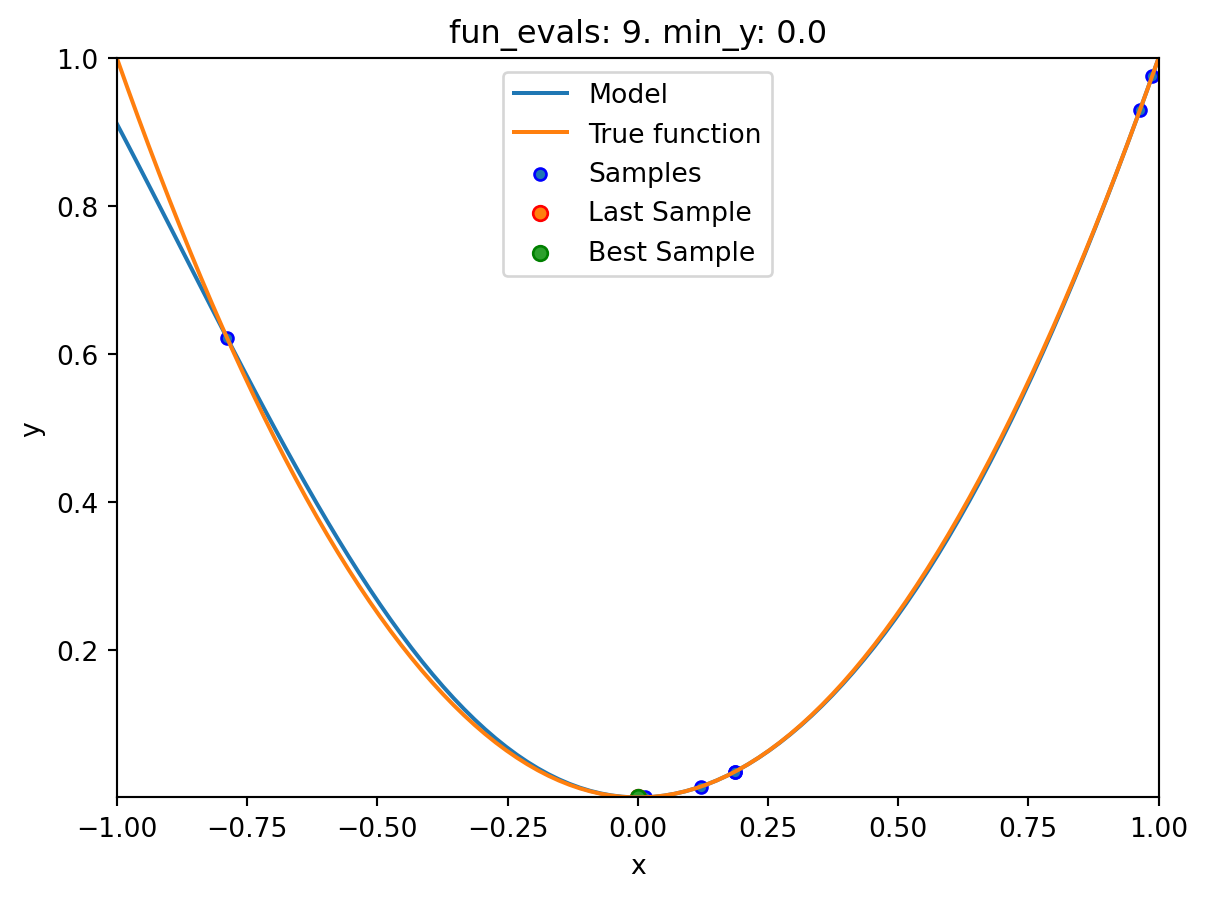 

spotpython tuning: 2.9997585469544003e-11 [#########-] 90.00%. Success rate: 66.67% 

spotpython tuning: 2.9997585469544003e-11 [##########] 100.00%. Success rate: 57.14% Done...

Experiment saved to 000_res.pkl
  • Print the Results
spot_1.print_results()
min y: 2.9997585469544003e-11
x0: -5.477005155150395e-06
[['x0', np.float64(-5.477005155150395e-06)]]
  • Show the Progress
spot_1.plot_progress(log_y=True)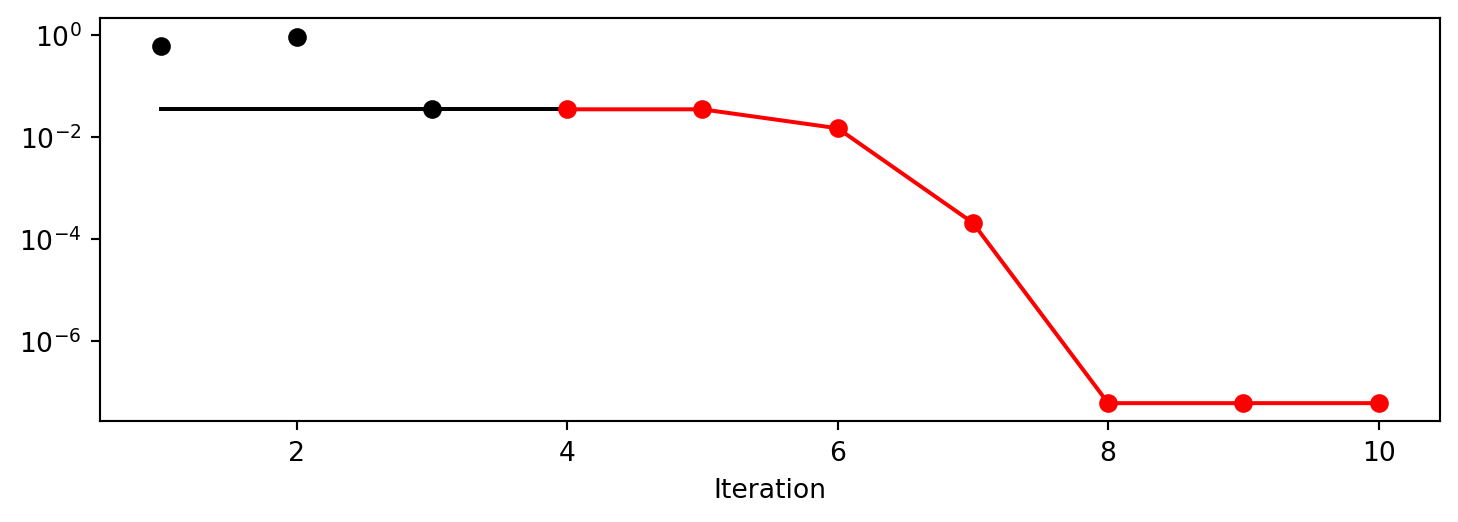

  • The method plot_model plots the final surrogate:
spot_1.plot_model()

16.6.1.4 One-dimensional Sphere Function With Sklearn Model HistGradientBoostingRegressor

  • This example visualizes the search process on the HistGradientBoostingRegressor surrogate from sklearn.
  • Therefore surrogate = S_XGB is added to the argument list.
fun_control = fun_control_init(
    lower = np.array([-1]),
    upper = np.array([1]),
    fun_evals=10,
    max_time=inf,
    show_models= True,
    tolerance_x = np.sqrt(np.spacing(1)))
fun = Analytical(seed=123).fun_sphere
design_control = design_control_init(
    init_size=3)
spot_1_XGB = Spot(fun=fun,
                      fun_control=fun_control,
                      design_control=design_control,
                      surrogate = S_XGB)
spot_1_XGB.run()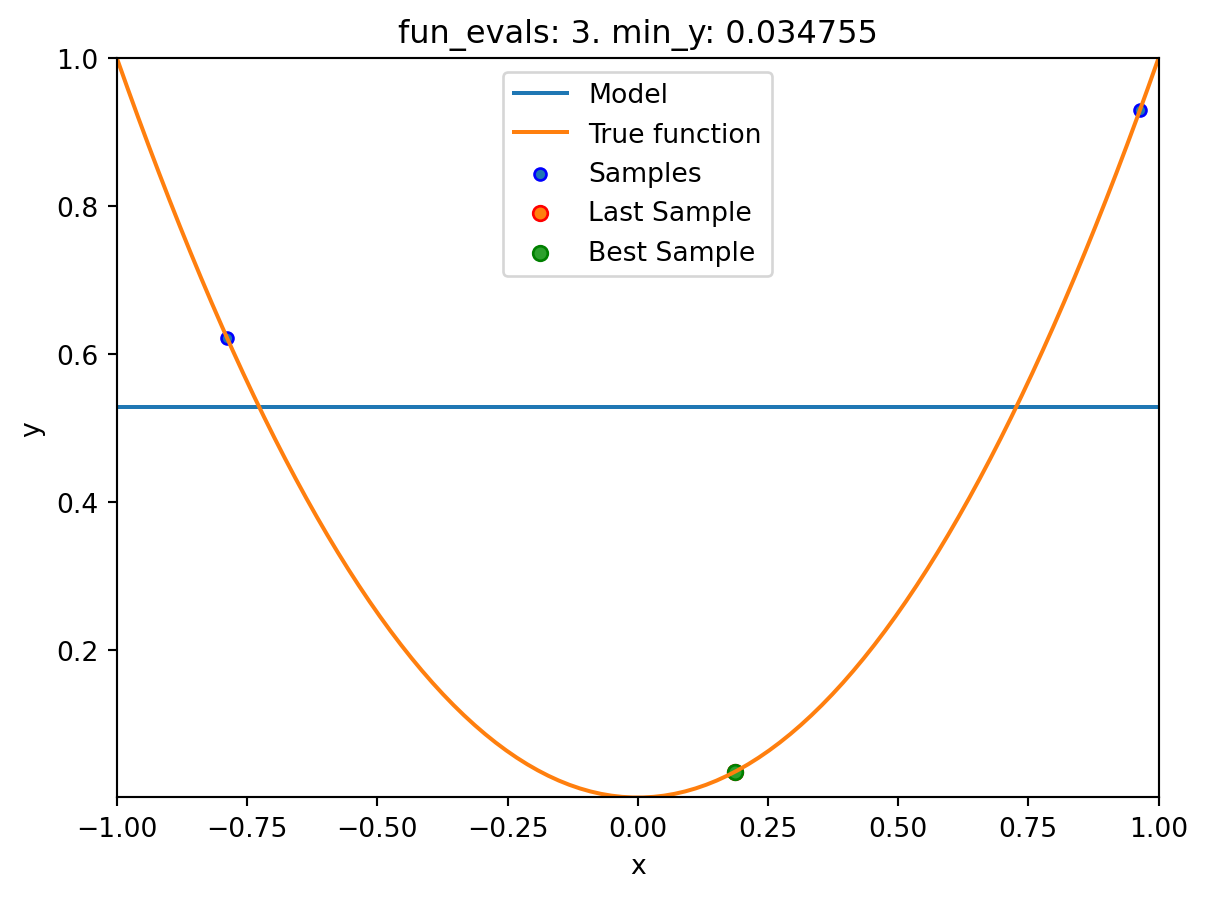

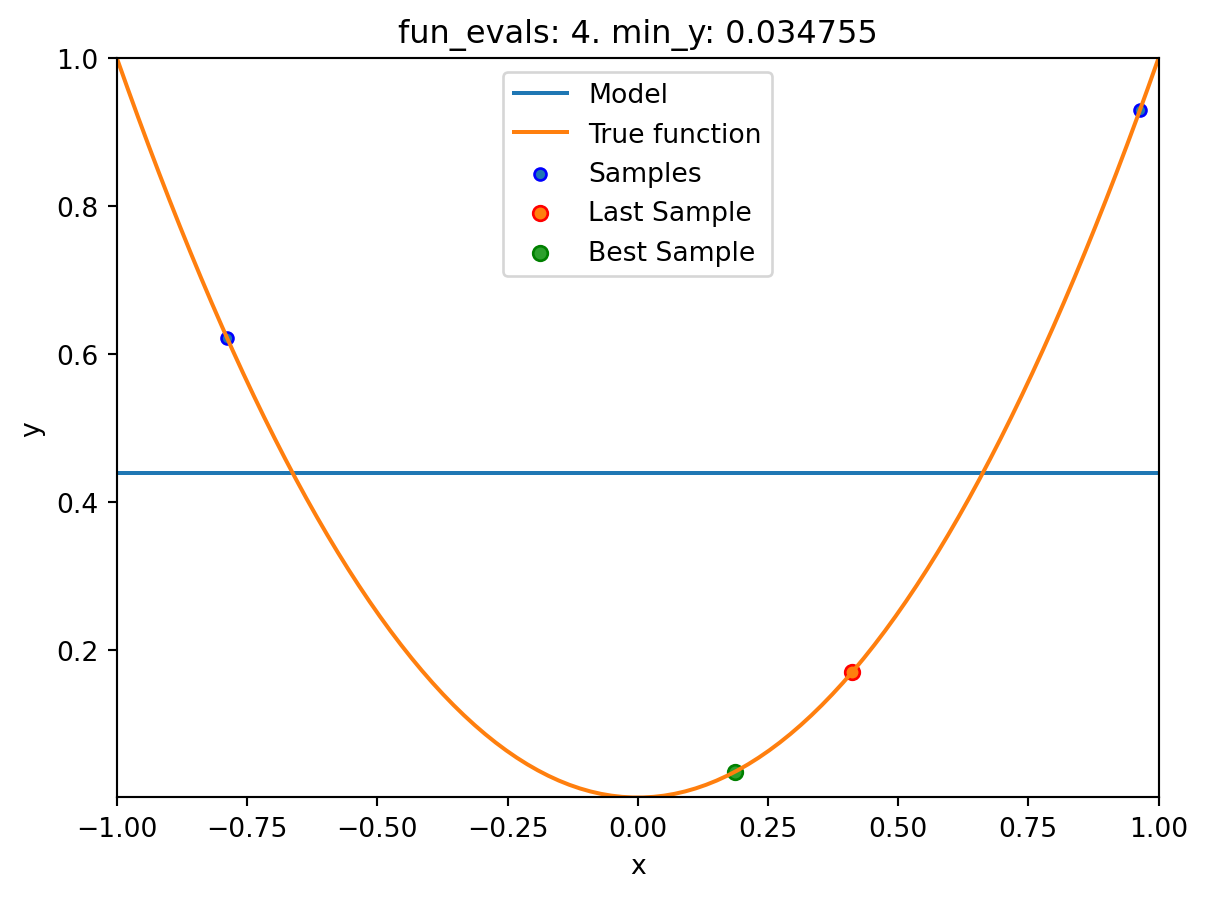
spotpython tuning: 0.03475493366922229 [####------] 40.00%. Success rate: 0.00% 
Using spacefilling design as fallback.

spotpython tuning: 0.03475493366922229 [#####-----] 50.00%. Success rate: 0.00% 
Using spacefilling design as fallback.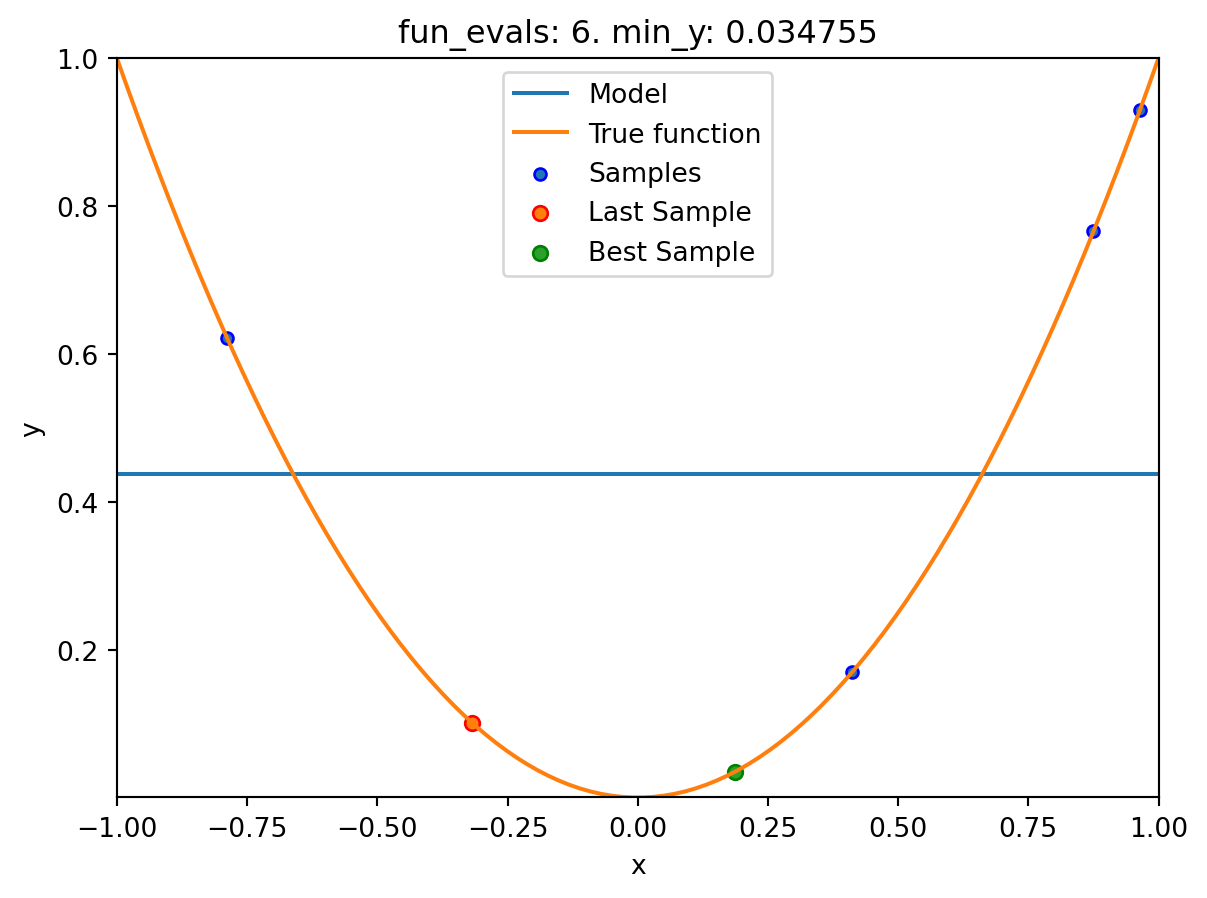

spotpython tuning: 0.03475493366922229 [######----] 60.00%. Success rate: 0.00% 
Using spacefilling design as fallback.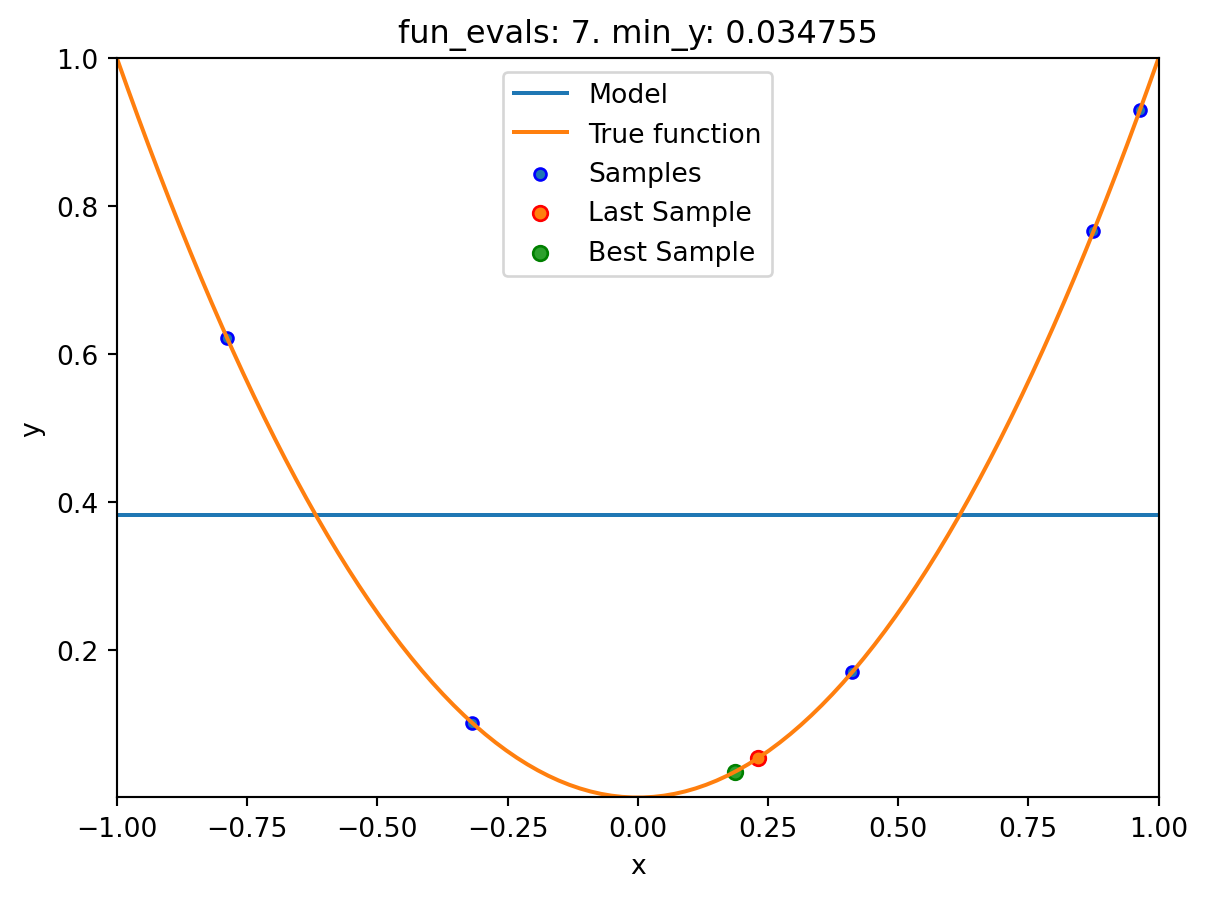

spotpython tuning: 0.03475493366922229 [#######---] 70.00%. Success rate: 0.00% 
Using spacefilling design as fallback.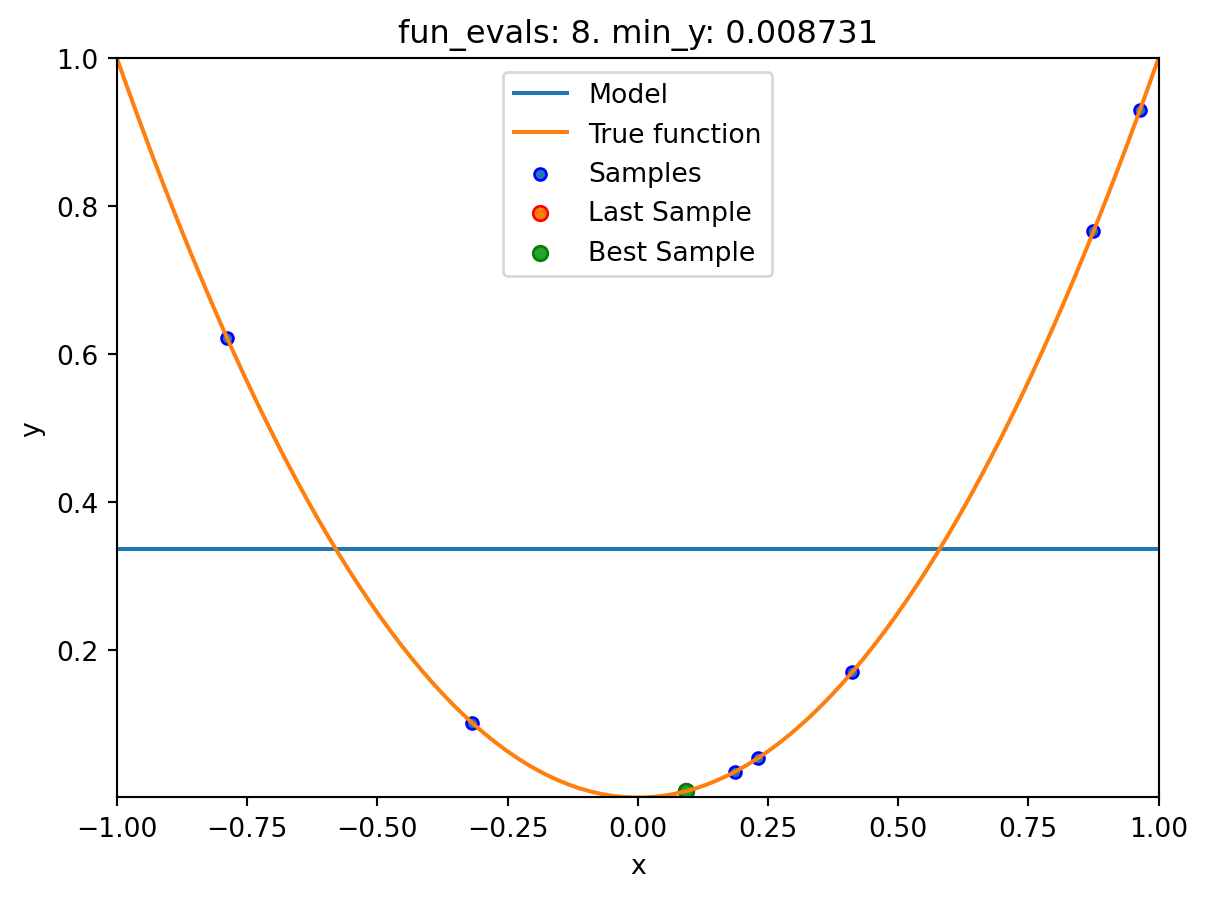

spotpython tuning: 0.008730885505764131 [########--] 80.00%. Success rate: 20.00% 
Using spacefilling design as fallback.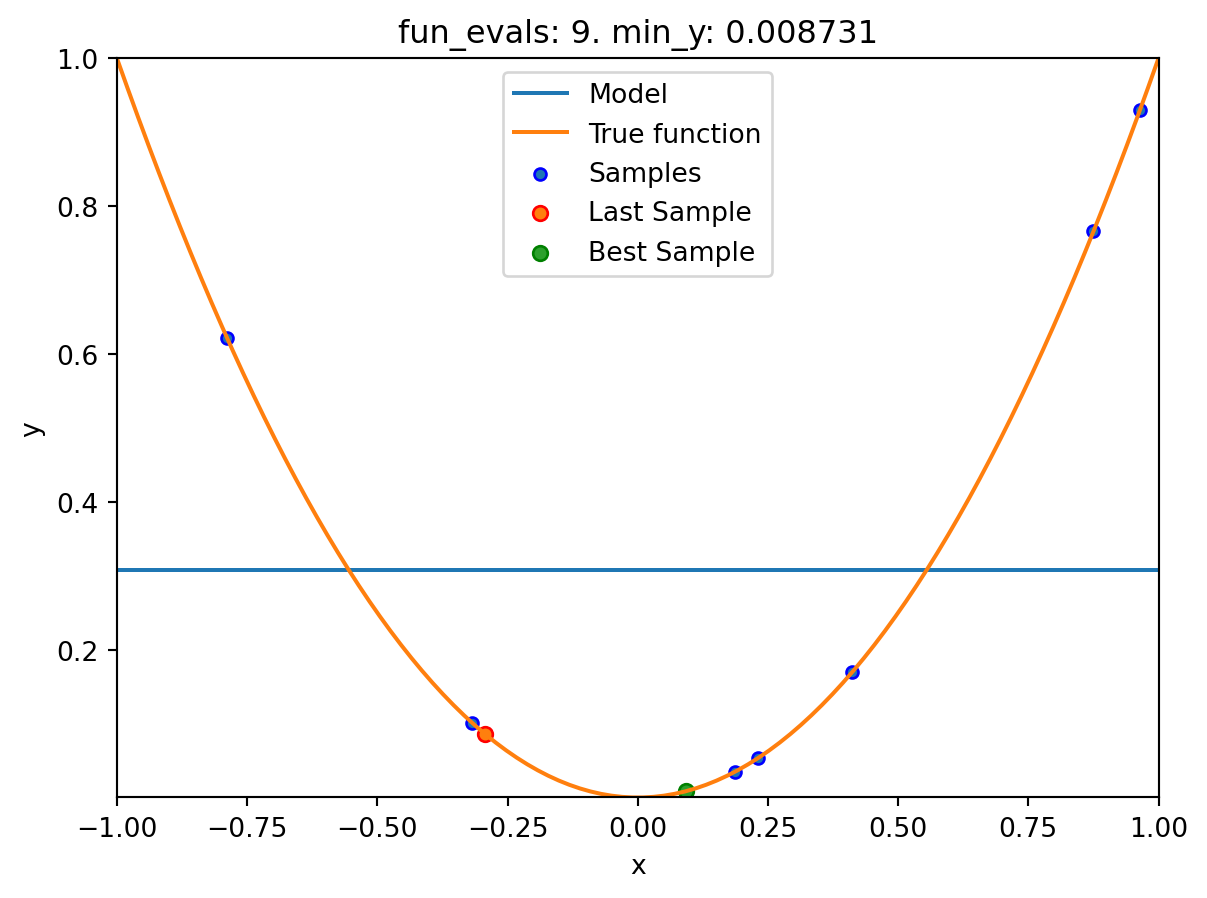

spotpython tuning: 0.008730885505764131 [#########-] 90.00%. Success rate: 16.67% 
Using spacefilling design as fallback.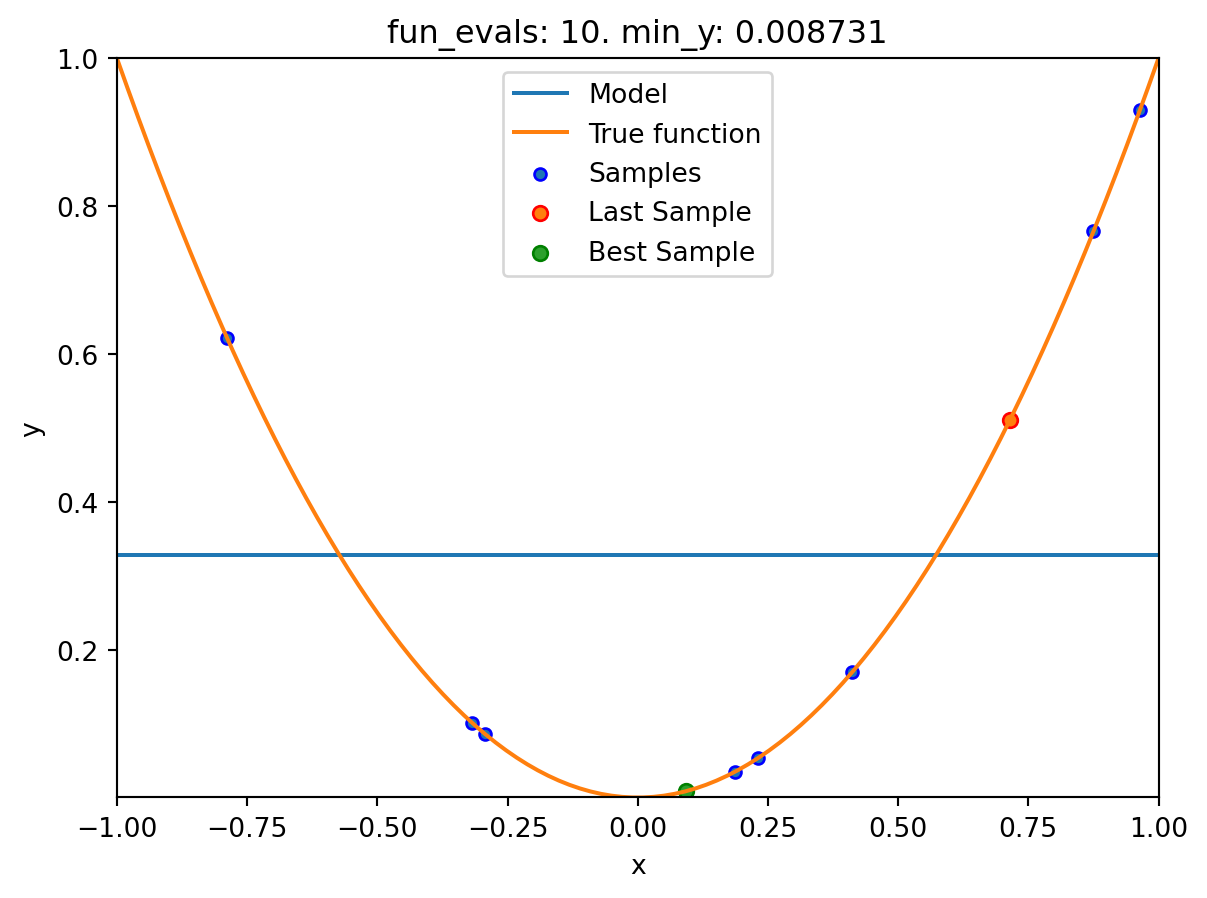

spotpython tuning: 0.008730885505764131 [##########] 100.00%. Success rate: 14.29% Done...

Experiment saved to 000_res.pkl
spot_1_XGB.print_results()
min y: 0.008730885505764131
x0: 0.09343920754032609
[['x0', np.float64(0.09343920754032609)]]
spot_1_XGB.plot_progress(log_y=True)

spot_1_XGB.plot_model()

16.7 Jupyter Notebook

Note