4 Sequential Parameter Optimization: Using `scipy` Optimizers

As a default optimizer, spotPython uses differential_evolution from the scipy.optimize package. Alternatively, any other optimizer from the scipy.optimize package can be used. This chapter describes how different optimizers from the scipy optimize package can be used on the surrogate. The optimization algorithms are available from https://docs.scipy.org/doc/scipy/reference/optimize.html

import numpy as np
from math import inf
from spotPython.fun.objectivefunctions import analytical
from spotPython.spot import spot
from scipy.optimize import shgo
from scipy.optimize import direct
from scipy.optimize import differential_evolution
from scipy.optimize import dual_annealing
from scipy.optimize import basinhopping
from spotPython.utils.init import fun_control_init, design_control_init, optimizer_control_init, surrogate_control_init

4.1 The Objective Function Branin

The spotPython package provides several classes of objective functions. We will use an analytical objective function, i.e., a function that can be described by a (closed) formula. Here we will use the Branin function. The 2-dim Branin function is

$$y = a * (x2 - b * x1**2 + c * x1 - r) ** 2 + s * (1 - t) * cos(x1) + s,$$ 
where values of a, b, c, r, s and t are: 
$a = 1, b = 5.1 / (4*pi**2), c = 5 / pi, r = 6, s = 10$ and $t = 1 / (8*pi)$.

It has three global minima:

\(f(x) = 0.397887\) at \((-\pi, 12.275)\), \((\pi, 2.275)\), and \((9.42478, 2.475)\).
Input Domain: This function is usually evaluated on the square x1 in [-5, 10] x x2 in [0, 15].

from spotPython.fun.objectivefunctions import analytical
lower = np.array([-5,-0])
upper = np.array([10,15])
fun = analytical(seed=123).fun_branin

4.2 The Optimizer

Differential Evolution (DE) from the scikit.optimize package, see https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html#scipy.optimize.differential_evolution is the default optimizer for the search on the surrogate. Other optimiers that are available in spotPython, see https://docs.scipy.org/doc/scipy/reference/optimize.html#global-optimization.

dual_annealing
direct
shgo
basinhopping

These optimizers can be selected as follows:

surrogate_control = "model_optimizer": differential_evolution

As noted above, we will use differential_evolution. The optimizer can use 1000 evaluations. This value will be passed to the differential_evolution method, which has the argument maxiter (int). It defines the maximum number of generations over which the entire differential evolution population is evolved, see https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.differential_evolution.html#scipy.optimize.differential_evolution

TensorBoard

Similar to the one-dimensional case, which is discussed in Section 7.5, we can use TensorBoard to monitor the progress of the optimization. We will use a similar code, only the prefix is different:

fun_control=fun_control_init(
                    lower = lower,
                    upper = upper,
                    fun_evals = 20,
                    PREFIX = "04_DE_"
                    )
surrogate_control=surrogate_control_init(
                    n_theta=len(lower))

Created spot_tensorboard_path: runs/spot_logs/04_DE__maans14_2024-04-22_00-18-10 for SummaryWriter()

spot_de = spot.Spot(fun=fun,
                    fun_control=fun_control,
                    surrogate_control=surrogate_control)
spot_de.run()

spotPython tuning: 3.8004644561334935 [######----] 55.00% 
spotPython tuning: 3.8004644561334935 [######----] 60.00% 
spotPython tuning: 3.1590379739505225 [######----] 65.00% 
spotPython tuning: 3.1345599589760926 [#######---] 70.00% 
spotPython tuning: 2.8987595919440583 [########--] 75.00% 
spotPython tuning: 0.4124604824941809 [########--] 80.00% 
spotPython tuning: 0.40391426855740775 [########--] 85.00% 
spotPython tuning: 0.3990718447916741 [#########-] 90.00% 
spotPython tuning: 0.3990718447916741 [##########] 95.00% 
spotPython tuning: 0.3990718447916741 [##########] 100.00% Done...

{'CHECKPOINT_PATH': 'runs/saved_models/',
 'DATASET_PATH': 'data/',
 'PREFIX': '04_DE_',
 'RESULTS_PATH': 'results/',
 'TENSORBOARD_PATH': 'runs/',
 '_L_in': None,
 '_L_out': None,
 '_torchmetric': None,
 'accelerator': 'auto',
 'converters': None,
 'core_model': None,
 'core_model_name': None,
 'counter': 20,
 'data': None,
 'data_dir': './data',
 'data_module': None,
 'data_set': None,
 'data_set_name': None,
 'db_dict_name': None,
 'design': None,
 'device': None,
 'devices': 1,
 'enable_progress_bar': False,
 'eval': None,
 'fun_evals': 20,
 'fun_repeats': 1,
 'horizon': None,
 'infill_criterion': 'y',
 'k_folds': 3,
 'log_graph': False,
 'log_level': 50,
 'loss_function': None,
 'lower': array([-5,  0]),
 'max_surrogate_points': 30,
 'max_time': 1,
 'metric_params': {},
 'metric_river': None,
 'metric_sklearn': None,
 'metric_sklearn_name': None,
 'metric_torch': None,
 'model_dict': {},
 'n_points': 1,
 'n_samples': None,
 'n_total': None,
 'noise': False,
 'num_workers': 0,
 'ocba_delta': 0,
 'oml_grace_period': None,
 'optimizer': None,
 'path': None,
 'prep_model': None,
 'prep_model_name': None,
 'progress_file': None,
 'save_model': False,
 'scenario': None,
 'seed': 123,
 'show_batch_interval': 1000000,
 'show_models': False,
 'show_progress': True,
 'shuffle': None,
 'sigma': 0.0,
 'spot_tensorboard_path': 'runs/spot_logs/04_DE__maans14_2024-04-22_00-18-10',
 'spot_writer': <torch.utils.tensorboard.writer.SummaryWriter object at 0x3c86e6f50>,
 'target_column': None,
 'target_type': None,
 'task': None,
 'test': None,
 'test_seed': 1234,
 'test_size': 0.4,
 'tolerance_x': 0,
 'train': None,
 'upper': array([10, 15]),
 'var_name': None,
 'var_type': ['num'],
 'verbosity': 0,
 'weight_coeff': 0.0,
 'weights': 1.0,
 'weights_entry': None}

<spotPython.spot.spot.Spot at 0x3c94c8090>

4.2.1 TensorBoard

If the prefix argument in fun_control_init()is not None (as above, where the prefix was set to 04_DE_) , we can start TensorBoard in the background with the following command:

tensorboard --logdir="./runs"

We can access the TensorBoard web server with the following URL:

http://localhost:6006/

The TensorBoard plot illustrates how spotPython can be used as a microscope for the internal mechanisms of the surrogate-based optimization process. Here, one important parameter, the learning rate \(\theta\) of the Kriging surrogate is plotted against the number of optimization steps.

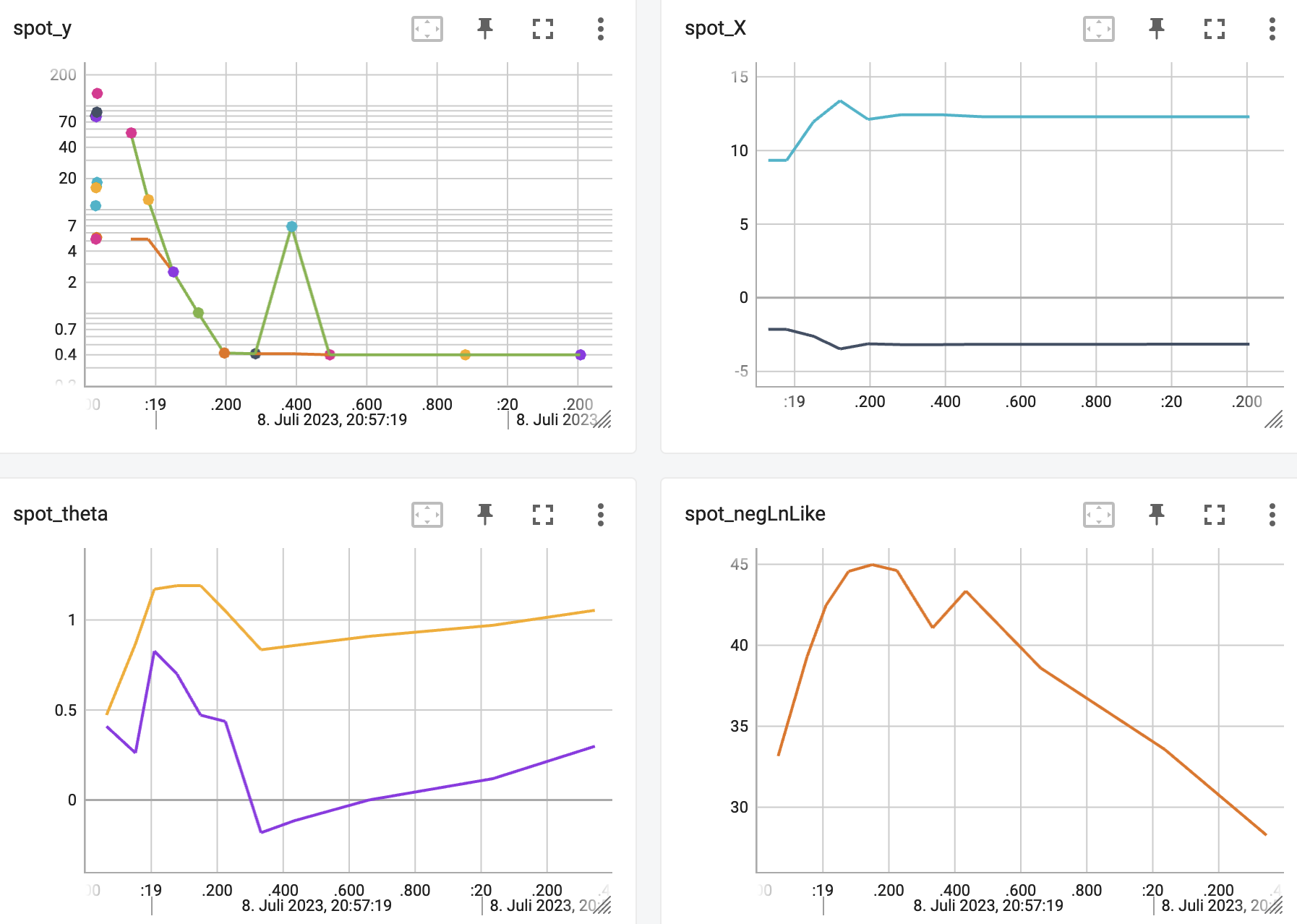
TensorBoard visualization of the spotPython optimization process and the surrogate model.

4.3 Print the Results

spot_de.print_results()

min y: 0.3990718447916741
x0: 3.149600915888656
x1: 2.2983701643039107

[['x0', 3.149600915888656], ['x1', 2.2983701643039107]]

4.4 Show the Progress

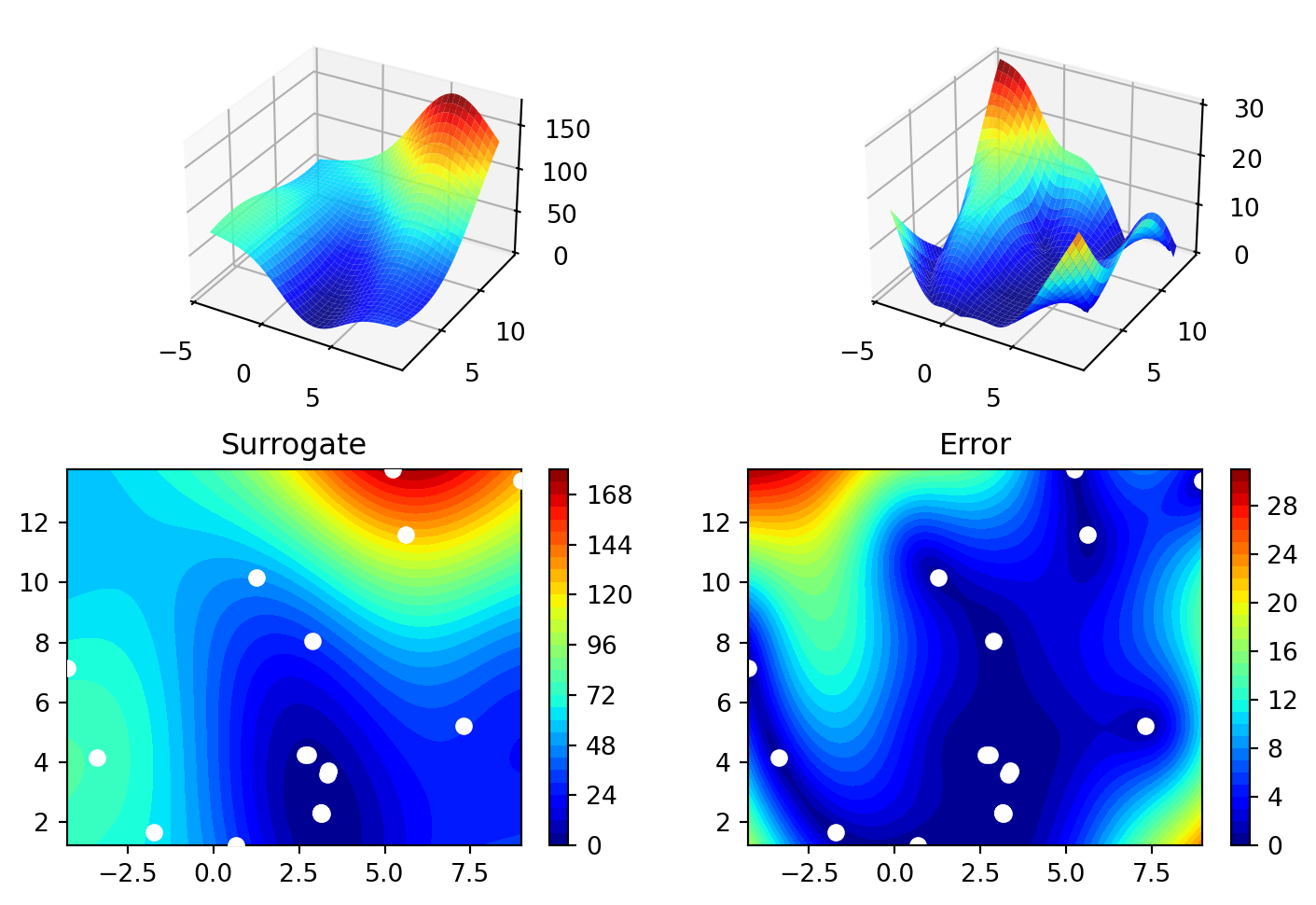
spot_de.plot_progress(log_y=True)

spot_de.surrogate.plot()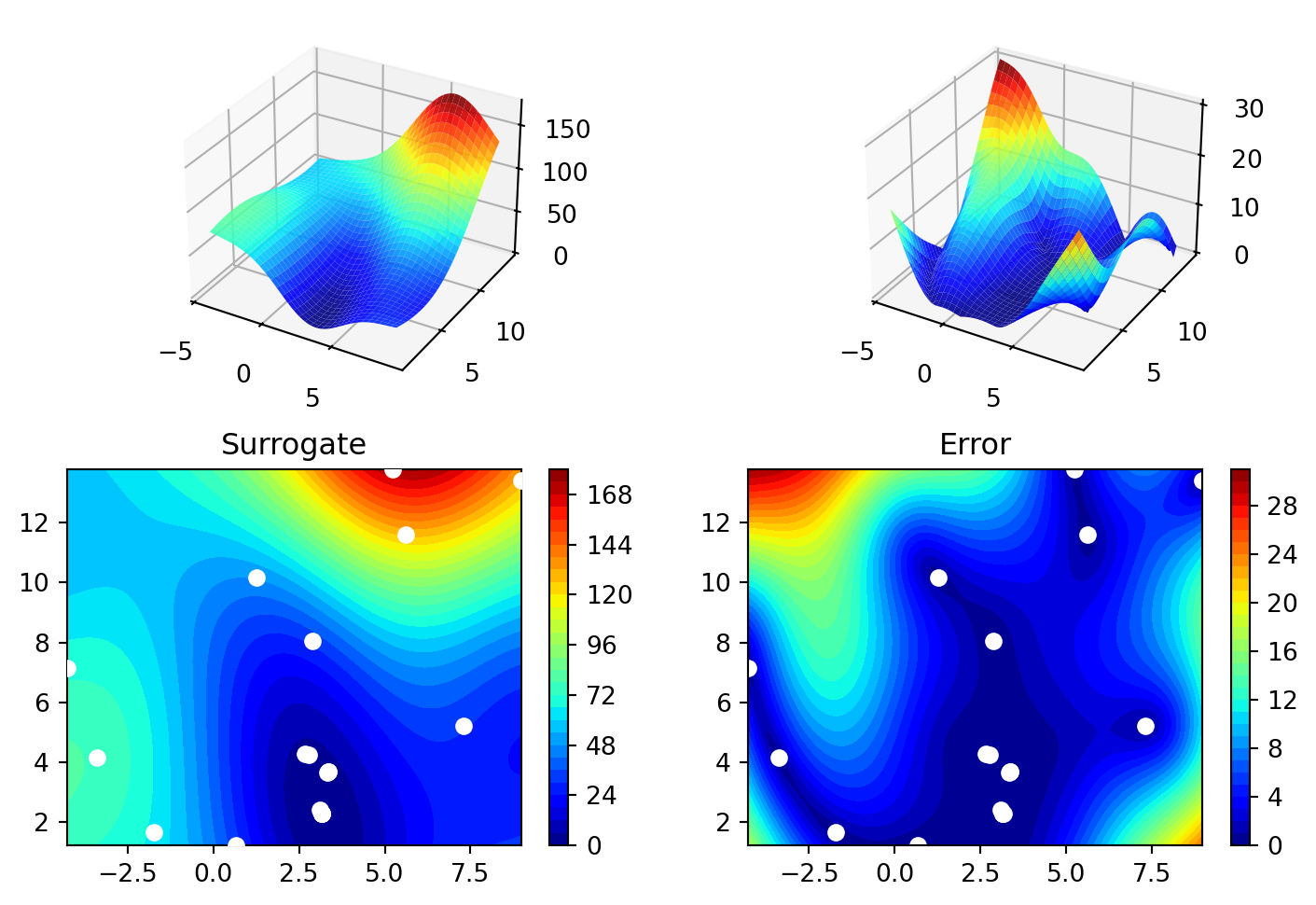

4.5 Exercises

4.5.1 `dual_annealing`

Describe the optimization algorithm, see scipy.optimize.dual_annealing.
Use the algorithm as an optimizer on the surrogate.

Tip: Selecting the Optimizer for the Surrogate

We can run spotPython with the dual_annealing optimizer as follows:

spot_da = spot.Spot(fun=fun,
                    fun_control=fun_control,
                    optimizer=dual_annealing,
                    surrogate_control=surrogate_control)
spot_da.run()
spot_da.print_results()
spot_da.plot_progress(log_y=True)
spot_da.surrogate.plot()

spotPython tuning: 3.800452934057194 [######----] 55.00% 
spotPython tuning: 3.800452934057194 [######----] 60.00% 
spotPython tuning: 3.1590242778566413 [######----] 65.00% 
spotPython tuning: 3.1341475332648105 [#######---] 70.00% 
spotPython tuning: 2.8915909597236436 [########--] 75.00% 
spotPython tuning: 0.4195069442130439 [########--] 80.00% 
spotPython tuning: 0.401848680281649 [########--] 85.00% 
spotPython tuning: 0.3992571870039132 [#########-] 90.00% 
spotPython tuning: 0.3992571870039132 [##########] 95.00% 
spotPython tuning: 0.3992571870039132 [##########] 100.00% Done...

{'CHECKPOINT_PATH': 'runs/saved_models/',
 'DATASET_PATH': 'data/',
 'PREFIX': '04_DE_',
 'RESULTS_PATH': 'results/',
 'TENSORBOARD_PATH': 'runs/',
 '_L_in': None,
 '_L_out': None,
 '_torchmetric': None,
 'accelerator': 'auto',
 'converters': None,
 'core_model': None,
 'core_model_name': None,
 'counter': 20,
 'data': None,
 'data_dir': './data',
 'data_module': None,
 'data_set': None,
 'data_set_name': None,
 'db_dict_name': None,
 'design': None,
 'device': None,
 'devices': 1,
 'enable_progress_bar': False,
 'eval': None,
 'fun_evals': 20,
 'fun_repeats': 1,
 'horizon': None,
 'infill_criterion': 'y',
 'k_folds': 3,
 'log_graph': False,
 'log_level': 50,
 'loss_function': None,
 'lower': array([-5,  0]),
 'max_surrogate_points': 30,
 'max_time': 1,
 'metric_params': {},
 'metric_river': None,
 'metric_sklearn': None,
 'metric_sklearn_name': None,
 'metric_torch': None,
 'model_dict': {},
 'n_points': 1,
 'n_samples': None,
 'n_total': None,
 'noise': False,
 'num_workers': 0,
 'ocba_delta': 0,
 'oml_grace_period': None,
 'optimizer': None,
 'path': None,
 'prep_model': None,
 'prep_model_name': None,
 'progress_file': None,
 'save_model': False,
 'scenario': None,
 'seed': 123,
 'show_batch_interval': 1000000,
 'show_models': False,
 'show_progress': True,
 'shuffle': None,
 'sigma': 0.0,
 'spot_tensorboard_path': 'runs/spot_logs/04_DE__maans14_2024-04-22_00-18-10',
 'spot_writer': <torch.utils.tensorboard.writer.SummaryWriter object at 0x3c86e6f50>,
 'target_column': None,
 'target_type': None,
 'task': None,
 'test': None,
 'test_seed': 1234,
 'test_size': 0.4,
 'tolerance_x': 0,
 'train': None,
 'upper': array([10, 15]),
 'var_name': None,
 'var_type': ['num'],
 'verbosity': 0,
 'weight_coeff': 0.0,
 'weights': 1.0,
 'weights_entry': None}
min y: 0.3992571870039132
x0: 3.150936988317143
x1: 2.2985561477641263

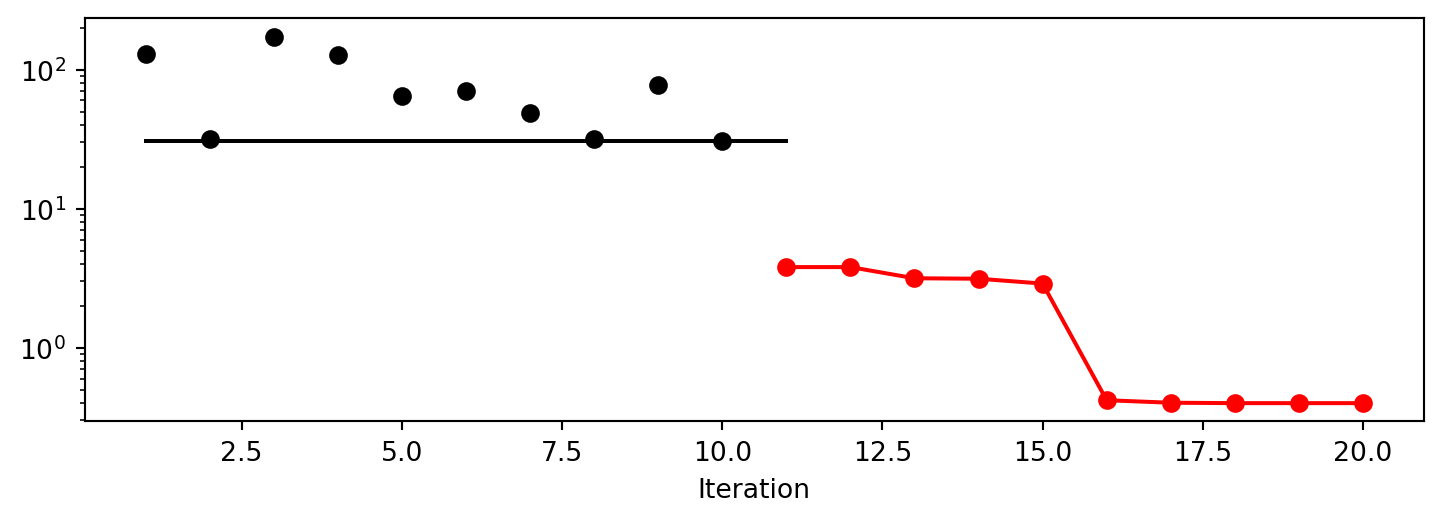
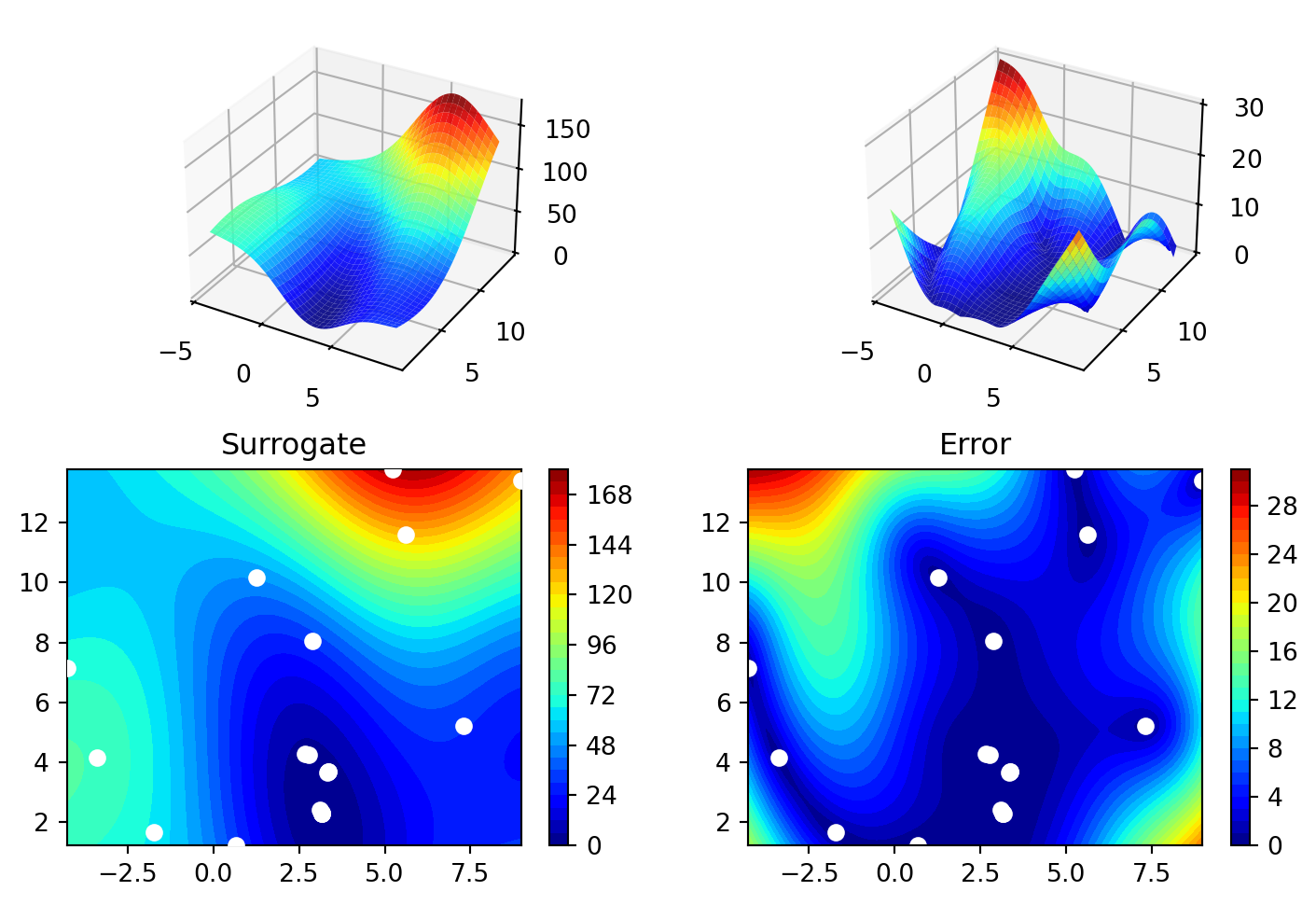
4.5.2 `direct`

Describe the optimization algorithm
Use the algorithm as an optimizer on the surrogate

Tip: Selecting the Optimizer for the Surrogate

We can run spotPython with the direct optimizer as follows:

spot_di = spot.Spot(fun=fun,
                    fun_control=fun_control,
                    optimizer=direct,
                    surrogate_control=surrogate_control)
spot_di.run()
spot_di.print_results()
spot_di.plot_progress(log_y=True)
spot_di.surrogate.plot()

spotPython tuning: 3.812970247994418 [######----] 55.00% 
spotPython tuning: 3.812970247994418 [######----] 60.00% 
spotPython tuning: 3.162514679816068 [######----] 65.00% 
spotPython tuning: 3.1189615135325983 [#######---] 70.00% 
spotPython tuning: 2.6597698275013 [########--] 75.00% 
spotPython tuning: 0.3984917773445744 [########--] 80.00% 
spotPython tuning: 0.3984917773445744 [########--] 85.00% 
spotPython tuning: 0.3984917773445744 [#########-] 90.00% 
spotPython tuning: 0.3984917773445744 [##########] 95.00% 
spotPython tuning: 0.3984917773445744 [##########] 100.00% Done...

{'CHECKPOINT_PATH': 'runs/saved_models/',
 'DATASET_PATH': 'data/',
 'PREFIX': '04_DE_',
 'RESULTS_PATH': 'results/',
 'TENSORBOARD_PATH': 'runs/',
 '_L_in': None,
 '_L_out': None,
 '_torchmetric': None,
 'accelerator': 'auto',
 'converters': None,
 'core_model': None,
 'core_model_name': None,
 'counter': 20,
 'data': None,
 'data_dir': './data',
 'data_module': None,
 'data_set': None,
 'data_set_name': None,
 'db_dict_name': None,
 'design': None,
 'device': None,
 'devices': 1,
 'enable_progress_bar': False,
 'eval': None,
 'fun_evals': 20,
 'fun_repeats': 1,
 'horizon': None,
 'infill_criterion': 'y',
 'k_folds': 3,
 'log_graph': False,
 'log_level': 50,
 'loss_function': None,
 'lower': array([-5,  0]),
 'max_surrogate_points': 30,
 'max_time': 1,
 'metric_params': {},
 'metric_river': None,
 'metric_sklearn': None,
 'metric_sklearn_name': None,
 'metric_torch': None,
 'model_dict': {},
 'n_points': 1,
 'n_samples': None,
 'n_total': None,
 'noise': False,
 'num_workers': 0,
 'ocba_delta': 0,
 'oml_grace_period': None,
 'optimizer': None,
 'path': None,
 'prep_model': None,
 'prep_model_name': None,
 'progress_file': None,
 'save_model': False,
 'scenario': None,
 'seed': 123,
 'show_batch_interval': 1000000,
 'show_models': False,
 'show_progress': True,
 'shuffle': None,
 'sigma': 0.0,
 'spot_tensorboard_path': 'runs/spot_logs/04_DE__maans14_2024-04-22_00-18-10',
 'spot_writer': <torch.utils.tensorboard.writer.SummaryWriter object at 0x3c86e6f50>,
 'target_column': None,
 'target_type': None,
 'task': None,
 'test': None,
 'test_seed': 1234,
 'test_size': 0.4,
 'tolerance_x': 0,
 'train': None,
 'upper': array([10, 15]),
 'var_name': None,
 'var_type': ['num'],
 'verbosity': 0,
 'weight_coeff': 0.0,
 'weights': 1.0,
 'weights_entry': None}
min y: 0.3984917773445744
x0: 3.1378600823045257
x1: 2.3010973936899863

4.5.3 `shgo`

Describe the optimization algorithm
Use the algorithm as an optimizer on the surrogate

Tip: Selecting the Optimizer for the Surrogate

We can run spotPython with the direct optimizer as follows:

spot_sh = spot.Spot(fun=fun,
                    fun_control=fun_control,
                    optimizer=shgo,
                    surrogate_control=surrogate_control)
spot_sh.run()
spot_sh.print_results()
spot_sh.plot_progress(log_y=True)
spot_sh.surrogate.plot()

spotPython tuning: 3.8004552384813834 [######----] 55.00% 
spotPython tuning: 3.8004552384813834 [######----] 60.00% 
spotPython tuning: 3.1590504084857294 [######----] 65.00% 
spotPython tuning: 3.1341080537914 [#######---] 70.00% 
spotPython tuning: 2.8853849830561646 [########--] 75.00% 
spotPython tuning: 0.4239413355798014 [########--] 80.00% 
spotPython tuning: 0.4016765366794104 [########--] 85.00% 
spotPython tuning: 0.3993233052368623 [#########-] 90.00% 
spotPython tuning: 0.3993233052368623 [##########] 95.00% 
spotPython tuning: 0.3993233052368623 [##########] 100.00% Done...

{'CHECKPOINT_PATH': 'runs/saved_models/',
 'DATASET_PATH': 'data/',
 'PREFIX': '04_DE_',
 'RESULTS_PATH': 'results/',
 'TENSORBOARD_PATH': 'runs/',
 '_L_in': None,
 '_L_out': None,
 '_torchmetric': None,
 'accelerator': 'auto',
 'converters': None,
 'core_model': None,
 'core_model_name': None,
 'counter': 20,
 'data': None,
 'data_dir': './data',
 'data_module': None,
 'data_set': None,
 'data_set_name': None,
 'db_dict_name': None,
 'design': None,
 'device': None,
 'devices': 1,
 'enable_progress_bar': False,
 'eval': None,
 'fun_evals': 20,
 'fun_repeats': 1,
 'horizon': None,
 'infill_criterion': 'y',
 'k_folds': 3,
 'log_graph': False,
 'log_level': 50,
 'loss_function': None,
 'lower': array([-5,  0]),
 'max_surrogate_points': 30,
 'max_time': 1,
 'metric_params': {},
 'metric_river': None,
 'metric_sklearn': None,
 'metric_sklearn_name': None,
 'metric_torch': None,
 'model_dict': {},
 'n_points': 1,
 'n_samples': None,
 'n_total': None,
 'noise': False,
 'num_workers': 0,
 'ocba_delta': 0,
 'oml_grace_period': None,
 'optimizer': None,
 'path': None,
 'prep_model': None,
 'prep_model_name': None,
 'progress_file': None,
 'save_model': False,
 'scenario': None,
 'seed': 123,
 'show_batch_interval': 1000000,
 'show_models': False,
 'show_progress': True,
 'shuffle': None,
 'sigma': 0.0,
 'spot_tensorboard_path': 'runs/spot_logs/04_DE__maans14_2024-04-22_00-18-10',
 'spot_writer': <torch.utils.tensorboard.writer.SummaryWriter object at 0x3c86e6f50>,
 'target_column': None,
 'target_type': None,
 'task': None,
 'test': None,
 'test_seed': 1234,
 'test_size': 0.4,
 'tolerance_x': 0,
 'train': None,
 'upper': array([10, 15]),
 'var_name': None,
 'var_type': ['num'],
 'verbosity': 0,
 'weight_coeff': 0.0,
 'weights': 1.0,
 'weights_entry': None}
min y: 0.3993233052368623
x0: 3.1514683455618786
x1: 2.2984189502295536

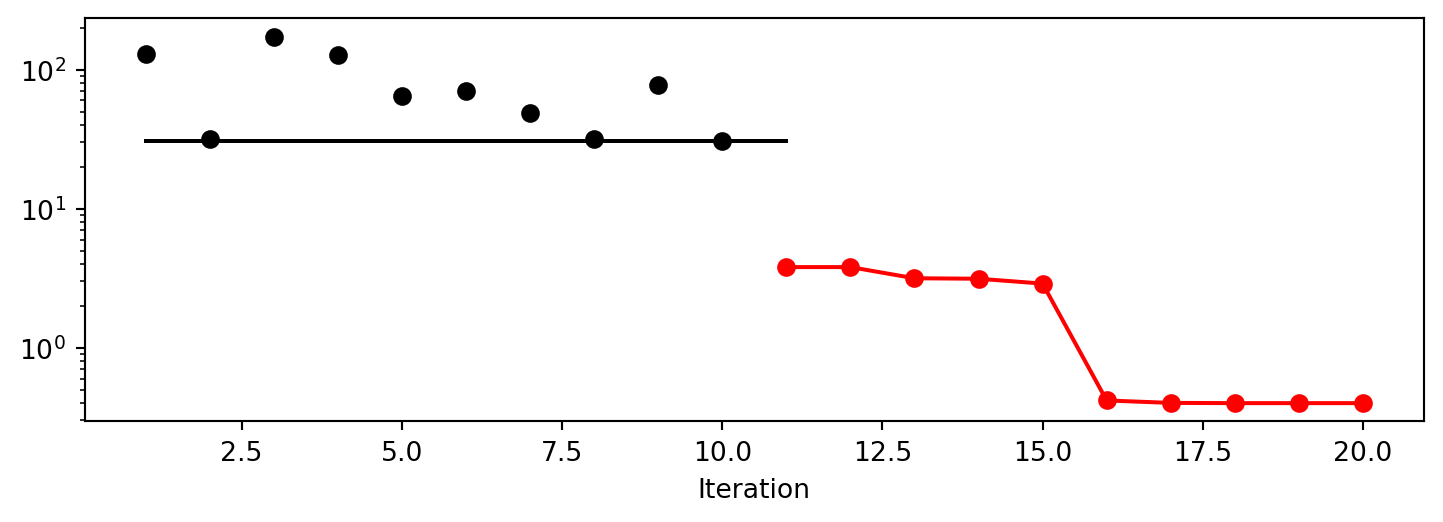
4.5.4 `basinhopping`

Describe the optimization algorithm
Use the algorithm as an optimizer on the surrogate

Tip: Selecting the Optimizer for the Surrogate

We can run spotPython with the direct optimizer as follows:

spot_bh = spot.Spot(fun=fun,
                    fun_control=fun_control,
                    optimizer=basinhopping,
                    surrogate_control=surrogate_control)
spot_bh.run()
spot_bh.print_results()
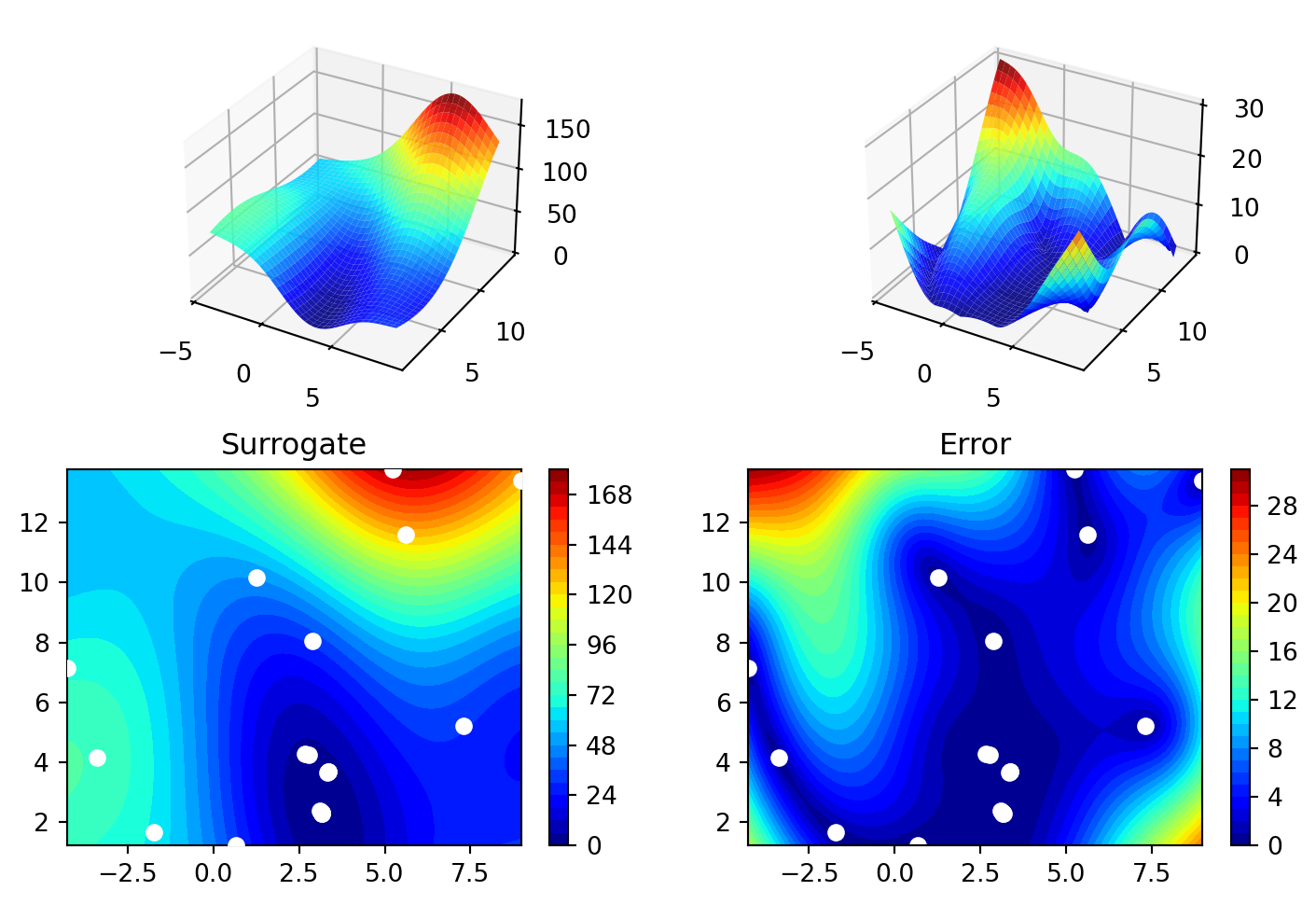
spot_bh.plot_progress(log_y=True)
spot_bh.surrogate.plot()

spotPython tuning: 3.80045375093536 [######----] 55.00% 
spotPython tuning: 3.80045375093536 [######----] 60.00% 
spotPython tuning: 3.159009257538889 [######----] 65.00% 
spotPython tuning: 3.1341512916720102 [#######---] 70.00% 
spotPython tuning: 2.8796407604155867 [########--] 75.00% 
spotPython tuning: 0.414633458827506 [########--] 80.00% 
spotPython tuning: 0.40117926479755717 [########--] 85.00% 
spotPython tuning: 0.3993792812618935 [#########-] 90.00% 
spotPython tuning: 0.3993792812618935 [##########] 95.00% 
spotPython tuning: 0.3993792812618935 [##########] 100.00% Done...

{'CHECKPOINT_PATH': 'runs/saved_models/',
 'DATASET_PATH': 'data/',
 'PREFIX': '04_DE_',
 'RESULTS_PATH': 'results/',
 'TENSORBOARD_PATH': 'runs/',
 '_L_in': None,
 '_L_out': None,
 '_torchmetric': None,
 'accelerator': 'auto',
 'converters': None,
 'core_model': None,
 'core_model_name': None,
 'counter': 20,
 'data': None,
 'data_dir': './data',
 'data_module': None,
 'data_set': None,
 'data_set_name': None,
 'db_dict_name': None,
 'design': None,
 'device': None,
 'devices': 1,
 'enable_progress_bar': False,
 'eval': None,
 'fun_evals': 20,
 'fun_repeats': 1,
 'horizon': None,
 'infill_criterion': 'y',
 'k_folds': 3,
 'log_graph': False,
 'log_level': 50,
 'loss_function': None,
 'lower': array([-5,  0]),
 'max_surrogate_points': 30,
 'max_time': 1,
 'metric_params': {},
 'metric_river': None,
 'metric_sklearn': None,
 'metric_sklearn_name': None,
 'metric_torch': None,
 'model_dict': {},
 'n_points': 1,
 'n_samples': None,
 'n_total': None,
 'noise': False,
 'num_workers': 0,
 'ocba_delta': 0,
 'oml_grace_period': None,
 'optimizer': None,
 'path': None,
 'prep_model': None,
 'prep_model_name': None,
 'progress_file': None,
 'save_model': False,
 'scenario': None,
 'seed': 123,
 'show_batch_interval': 1000000,
 'show_models': False,
 'show_progress': True,
 'shuffle': None,
 'sigma': 0.0,
 'spot_tensorboard_path': 'runs/spot_logs/04_DE__maans14_2024-04-22_00-18-10',
 'spot_writer': <torch.utils.tensorboard.writer.SummaryWriter object at 0x3c86e6f50>,
 'target_column': None,
 'target_type': None,
 'task': None,
 'test': None,
 'test_seed': 1234,
 'test_size': 0.4,
 'tolerance_x': 0,
 'train': None,
 'upper': array([10, 15]),
 'var_name': None,
 'var_type': ['num'],
 'verbosity': 0,
 'weight_coeff': 0.0,
 'weights': 1.0,
 'weights_entry': None}
min y: 0.3993792812618935
x0: 3.150848989866496
x1: 2.3006645011798197

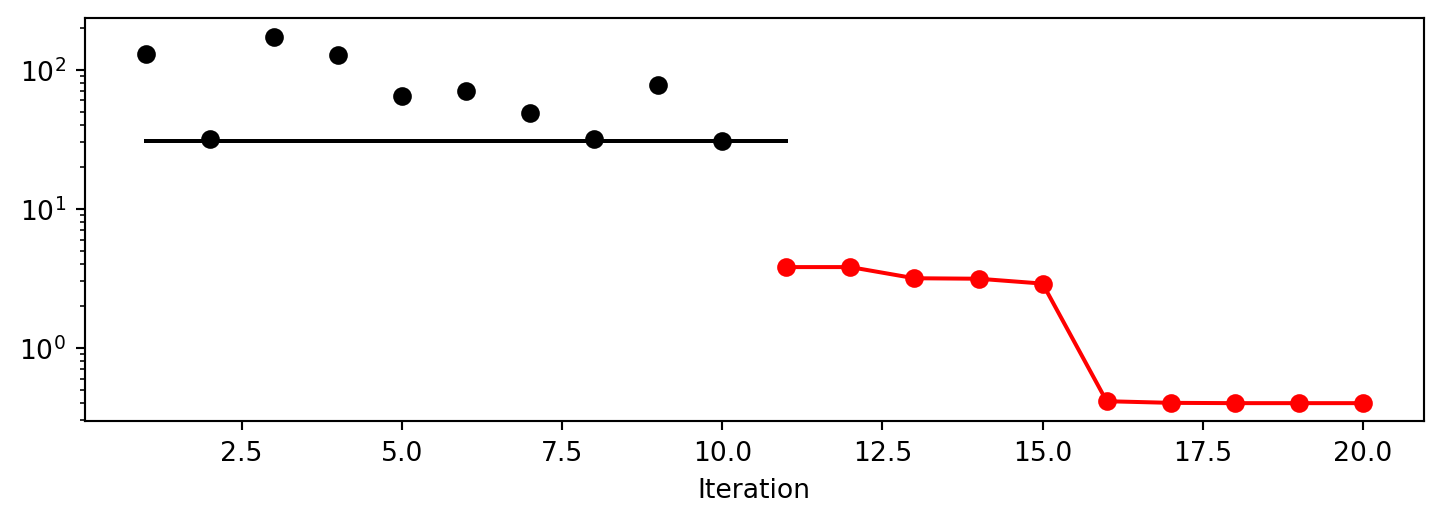
4.5.5 Performance Comparison

Compare the performance and run time of the 5 different optimizers:

differential_evolution
dual_annealing
direct
shgo
basinhopping.

The Branin function has three global minima:

\(f(x) = 0.397887\) at
- \((-\pi, 12.275)\),
- \((\pi, 2.275)\), and
- \((9.42478, 2.475)\).
Which optima are found by the optimizers?
Does the seed argument in fun = analytical(seed=123).fun_branin change this behavior?

4.6 Jupyter Notebook

Note

The Jupyter-Notebook of this lecture is available on GitHub in the Hyperparameter-Tuning-Cookbook Repository

4.1 The Objective Function Branin

4.2 The Optimizer

4.2.1 TensorBoard

4.3 Print the Results

4.4 Show the Progress

4.5 Exercises

4.5.1 dual_annealing

4.5.2 direct

4.5.3 shgo

4.5.4 basinhopping

4.5.5 Performance Comparison

4.6 Jupyter Notebook

4.5.1 `dual_annealing`

4.5.2 `direct`

4.5.3 `shgo`

4.5.4 `basinhopping`