import numpy as np
import matplotlib.pyplot as plt
from numpy import (exp, multiply, eye, linspace, spacing, sqrt)
from numpy.linalg import cholesky, solve
from scipy.spatial.distance import squareform, pdist, cdist
from scipy.optimize import minimize # Für die Optimierung
class KrigingRegressor:
"""Ein Kriging-Regressionsmodell mit Hyperparameter-Optimierung.
Attributes:
initial_theta (float): Startwert für den Aktivitätsparameter Theta.
bounds (list): Liste von Tupeln für die Grenzen der Hyperparameter-Optimierung.
opt_theta_ (float): Optimierter Theta-Wert nach dem Fitting.
X_train_ (array): Trainings-Eingabedaten.
y_train_ (array): Trainings-Zielwerte.
U_ (array): Cholesky-Zerlegung der Korrelationsmatrix.
mu_hat_ (float): Geschätzter Mittelwert.
"""
def __init__(self, initial_theta=1.0, bounds=[(0.001, 100.0)]):
self.initial_theta = initial_theta
self.bounds = bounds
def _build_Psi(self, X, theta, eps=sqrt(spacing(1))):
"""Berechnet die Korrelationsmatrix Psi."""
if not isinstance(theta, np.ndarray) or theta.ndim == 0:
theta = np.array([theta])
D = squareform(pdist(X, metric='sqeuclidean', w=theta))
Psi = exp(-D)
Psi += multiply(eye(X.shape[0]), eps)
return Psi
def _build_psi(self, X_train, x_predict, theta):
"""Berechnet den Korrelationsvektor psi."""
if not isinstance(theta, np.ndarray) or theta.ndim == 0:
theta = np.array([theta])
D = cdist(x_predict, X_train, metric='sqeuclidean', w=theta)
psi = exp(-D)
return psi.T
def _neg_log_likelihood(self, params, X_train, y_train):
"""Berechnet die negative konzentrierte Log-Likelihood."""
theta = params
n = X_train.shape[0]
try:
Psi = self._build_Psi(X_train, theta)
U = cholesky(Psi).T
except np.linalg.LinAlgError:
return 1e15
one = np.ones(n).reshape(-1, 1)
# Berechne mu_hat (MLE des Mittelwerts)
Psi_inv_y = solve(U, solve(U.T, y_train))
Psi_inv_one = solve(U, solve(U.T, one))
mu_hat = (one.T @ Psi_inv_y) / (one.T @ Psi_inv_one)
mu_hat = mu_hat.item()
# Berechne sigma_hat_sq (MLE der Prozessvarianz)
y_minus_mu_one = y_train - one * mu_hat
sigma_hat_sq = (y_minus_mu_one.T @ Psi_inv_y) / n
sigma_hat_sq = sigma_hat_sq.item()
if sigma_hat_sq < 1e-10:
return 1e15
# Berechne negative konzentrierte Log-Likelihood
log_det_Psi = 2 * np.sum(np.log(np.diag(U.T)))
nll = 0.5 * (n * np.log(sigma_hat_sq) + log_det_Psi)
return nll
def fit(self, X, y):
"""Fit das Kriging-Modell an die Trainingsdaten.
// ...existing docstring...
"""
self.X_train_ = X
self.y_train_ = y.reshape(-1, 1)
# Optimierung der Hyperparameter
initial_theta = np.array([self.initial_theta])
result = minimize(self._neg_log_likelihood,
initial_theta,
args=(self.X_train_, self.y_train_),
method='L-BFGS-B',
bounds=self.bounds)
self.opt_theta_ = result.x
# Berechne optimale Parameter für Vorhersagen
Psi_opt = self._build_Psi(self.X_train_, self.opt_theta_)
self.U_ = cholesky(Psi_opt).T
n_train = self.X_train_.shape[0]
one = np.ones(n_train).reshape(-1, 1)
self.mu_hat_ = (one.T @ solve(self.U_, solve(self.U_.T, self.y_train_))) / \
(one.T @ solve(self.U_, solve(self.U_.T, one)))
self.mu_hat_ = self.mu_hat_.item()
return self
def predict(self, X):
"""Vorhersage für neue Datenpunkte.
Args:
X (array-like): Eingabedaten für Vorhersage der Form (n_samples, n_features)
Returns:
array: Vorhergesagte Werte
"""
n_train = self.X_train_.shape[0]
one = np.ones(n_train).reshape(-1, 1)
# Fix: Use self._build_psi instead of build_psi
psi = self._build_psi(self.X_train_, X, self.opt_theta_)
return self.mu_hat_ * np.ones(X.shape[0]).reshape(-1, 1) + \
psi.T @ solve(self.U_, solve(self.U_.T,
self.y_train_ - one * self.mu_hat_))67 Lernmodul: Erweiterung des Kriging-Modells zu einer Klasse (Python Code)
def plot_kriging_results(X_train, y_train, X_test, y_test, y_pred, theta, figsize=(10, 6)):
"""Visualisiert die Kriging-Vorhersage im Vergleich zur wahren Funktion.
Args:
X_train (array-like): Trainings-Eingabedaten
y_train (array-like): Trainings-Zielwerte
X_test (array-like): Test-Eingabedaten
y_test (array-like): Wahre Werte zum Vergleich
y_pred (array-like): Vorhersagewerte des Modells
theta (float): Optimierter Theta-Parameter
figsize (tuple, optional): Größe der Abbildung. Default ist (10, 6).
"""
plt.figure(figsize=figsize)
# Sortiere Test-Daten nach X-Werten für eine glatte Linie
sort_idx_test = np.argsort(X_test.ravel())
X_test_sorted = X_test[sort_idx_test]
y_test_sorted = y_test[sort_idx_test]
y_pred_sorted = y_pred[sort_idx_test]
# Wahre Funktion
plt.plot(X_test_sorted, y_test_sorted, color="grey", linestyle='--',
label="Wahre Sinusfunktion")
# Trainingspunkte
n_train = len(X_train)
plt.plot(X_train, y_train, "bo", markersize=8,
label=f"Messpunkte ({n_train} Punkte)")
# Vorhersage
plt.plot(X_test_sorted, y_pred_sorted, color="orange",
label=f"Kriging-Vorhersage (Theta={theta:.2f})")
# Plot-Eigenschaften
plt.title(f"Kriging-Vorhersage mit {n_train} Trainings-Punkten\n" +
f"Optimierter Aktivitätsparameter Theta={theta:.2f}")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc='upper right')
plt.grid(True)
plt.show()67.1 Ein erste Beispielverwendung:
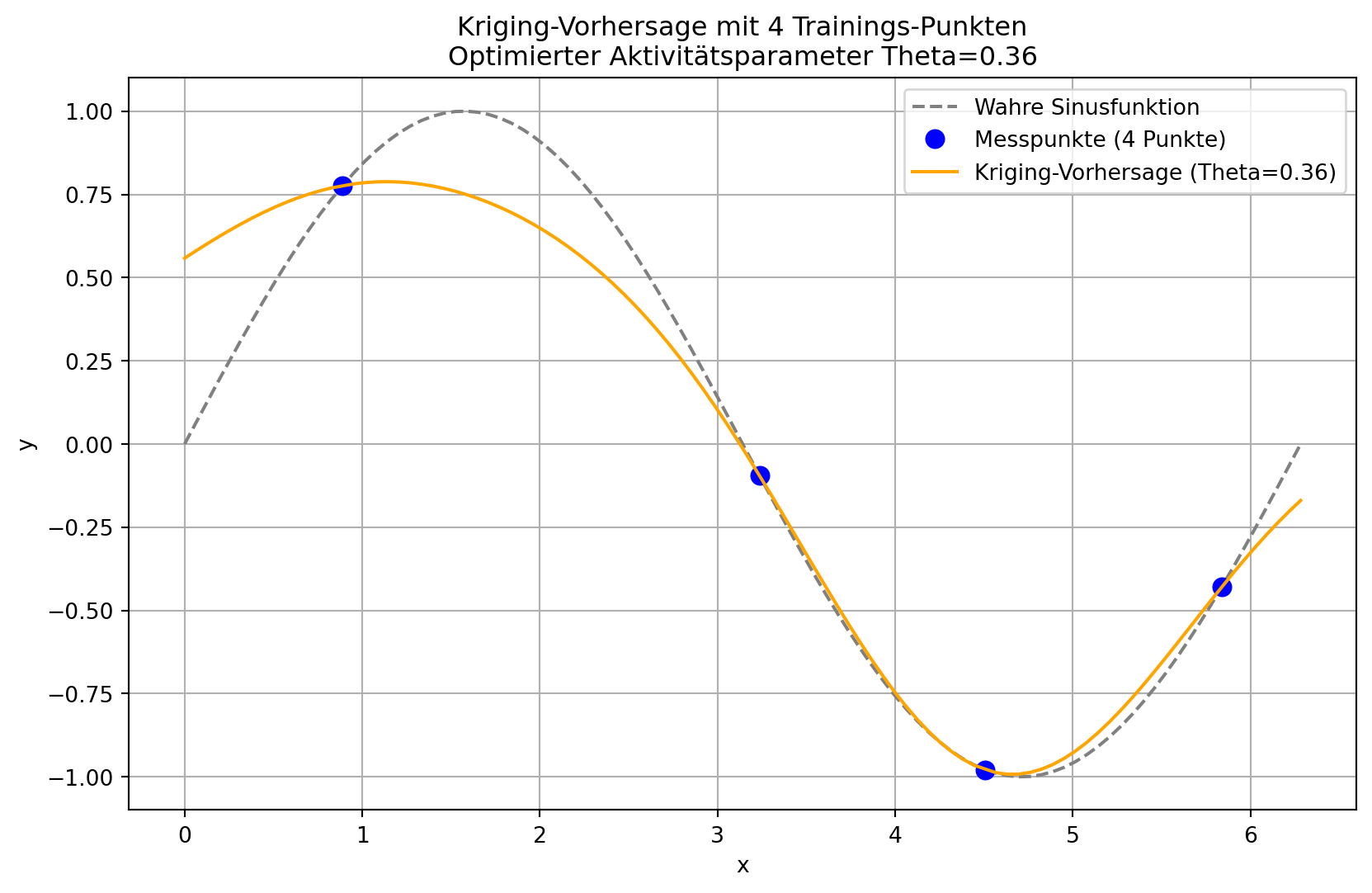
# Generiere Trainingsdaten
n_train = 4
X_train = np.linspace(0, 2 * np.pi, n_train, endpoint=False).reshape(-1, 1)
y_train = np.sin(X_train)
# Erstelle und trainiere das Modell
model = KrigingRegressor(initial_theta=1.0)
model.fit(X_train, y_train)
# Generiere Testdaten
X_test = np.linspace(0, 2 * np.pi, 100, endpoint=True).reshape(-1, 1)
y_test = np.sin(X_test)
# Mache Vorhersagen
y_pred = model.predict(X_test)
# Visualisiere die Ergebnisse
plot_kriging_results(
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
y_pred=y_pred,
theta=model.opt_theta_[0]
)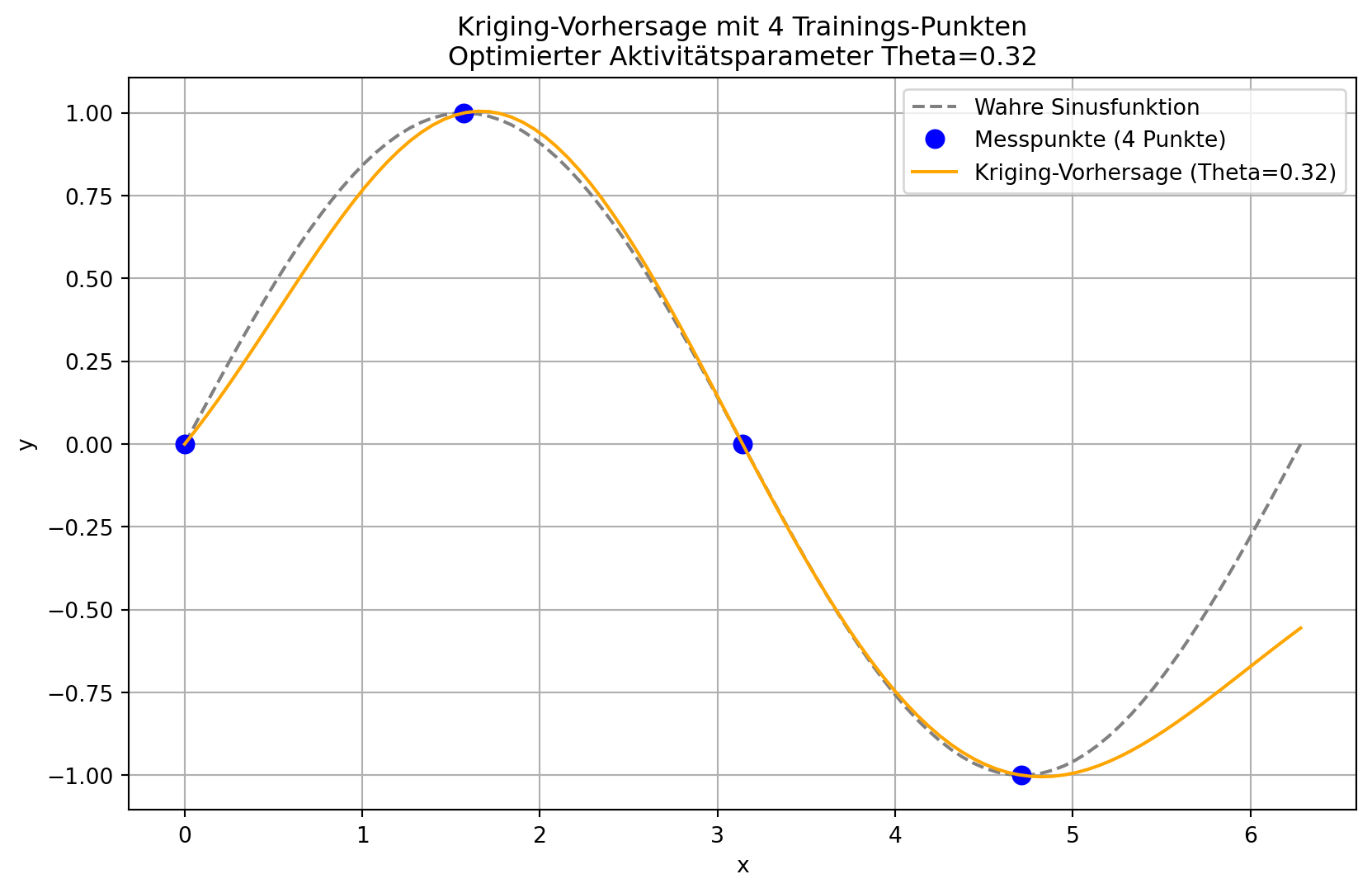
67.2 Ein zweites Beispiel mit train_test_split:
from sklearn.model_selection import train_test_split
import numpy as np
# Generate sample data
n_samples = 100
X = np.linspace(0, 2 * np.pi, n_samples).reshape(-1, 1)
y = np.sin(X)
# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=96, random_state=42)
# Fit model
model = KrigingRegressor(initial_theta=1)
model.fit(X_train, y_train)
# Make predictions
y_pred = model.predict(X_test)
# Visualize results
plot_kriging_results(
X_train=X_train,
y_train=y_train,
X_test=X_test,
y_test=y_test,
y_pred=y_pred,
theta=model.opt_theta_[0]
)