import numpy as np
import matplotlib.pyplot as plt
from numpy import (exp, multiply, eye, linspace, spacing, sqrt)
from numpy.linalg import cholesky, solve
from scipy.spatial.distance import squareform, pdist, cdist
from scipy.optimize import minimize # Für die Optimierung66 Lernmodul: Erweiterung des Kriging-Modells: Numerische Optimierung der Hyperparameter
66.1 Einleitung
Das vorhergehende Lernmodul hat die konzeptionellen Grundlagen und die mathematische Architektur von Kriging-Modellen vorgestellt, illustriert am Beispiel der Sinusfunktion. In dieser Einführung wurde der Aktivitätsparameter \(\theta\) aus Gründen der Einfachheit auf einen festen Wert (1.0) gesetzt. In realen Anwendungen ist es jedoch entscheidend, diese Parameter optimal aus den vorliegenden Daten zu bestimmen, um die bestmögliche Modellgüte zu erzielen.
Dieses Dokument baut auf dem bestehenden Wissen auf und erläutert, wie die Kriging-Hyperparameter, insbesondere der Aktivitätsparameter \(\theta\), numerisch optimiert werden können. Wir werden uns auf die Maximierung der sogenannten “konzentrierten Log-Likelihood-Funktion” konzentrieren, einem gängigen Ansatz zur Parameterschätzung in Kriging-Modellen. Die gezeigte Python-Code-Erweiterung des Sinusfunktions-Beispiels verdeutlicht die praktische Umsetzung.
66.2 Kriging-Hyperparameter: Theta (\(\vec{\theta}\)) und p (\(\vec{p}\))
Im Kriging-Modell steuern zwei wichtige Vektoren von Hyperparametern die Form und die Eigenschaften der Korrelationsfunktion:
- Aktivitätsparameter \(\vec{\theta} = (\theta_1, \theta_2, \ldots, \theta_k)^T\): Dieser Vektor regelt, wie schnell die Korrelation zwischen zwei Punkten mit zunehmendem Abstand in jeder Dimension abfällt. Ein großer Wert für \(\theta_j\) in einer Dimension \(j\) bedeutet, dass die Funktion in dieser Dimension sehr “aktiv” ist oder sich schnell ändert, und somit nur Punkte in unmittelbarer Nähe stark korrelieren. Dies ermöglicht eine automatische Relevanzbestimmung, bei der wichtige Variablen durch höhere \(\theta\)-Werte identifiziert werden können.
- Glattheitsparameter \(\vec{p} = (p_1, p_2, \ldots, p_k)^T\): Dieser Vektor beeinflusst die Glattheit der Vorhersagefunktion in jeder Dimension. Üblicherweise liegen die Werte für \(p_j\) zwischen 1 und 2. Im vorherigen Lernmodul wurde implizit \(p_j=2\) verwendet (durch die “sqeuclidean”-Distanzmetrik), was zu unendlich differenzierbaren, sehr glatten Funktionen führt. Eine Optimierung von \(\vec{p}\) ist möglich, wird aber in diesem Beispiel aus Gründen der Komplexität ausgeklammert, da \(p_j=2\) oft als Standard für glatte Funktionen angenommen wird.
66.3 Die Notwendigkeit der Optimierung: Die konzentrierte Log-Likelihood
Um die optimalen Werte für \(\vec{\theta}\) (und \(\vec{p}\)) zu finden, wird häufig die Maximum-Likelihood-Schätzung (MLE) verwendet. Die Grundidee der MLE besteht darin, diejenigen Parameterwerte zu finden, die die Wahrscheinlichkeit maximieren, die tatsächlich beobachteten Daten zu erhalten.
Die zu maximierende Funktion ist die Log-Likelihood-Funktion. Für gegebene \(\vec{\theta}\) und \(\vec{p}\) (und somit eine feste Korrelationsmatrix \(\Psi\)) können die Schätzer für den globalen Mittelwert \(\hat{\mu}\) und die Prozessvarianz \(\hat{\sigma}^2\) analytisch abgeleitet werden. Durch Einsetzen dieser Schätzer in die Log-Likelihood-Funktion erhalten wir die sogenannte konzentrierte Log-Likelihood-Funktion:
\[ \ln(L) \approx - \frac{n}{2} \ln(\hat{\sigma}^2) - \frac{1}{2} \ln |\vec{\Psi}| \]
Hierbei ist:
- \(n\): Die Anzahl der Beobachtungspunkte.
- \(\hat{\sigma}^2\): Der Maximum-Likelihood-Schätzer der Prozessvarianz.
- \(|\vec{\Psi}|\): Die Determinante der Korrelationsmatrix \(\vec{\Psi}\).
Die direkte Maximierung dieser Funktion ist mathematisch schwierig, da sie bezüglich \(\vec{\theta}\) und \(\vec{p}\) nicht analytisch differenzierbar ist. Daher wird eine numerische Optimierung eingesetzt, um die Parameter zu finden, die die konzentrierte Log-Likelihood maximieren.
66.4 Numerische Optimierungsalgorithmen
Für die numerische Optimierung der Parameter \(\vec{\theta}\) und \(\vec{p}\) können verschiedene Algorithmen verwendet werden, darunter:
- Nelder-Mead-Simplex-Verfahren
- Konjugierte Gradienten-Verfahren
- Simulated Annealing
- Differential Evolution
Die scipy.optimize-Bibliothek in Python bietet eine umfassende Sammlung solcher Optimierungsfunktionen. Da die meisten Optimierungsalgorithmen in scipy.optimize auf Minimierung ausgelegt sind, wird die negative konzentrierte Log-Likelihood-Funktion als Optimierungsziel verwendet.
Ein wichtiger numerischer Aspekt bei der Berechnung der Log-Likelihood ist die Determinante von \(\Psi\). Für schlecht konditionierte Matrizen kann \(|\Psi|\) gegen Null gehen, was zu numerischer Instabilität führen kann. Um dies zu vermeiden, wird der Logarithmus der Determinante \(\ln(|\Psi|)\) stabiler berechnet, indem man die Cholesky-Zerlegung \(\Psi = L L^T\) nutzt und dann \(\ln(|\Psi|) = 2 \sum_{i=1}^{n} \ln(L_{ii})\) berechnet.
Für die Suche nach \(\theta\) ist es sinnvoll, Suchbereiche auf einer logarithmischen Skala zu definieren, typischerweise von \(10^{-3}\) bis \(10^2\). Es ist auch ratsam, die Eingabedaten auf den Bereich zwischen Null und Eins zu skalieren, um die Konsistenz der \(\theta\)-Werte über verschiedene Probleme hinweg zu gewährleisten.
66.5 Erweiterung des Sinusfunktions-Beispiels mit Hyperparameter-Optimierung
Wir erweitern nun den Beispielcode aus dem “Lernmodul: Eine Einführung in Kriging” (Kriging-Anpassung an eine Sinusfunktion mit 8 Punkten), um den Aktivitätsparameter \(\theta\) numerisch zu optimieren.
Die Hauptänderung besteht in der Definition einer neuen Zielfunktion, neg_log_likelihood, die von scipy.optimize.minimize minimiert wird. Diese Funktion nimmt die zu optimierenden Parameter (hier theta) entgegen und berechnet die negative konzentrierte Log-Likelihood basierend auf den Trainingsdaten.
66.5.1 Kriging-Basisfunktionen (Definition der Korrelation)
Der Kernel von Kriging verwendet eine spezialisierte Basisfunktion für die Korrelation: \[ \psi(x^{(i)}, x) = \exp(- \sum_{j=1}^k \theta_j |x_j^{(i)} - x_j|^{p_j}). \]
Für dieses 1D-Beispiel (\(k=1\)) und mit \(p_j=2\) (quadratische euklidische Distanz implizit durch pdist-Nutzung) und \(\theta_j = \theta\) (ein einzelner Wert) vereinfacht es sich.
def build_Psi(X, theta, eps=sqrt(spacing(1))):
"""
Berechnet die Korrelationsmatrix Psi basierend auf paarweisen
quadratischen euklidischen Distanzen zwischen Eingabelokationen,
skaliert mit theta.
Fügt ein kleines Epsilon zur Diagonalen für numerische Stabilität
hinzu (Nugget-Effekt).
Hinweis: p_j ist implizit 2 aufgrund der 'sqeuclidean'-Metrik.
"""
# Sicherstellen, dass theta ein 1D-Array für das 'w'-Argument
# von cdist/pdist ist
if not isinstance(theta, np.ndarray) or theta.ndim == 0:
theta = np.array([theta])
D = squareform(pdist(X, metric='sqeuclidean', w=theta))
Psi = exp(-D)
# Ein kleiner Wert wird zur Diagonalen hinzugefügt für
# numerische Stabilität (Nugget)
# Korrektur: X.shape für die Anzahl der Zeilen der
# Identitätsmatrix
Psi += multiply(eye(X.shape[0]), eps)
return Psi
def build_psi(X_train, x_predict, theta):
"""
Berechnet den Korrelationsvektor (oder Matrix) psi zwischen
neuen Vorhersageorten und Trainingsdatenlokationen.
"""
# Sicherstellen, dass theta ein 1D-Array für das 'w'-Argument
# von cdist/pdist ist
if not isinstance(theta, np.ndarray) or theta.ndim == 0:
theta = np.array([theta])
D = cdist(x_predict, X_train, metric='sqeuclidean', w=theta)
psi = exp(-D)
return psi.T
# Transponieren, um konsistent mit der Literatur zu sein
# (n x m oder n x 1)66.5.2 Zielfunktion für die Hyperparameter-Optimierung (Negative Log-Likelihood)
def neg_log_likelihood(params, X_train, y_train):
"""
Berechnet die negative konzentrierte Log-Likelihood für das Kriging-Modell.
params: ein 1D-Numpy-Array, wobei params theta ist.
(Falls auch p optimiert würde, wäre es params usw.)
X_train: (n, k)-Matrix der Trainings-Eingabelokationen
y_train: (n, 1)-Vektor der Trainings-Ausgabewerte
"""
theta = params
# Für dieses Beispiel ist p implizit auf 2 festgelegt
# (durch 'sqeuclidean' in build_Psi).
# Falls p optimiert würde, müsste es hier aus 'params' extrahiert
# und an build_Psi übergeben werden
n = X_train.shape[0]
# 1. Korrelationsmatrix Psi aufbauen
Psi = build_Psi(X_train, theta)
# 2. mu_hat berechnen (MLE des Mittelwerts)
# Verwendung der Cholesky-Zerlegung für stabile Inversion
try:
# numpy.cholesky gibt L (untere Dreiecksmatrix) zurück,
# daher transponieren für U (obere)
U = cholesky(Psi).T
except np.linalg.LinAlgError:
# Bei Fehlern (z.B. wenn Psi nicht positiv definit ist,
# durch schlechte theta-Werte)
# einen sehr großen Wert zurückgeben, um diese Parameter zu bestrafen
return 1e15
one = np.ones(n).reshape(-1, 1)
# Stabile Berechnung von Psi_inv @ y und Psi_inv @ one
Psi_inv_y = solve(U, solve(U.T, y_train))
Psi_inv_one = solve(U, solve(U.T, one))
# Berechnung von mu_hat
mu_hat = (one.T @ Psi_inv_y) / (one.T @ Psi_inv_one)
mu_hat = mu_hat.item() # Skalaren Wert extrahieren
# 3. sigma_hat_sq berechnen (MLE der Prozessvarianz)
y_minus_mu_one = y_train - one * mu_hat
# Korrekte Berechnung: (y-1*mu_hat).T @ Psi_inv @ (y-1*mu_hat) / n
sigma_hat_sq = (y_minus_mu_one.T @ \
solve(U, solve(U.T, y_minus_mu_one))) / n
sigma_hat_sq = sigma_hat_sq.item()
if sigma_hat_sq < 1e-10: # Sicherstellen, dass sigma_hat_sq
# nicht-negativ und nicht zu klein ist
return 1e15 # Sehr großen Wert zurückgeben zur Bestrafung
# 4. Log-Determinante von Psi mittels Cholesky-Zerlegung für
# Stabilität berechnen.
# ln(|Psi|) = 2 * Summe(ln(L_ii)) wobei L die untere
# Dreiecksmatrix der Cholesky-Zerlegung ist
log_det_Psi = 2 * np.sum(np.log(np.diag(U.T))) # U.T ist L
# 5. Negative konzentrierte Log-Likelihood berechnen
# ln(L) = - (n/2) * ln(sigma_hat_sq) - (1/2) * ln(|Psi|)
# Zu minimieren ist -ln(L)
nll = 0.5 * n * np.log(sigma_hat_sq) + 0.5 * log_det_Psi
return nll66.5.3 Datenpunkte für das Sinusfunktions-Beispiel
Das Beispiel verwendet eine 1D-Sinusfunktion, gemessen an n_train gleichmäßig verteilten x-Lokationen.
n_train = 4 # Anzahl der Stichprobenlokationen
X_train = np.linspace(0, 2 * np.pi, n_train,\
endpoint=False).reshape(-1, 1)
y_train = np.sin(X_train) # Zugehörige y-Werte (Sinus von x)
# --- Originale Vorhersage-Einrichtung (festes theta=1.0) ---
theta_fixed = np.array([1.0])
Psi_fixed = build_Psi(X_train, theta_fixed)
U_fixed = cholesky(Psi_fixed).T
one_fixed = np.ones(n_train).reshape(-1, 1)
mu_hat_fixed = (one_fixed.T @ solve(U_fixed,\
solve(U_fixed.T, y_train)))\
/ (one_fixed.T @ solve(U_fixed,\
solve(U_fixed.T, one_fixed)))
mu_hat_fixed = mu_hat_fixed.item()
m_predict = 100 # Anzahl der neuen Lokationen für die Vorhersage
x_predict = np.linspace(0, 2 * np.pi, m_predict,\
endpoint=True).reshape(-1, 1)
psi_fixed = build_psi(X_train, x_predict, theta_fixed)
f_predict_fixed = mu_hat_fixed * np.ones(m_predict).reshape(-1, 1) + \
psi_fixed.T @ solve(U_fixed, solve(U_fixed.T,\
y_train - one_fixed * mu_hat_fixed))66.5.4 Optimierung von Theta
initial_theta_guess = np.array([1.0]) # Startwert für Theta
# Suchbereiche für Theta (z.B. von 1e-3 bis 1e2 auf linearer Skala)
# SciPy minimize erwartet Suchbereiche als Tupel von (min, max)
# für jeden Parameter
bounds = [(0.001, 100.0)] # Für Theta
print("\n--- Starte Hyperparameter-Optimierung für Theta ---")
# 'L-BFGS-B' wird verwendet, da es Beschränkungen (bounds) unterstützt
# und gut für kontinuierliche Optimierung ist.
result = minimize(neg_log_likelihood, initial_theta_guess,\
args=(X_train, y_train),
method='L-BFGS-B', bounds=bounds)
opt_theta = result.x
opt_nll = result.fun
print(f"Optimierung erfolgreich: {result.success}")
# Extract the first element if it's a single value
print(f"Optimales Theta: {opt_theta[0]:.4f}")
print(f"Minimaler Negativer Log-Likelihood: {opt_nll:.4f}")
--- Starte Hyperparameter-Optimierung für Theta ---
Optimierung erfolgreich: True
Optimales Theta: 0.3157
Minimaler Negativer Log-Likelihood: -1.476766.5.5 Vorhersage mit optimiertem Theta
Psi_opt = build_Psi(X_train, opt_theta)
U_opt = cholesky(Psi_opt).T
one_opt = np.ones(n_train).reshape(-1, 1)
mu_hat_opt = (one_opt.T @ solve(U_opt, solve(U_opt.T, y_train))) / \
(one_opt.T @ solve(U_opt, solve(U_opt.T, one_opt)))
mu_hat_opt = mu_hat_opt.item()
psi_opt = build_psi(X_train, x_predict, opt_theta)
f_predict_opt = mu_hat_opt * np.ones(m_predict).reshape(-1, 1) + \
psi_opt.T @ solve(U_opt, solve(U_opt.T, y_train\
- one_opt * mu_hat_opt))66.5.6 Visualisierung der Ergebnisse
plt.figure(figsize=(10, 6))
plt.plot(x_predict, np.sin(x_predict), color="grey", linestyle='--',\
label="Wahre Sinusfunktion")
plt.plot(X_train, y_train, "bo", markersize=8,\
label=f"Messpunkte ({n_train} Punkte)")
plt.plot(x_predict, f_predict_fixed, color="red", linestyle=':',\
label=f"Kriging-Vorhersage (Fixes Theta={theta_fixed[0]:.1f})")
plt.plot(x_predict, f_predict_opt, color="orange",\
label=f"Kriging-Vorhersage (Optimiertes Theta={opt_theta[0]:.2f})")
plt.title(f"Kriging-Vorhersage der Sinusfunktion mit {n_train} Punkten\
\nOptimierung des Aktivitätsparameters Theta")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc='upper right')
plt.grid(True)
plt.show()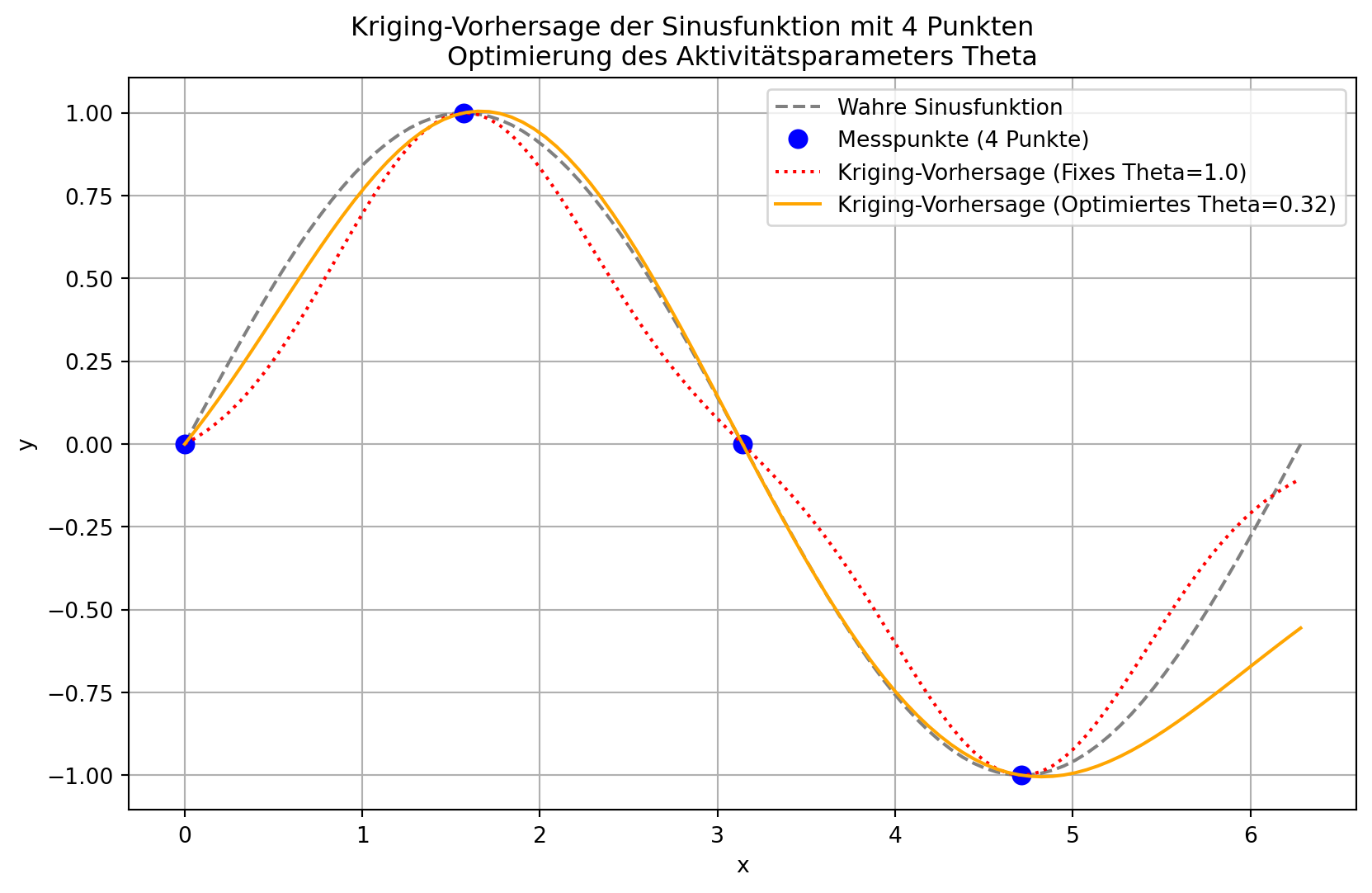
66.5.7 6. Ergebnisse und Diskussion
Die grafische Darstellung der Ergebnisse zeigt die Verbesserung der Kriging-Vorhersage nach der Optimierung des Aktivitätsparameters \(\theta\). Die Kurve, die mit dem optimierten \(\theta\)-Wert generiert wurde, passt sich in der Regel besser an die Trainingsdaten an und bildet den wahren Funktionsverlauf präziser ab, als dies mit einem willkürlich gewählten \(\theta\)-Wert der Fall wäre. Der Optimierungsalgorithmus findet den \(\theta\)-Wert, der die Korrelationsstruktur der Daten am besten erklärt und somit ein “realistischeres” Modell der zugrunde liegenden Funktion liefert.
In diesem 1D-Beispiel ist der Unterschied möglicherweise subtil, aber in höherdimensionalen Problemen, wo Variablen unterschiedliche “Aktivitäten” aufweisen, ist die automatische Bestimmung von \(\vec{\theta}\) entscheidend für die Modellgenauigkeit und die Identifizierung wichtiger Input-Variablen.
66.5.8 7. Fazit und Ausblick
Dieses Lernmodul hat gezeigt, wie die Maximum-Likelihood-Schätzung in Verbindung mit numerischen Optimierungsverfahren genutzt werden kann, um die Hyperparameter eines Kriging-Modells optimal an die Daten anzupassen. Die Optimierung der konzentrierten Log-Likelihood-Funktion ist ein Standardansatz, der die Robustheit und Genauigkeit von Kriging-Modellen erheblich verbessert.
Für fortgeschrittenere Anwendungen könnten weitere Schritte unternommen werden:
- Optimierung von \(\vec{p}\): Der Glattheitsparameter \(\vec{p}\) könnte ebenfalls in den Optimierungsprozess einbezogen werden, um noch flexiblere Anpassungen zu ermöglichen.
- Kriging-Regression für verrauschte Daten: Falls die Trainingsdaten Rauschen enthalten (z.B. aus physikalischen Experimenten), kann ein zusätzlicher “Nugget”-Parameter \(\lambda\) in der Korrelationsmatrix optimiert werden. Dies transformiert das interpolierende Kriging in ein regressives Kriging, das Rauschen explizit modelliert und eine glattere Vorhersagekurve liefert.
- Aktives Lernen und Expected Improvement (EI): Kriging-Modelle liefern nicht nur Vorhersagen, sondern auch Unsicherheitsschätzungen (Varianz) an jedem Punkt. Dies ermöglicht den Einsatz von “Infill-Kriterien” wie Expected Improvement (EI), um den nächsten vielversprechendsten Punkt für eine Funktionsauswertung intelligent auszuwählen, was besonders bei teuren Simulationen effizient ist.
- Co-Kriging (Multi-Fidelity-Modellierung): Wenn Daten aus verschiedenen Quellen mit unterschiedlicher Genauigkeit und Kosten verfügbar sind, kann Co-Kriging (auch Multi-Fidelity-Modellierung genannt) diese Daten integrieren, um genauere Modelle zu erstellen.
Diese erweiterten Konzepte bilden die Grundlage für robuste und effiziente Optimierungsprozesse in vielen technischen und wissenschaftlichen Disziplinen.
66.6 Zusatzmaterialien
- Eine interaktive Webseite zum Thema Kriging: Optimierung der Hyperparameter ist hier zu finden: Kriging Interaktiv.
- Das Jupyter-Notebook für dieses Lernmodul ist auf GitHub im Hyperparameter-Tuning-Cookbook Repository verfügbar.