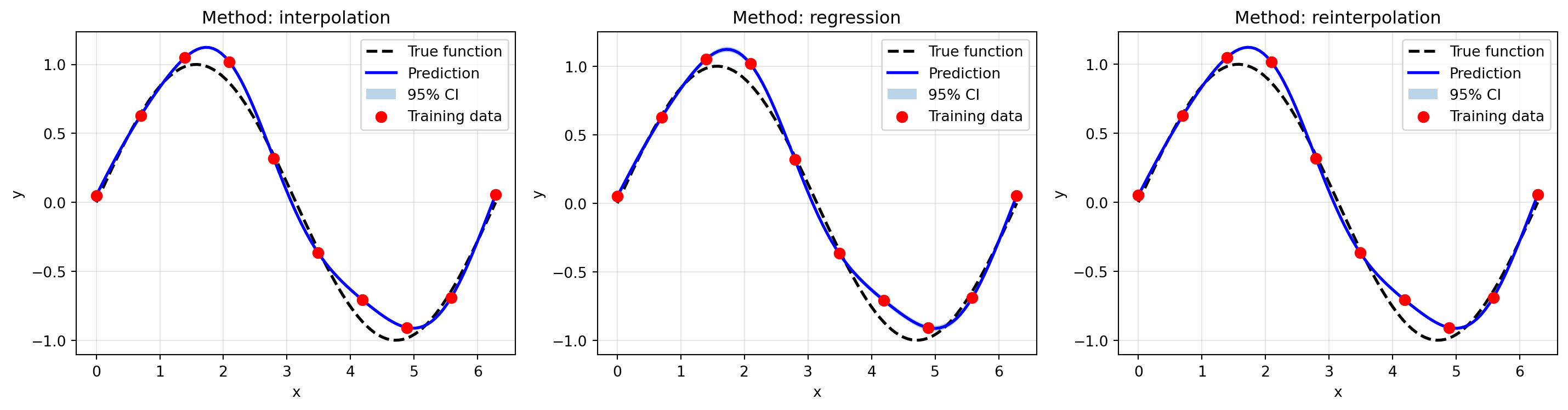
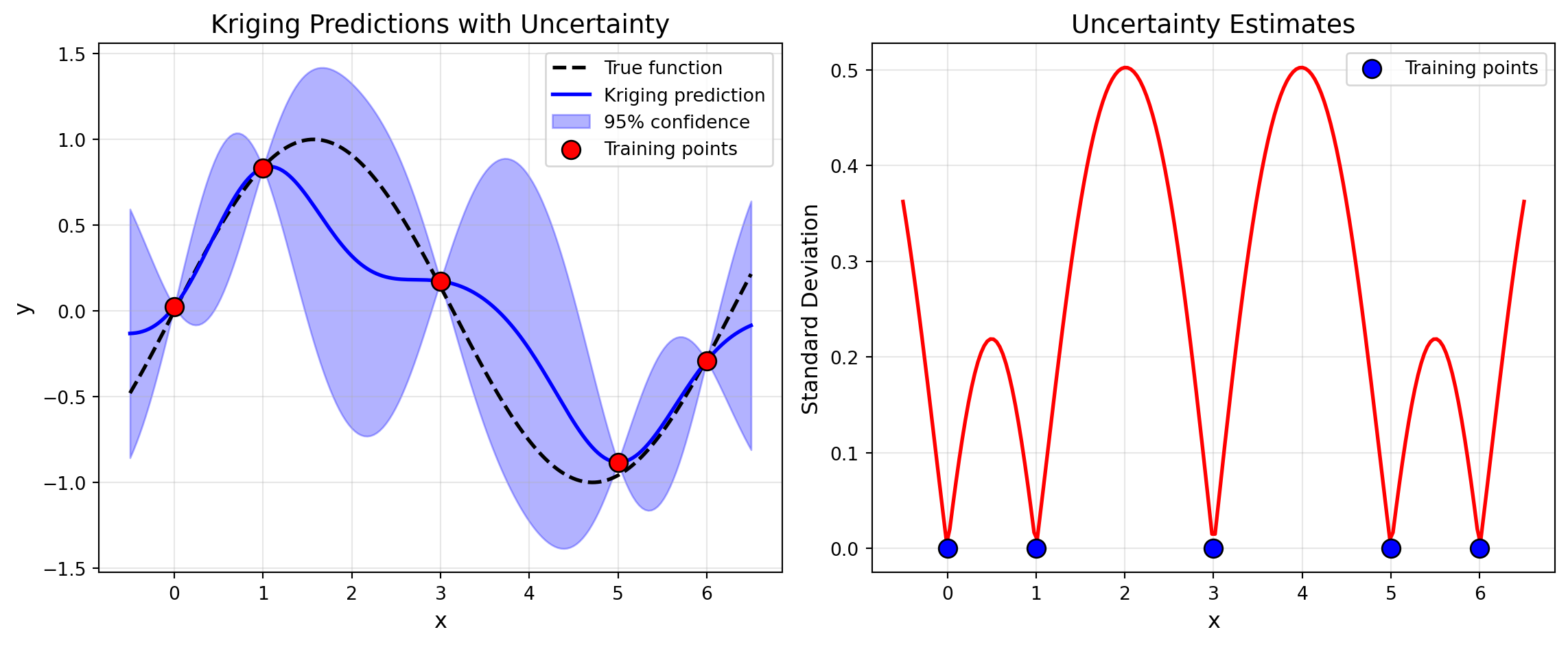
import numpy as np
from spotoptim.surrogate import Kriging
import matplotlib.pyplot as plt
# 1D example for visualization
np.random.seed(42)
X_train = np.array([[0.0], [1.0], [3.0], [5.0], [6.0]])
y_train = np.sin(X_train.ravel()) + 0.05 * np.random.randn(5)
# Fit Kriging model
model = Kriging(method='regression', seed=42, model_fun_evals=50)
model.fit(X_train, y_train)
# Dense test points
X_test = np.linspace(-0.5, 6.5, 200).reshape(-1, 1)
y_pred, y_std = model.predict(X_test, return_std=True)
# True function
y_true = np.sin(X_test.ravel())
# Plot
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(X_test, y_true, 'k--', label='True function', linewidth=2)
plt.plot(X_test, y_pred, 'b-', label='Kriging prediction', linewidth=2)
plt.fill_between(X_test.ravel(),
y_pred - 2*y_std,
y_pred + 2*y_std,
alpha=0.3, color='blue', label='95% confidence')
plt.scatter(X_train, y_train, c='red', s=100, zorder=5,
edgecolors='black', label='Training points')
plt.xlabel('x', fontsize=12)
plt.ylabel('y', fontsize=12)
plt.title('Kriging Predictions with Uncertainty', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.subplot(1, 2, 2)
plt.plot(X_test, y_std, 'r-', linewidth=2)
plt.scatter(X_train, np.zeros_like(X_train), c='blue', s=100,
zorder=5, edgecolors='black', label='Training points')
plt.xlabel('x', fontsize=12)
plt.ylabel('Standard Deviation', fontsize=12)
plt.title('Uncertainty Estimates', fontsize=14)
plt.legend()
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
print("Key observations:")
print("- Uncertainty is low near training points")
print("- Uncertainty is high far from training data")
print("- This guides acquisition functions (e.g., EI exploits low uncertainty)")